分析高中数学不等式易错题型及解题技巧

李静

摘 要：文章以分析高中数学不等式易错题型及解题技巧为主要内容，以当下高中数学新课程标准需求为主要依据，从和线性规划结合问题、高次不等式的解答方法、不等式等价转化问题、含参不等式问题、绝对值不等式问题、不等式恒成立问题这几方面进行深入探讨和分析，其目的在于更好地解答高中数学不等式易错题，使得学生掌握一定技巧，旨在为相关研究提供参考资料。

关键词：高中数学知识;不等式问题;易错题;解题技巧

中图分类号：G633.6 文献标识码：A 文章编号：2095-624X（2020）27-0081-02

一、逐渐引入不等式概念

不等式概念中，包含了数学思考，但多数教师只是根据教学参考书以及大纲来安排教学，直接进入不等式的内容讲解。笔者认为在引入不等式概念时一定要逐渐引进。在接触不等式知识前，学生习惯用等号来连接式子两端，突然要用“>”“<”符号连接式子，学生一下难以适应。这时可让学生体会世上的万物都有正、反两面，对于数学而言，数学中有等式，也有不等式，在学习时难免会有较为“别扭”的感觉，认为不等式就是数学内容中的不和谐因素。实际上不等式也是数学的一种表达式，其以相似确定形式描述了一种无穷及不确定的数学状态。故教师在对这部分内容讲解时，引入概念时要平缓，这样才能自然衔接，纠正学生对不等式的看法。

二、解题中所体现的数学思想

为了更好地帮助学生掌握不等式的有关解题方法，很多教师都绞尽脑汁，总结了很多技巧。例如，“解不等式的方法是利用函数性质，将无理不等式化成有理不等式。高向低次代，转化步步等价……”对于这类技巧，学生如果可以掌握自然是好，但如果无法掌握也不能让学生死记，因此硬背的方式是不可取的。只有真正掌握了不等式推导的起始過程，学生才能牢记于心里。

很多教师在讲解不等式内容时，容易把这一节的内容孤立起来。事实上，不等式就是一个简单函数，需要学生快速联想起函数的定义域、值域等因素，特别要培养学生在遇到根号下整式、分式下分母、底数函数等不等式时，其脑中马上就要想到先求出这些数学因子的定义域，在此范围内再去寻求不等式的解。教师充分考虑各因素并形成科学数学思维，让高中生掌握数学归纳法以及分类讨论法等基本方法不等式就是这样，在未考虑分母、底数函数是否有意义的条件下盲目寻求不等式的解，无法做到等价置换，且容易出错。所以对于易错题的讲解，还是十分必要的。

三、易错题型及解题技巧

1.和线性规划结合问题

此类数学问题在高考数学教学中占据比例是比较大的，并且涉及的数学知识点也比较多，主要是值域、定义域以及面积计算等，在解答此类数学问题时，一定要寻找恰当的解题方法，一旦不等式和线性规划数学性质理解不够具体和详细，那么解题过程将会出现错误。

比如，在学习人教版不等式知识内容时，有这样一

道例题：下有不等式组所表示的平面区域面积

都是等于一的三角形，那么实数k的数值则为（   ）。

A.-1B.—C.—D.1

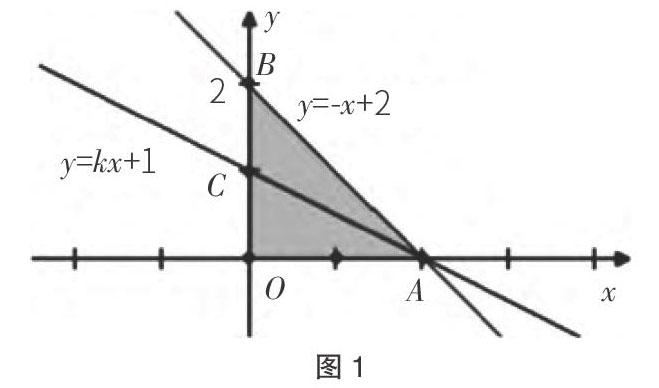
此道数学题所要解决的难点问题，就是三条直线在x、y轴上围成的图形——三角形图形面积的计算，这里也是学生最容易出现问题的地方，解决问题的主要方法就是将三条直线围成的示意图图形面积标出来（如图1所示），然后将A、B、C、D四个答案代入方程式中计算，就可以得到正确答案，通过计算后发现选项B是正确的[1]。

解决此类问题的技巧可以分为两个形式，第一是将问题转化为目标函数最值求解问题，解决问题的关键在于在纸张上绘画出可行域，进而可以更加正确地理解目标函数的几何意义和价值，此思路是正确解决问题的一种方式[2]。

第二则是将目标函数中的参数进行设立设置，主要目的在于提升探索问题的动态性以及问题的开放性，解决问题的关键在于从目标函数结论上入手，针对图形动态关系进行分析，对于整个函数变化过程以及出现的各种相关量进行准确定位，进而可以从此类问题中寻找到解决问题的主要思维方法。

2.高次不等式的解答方法

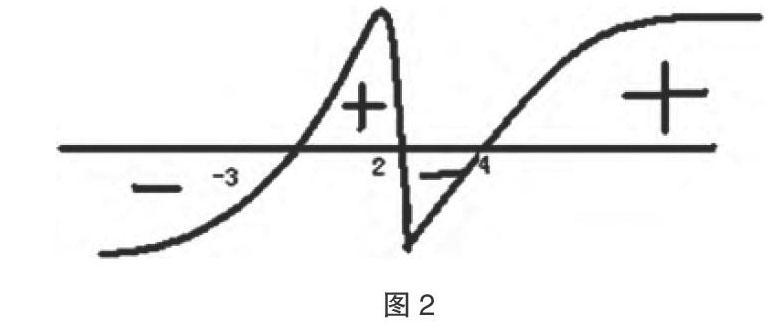
高次不等式易错点主要是学生经常会遗忘数学知识的特殊点，一些特殊区域难免会被学生遗忘，进而无法判断函数升降问题。人教版高中数学不等式章节知识中有一道例题是：求解（x+3）（x-2）（x-4）≤0的解集。此题解答方法和思路是可以在数轴上将方程的三个零点标记出来，分别是-3、2、4，三个零点将整个数轴分为4个区间，如图2所示。

最右边的第一个区间是正数，后边则正负相间，在区间将正负号标记清楚，不等式小于等于0则是符号区间，进而可以得到正确答案。因此此不等式的解集则是{x|2≤x≤4或者x≤-3}。解答此类数学题型的主要技巧在于要善于使用函数图像对区间进行划分，在具体解决问题过程中一定要注意寻找一些特殊点，通过特殊点解决数学问题，加深对知识的理解，从而不断提升学生解决不等式问题的效率。

3.不等式等价转化问题

在学习人教版知识时，一道例题是：不等式|x2-4x+p|+|x-3|≤5的x的最大值是3，那么请求出p的值。学生在解决此类不等式题时容易出现错误的原因是学生并未进行等价转化，无法理解x的最大值是3的真正内涵。

解决问题的主要步骤：因为x的最大值是3，所以x-3<0，原不等式则可以替换为等价的|x2-4x+p|-（x-3）≤5。通过化简可以转化为-x-2≤x2-4x+p≤x+2，最后可以得到{   ，假设①和②的根依次是x1、x2（x2>x1）、x2x3（x4x3），则x2=3或者x4=3，

假如x2=3，那么9-15+p-2=0，所以解得p的数值为8;

假如x4=3，那么9-9+p+2=0，所以解得p的数值为-2;

当p=-2，原不等式组无解，那么p的数值则为8。

学生在解决此类问题时，到了后面则会忘记前面的数学知识，要想真正解决此类问题，就要多做题，多练习，才能够更好地克服和解决学习数学知识带来的负迁移效果。学生不会等价转化方法，就要进行针对性训练，直到学生掌握知识内容为止。不等式是高考数学必考知识点，不等式知识掌握程度直接影响了学生数学成绩，所以在平时做题过程中一定要准备好一本错题集，将容易做错和经常出错的数学题目抄写下来，在题目旁边一定要书写出现错误的原因，经常将错题本拿出来阅读和思考，坚决不能在同一个地方跌倒两次。

4.含参不等式问题

通常解决含参数不等式问题时，需要用到分类讨论方法，选择恰当的分类方式。要想真正解决数学问题，就要分析参数是否为零以及不能重复和遗漏等。比如，人教版例题中关于x的不等式是ax2-2x+1>0，（a是常数，并且a∈R）。遇到此类数学问题，学生就要立即想到采用分类情况进行讨论，分别是a=0、a>0和a<0三种情况，并且在a>0时还要注重有效区别▲的数值。解决此种类型的数学题目一定要记得使用的解题技巧就是参数一定要以分类形式进行讨论，确保整个过程不重复，也不遗漏。基本不等式解决方法就是凑项，拆项，配系数，换元和取倒数的代换。

5.绝对值不等式问题

解决绝对值不等式问题可以通过变形将绝对值符号去除，然后将不等式转化为一元一次以及一元二次不等式组，求解起来更加简单，含有多个绝对值符号的不等式解决方法，一般可以采用零点分段方法进行求解，也可以用解决实数绝对值的方法表示的几何意义进行求解，还要考虑不等式的最值问题。解决问题的主要思路就是通过各种方式将问题转化为不含绝对值符号的一个简单式子进行计算。

6.不等式恒成立问题

不等式恒成立问题一般会和高中数学知识中数列以及抽象函数结合起来，此类数学问题属于高中数学不等式问题的难点问题，对于学生来说都是比较抽象的，容易出现错误，比如，人教版不等式例题函数f（x）-Ln（1+x）， g（x）=xf'（x），x≥0，其中f'（x）是f（x）的导函数。

（1）假设g1（x）=g（x），gn+1（x）=g（gn（x）），n∈N+，求出gn（x）的表达式。

（2）假设f（x）≥ag（x）恒成立，那么请求出a的取值范围。

（3）假设n∈N+，对比g（1）+g（2）+...+g（n）和n- f（n）的大小，并通過简单解题步骤进行证明。

此道数学例题考查的是不等式和函数导数闭区间的最值问题，依照函数单调性问题，解决此类数学问题一般要使用分离变量以及变形方案，或者使用变换主元以及构造函数的方法进行解决，还可以使用函数单调性和基本不等式形式求解，最值问题可以通过一种方式转化为基本不等式进行求解，并且在转化不等式过程中还要格外注意不等式等号方向，解决问题期间要注意一正二定三相等。

综上所述，在解决高中数学问题时一定要高度重视数学实践内容，对不等式知识内容容易出错题型进行整理和记录，做好不等式证明、转化和最值求解工作，掌握具体解题技巧，从而可以更好地解决数学问题，以便于在高考中获得更好的成绩。

[参考文献]

[1]吴建芬.高中数学不等式易错题分析[J].中学数学，2018（13）.

[2]王 楠.高中数学不等式易错题型及解题技巧[J].好家长，2017（40）.

课题项目：高中数学“先学后教”与“先教后学”教学模式的比较研究（20164617）。

作者简介：李 静（1990— ），女，吉林长春人，中学一级教师，本科，研究方向：高中数学教学。