焦石坝地区页岩Cole-Cole模型参数的快速计算方法
2020-09-25刘智颖张柏桥李铭华
刘智颖,张柏桥,许 巍,罗 兵,李铭华,黎 伟
(1.中国石化江汉油田分公司勘探开发研究院,湖北武汉430223;2.长江大学地球物理与石油资源学院,湖北武汉430100)
Cole-Cole 模型是由PELTON 等人于1932年提出的泥页岩孔隙电流传导模型[1-2],主要用于描述泥页岩复电阻率随交流电源频率变化。标准的Cole-Cole 模型包含4 个参数,即ρ0、m、τ和c。这些参数可以反映页岩的孔隙结构、矿物组分等特征[3-4]。如何利用岩心复电阻率频谱实验数据快速、准确地求出这4个参数,是重要的研究课题。
通常,最小二乘法程序的寻优算法有模拟退火、遗传算法及梯度下降算法等。虽然模拟退火、遗传算法等全局寻优算法可以有效避免陷入局部极小值的问题[5-7],但其运算速度难以保证。相比之下,采用梯度下降算法更能保证运算速度和收敛性[8-9]。然而,过多的参数不仅造成巨大的运算量,而且增加了迭代算法陷入局部极小值的可能性。为了降低Cole-Cole 模型的复杂程度,PELTON 和MADDEN等[1,10]根据常见储层的极化作用的类型及其特点,对标准Cole-Cole模型进行了简化,将参数c给定为1/4、1/2 等值。这样,最小二乘法的寻优参数只剩下ρ0、m和τ这3个值,提高了运算速度。大量的实践表明,前人提出的Cole-Cole 简化模型在许多地区的应用效果良好。然而,实际岩心复电阻率资料表明,焦石坝地区c值的变化范围较大,不能将参数c设为恒定值。同时,该地区参数τ的数量级相较ρ0、m和c很小,造成最小二乘法中的梯度下降算法难以保证一致收敛性,严重降低了收敛速度,甚至导致无法收敛。也就是说,此时梯度下降算法是病态的[11]。具体表现在:寻优过程中,τ的迭代值会出现负值,超出其定义域,导致程序计算错误而无法收敛。如果简单地将搜索步长s减小,虽然可以解决该问题,但程序计算速度严重减慢。
针对上述问题,通过从极值和渐近性质两个方面对标准Cole-Cole 模型函数进行深入分析,给出了参数τ的一种简便计算方法,以及ρ0、m和c这3 个参数的迭代初始值预估算法。不仅使得最小二乘法寻优参数由原来的4个减少为3个,而且给出了ρ0、m和c的初始值,从而有效改善了程序收敛性。同时,还对梯度下降法的迭代步长进行了改进,给出了最优步长。通过以上两项优化,程序的运算性能明显提高。以焦石坝地区某井的岩心复电阻率频谱数据为例,对改进前和改进后的程序运算速度进行了对比。对比结果表明,在相同的计算精度要求下,改进后的计算程序的迭代次数下降幅度较大,计算速度显著提高。
1 参数的迭代初始值预估算法
选取合适的迭代初始值,对于改善程序的收敛性有很大的帮助。本文给出了ρ0、m、τ和c这4 个参数的初始值预算法,其中参数τ的初始值即为其寻优结果,因而以上4个寻优参数简化为3个。
1.1 标准Cole-Cole模型简介
标准Cole-Cole 模型函数描述了岩心复电阻率的实部和虚部随电源频率的变化情况[12]。形式如下:

式中:ρ为岩心复电阻率,Ω·m;ρ0为直流电阻率,Ω·m;m为极化率;i为虚数单位;ω为交流电源的角频率,rad/s;τ为极化弛豫特征时间,s/rad;c是一个与极化类型有关的数[1]。
1.2 模型函数的极值及渐近性质
为了给出待求参数τ、ρ0、m、c初始值的预估方法,从极值和渐近性质两个方面对式(1)进行了分析。
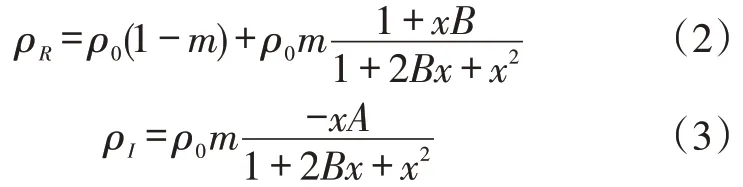
式中:ρR和ρI分别是岩心复电阻率ρ的实部和虚部。
现有研究表明,ρI(ω)曲线有一个极小值点[2],首先对此极小值点的位置进行了分析,可以看出,用驻点法求式(3)极小值将导致求导运算烦琐,为此,应用不等式法求出了ρI(ω)的极值及极值点的位置。

对于c∈(0,1)[1],可以看出A和B均大于0。因此,应用重要不等式得:

当且仅当:x=1时取等号。
将式(5)代入式(4),并应用复合函数增减性原理可得:

当且仅当:x=1时取等号。
考虑到∀c∈(0,1)有x是ω的单调增函数,则当ωτ=1 时ρI取极小值。即当时,式(1)的虚部ρI有且仅有一个极小值点。


显然h(x)是单调递增函数。应用复合函数增减性原理可得,ρR是x(或ω)的单调递减函数,没有极值点。此外,对于x=0的值和x→∞的渐近性质有:

当x→∞时,根据洛毕达法则不难得出:

最后,对式(2)和式(3)在x=0处的导数进行了计算。得出:
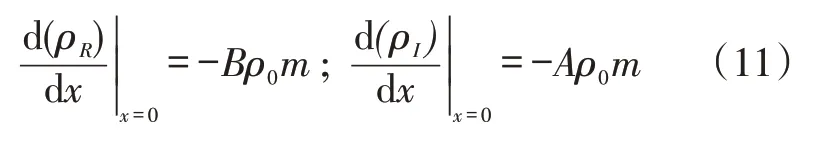
1.3 初值预估方法
根据前面的分析,结合本文使用的测量岩心复电阻率的阻抗分析仪TH2839A 的工作频率,提出了τ、ρ0、m、c这4 个参数的初始值预估方法。文中将ρ0、m、c的初始值记作、m(0)、c(0)。
TH2839A 的工作频率范围是20 Hz ~4 MHz,可以输出101个频率下的岩心复电阻率数据。
1.3.1 参数τ的计算
先利用岩心复电阻率频谱实验数据绘制实部和虚部的频谱曲线,找出虚部曲线的极小值对应的交流电角频率值(记作:ω0),然后取ω0的倒数即可确定τ的初始值。根据式(6),此方法可以求出τ的严格解,因此,将这样求得的初始值直接视为τ的寻优结果。
求ω0的具体方法是:先在仪器输出的101 个岩心复电阻率的虚部值中找出最小值,然后提取与该最小值相邻的两个工作频率的复电阻率虚部值,再将这3 个虚部值及其各自对应的3 个工作频率拟合为二次函数,最后利用二次函数的极值公式求出其极小值点对应的角频率(图1)。图1中蓝色点是测量的复电阻率虚部的最小值,该值不一定是严格的虚部最小值;绿色点是与之相邻的2个数据点。虚线是二次拟合函数,其极小值对应的角频率即为ω0。
实际算例表明,可以将该方法求出的τ值作为τ的寻优结果。精度完全满足要求,无需将τ代入最小二乘法寻优程序中。

图1 ω0 计算方法Fig.1 Computing method of ω0
1.3.2ρ0和m的迭代初始值
根据式(9)可以看出,可以选取20 Hz 时的复电阻率的实部值作为。算法为:


1.3.3c的迭代初始值
由式(11)可以看出,由于A和B都是c的函数,因此,只要知道和,即可确定c的值。和可以根据最小的2 个工作频率(20 Hz和22.6 Hz)下测量的复电阻率值,应用差分法求出。这样,式(11)即为一个关于c的方程组,方程组的解即可作为c的迭代初始值c(0)。

将式(14)和式(15)联立为一个关于c的非线性超定方程组可以证明,在c∈(0,1)区间中,该方程组必存在一个最优解。
由于无须严格求解c的值,因而采用枚举法,从0.1,0.2,…,0.9 这9 个值中进行试探。这样,仅需9次计算,即可找出最符合式(14)和式(15)的c值,作为迭代初始值c(0)。
2 用最小二乘法求ρ0、m和c
最小二乘法程序通过搜索误差函数的最小值来确定待求参数的值。构造了如下误差函数(式16),该式为不同电源频率下式(1)算出的岩心电阻率的实部和虚部(ρRi、ρIi)与实际测量的岩心电阻率的实部和虚部(ηi、μi)之差的平方和。
然而,尽管寻优的目标函数是式(16),但其不适合用于描述迭代的精度。这是由于对于完全相同的计算精度,如果N越大,则式(16)的值越大,这样不利于检验算法的计算精度。因此,用相对误差式(17)作为判断迭代精度的标准。
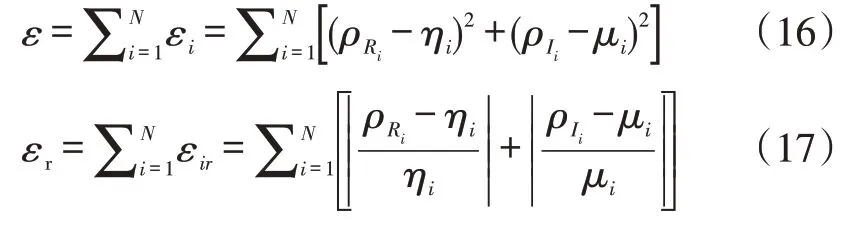
式中:ρRi和ρIi分别表示式(1)计算出的第i个电源频率下岩心复电阻率的实部和虚部,ηi和μi分别表示实际测量的第i个电源频率下岩心复电阻率的实部和虚部,N为实验仪器的频率的个数。
2.1 改进前的梯度下降法
假设程序已经搜索至第k步,当前的参数值分别为ρ0(k)、m(k)、c(k)和τ(k)。此时,式(16)的值及其梯度分别为:

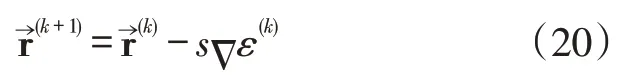
此时,式(19)的值为:
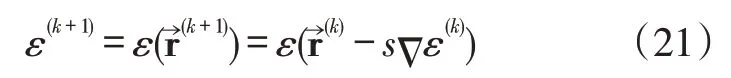
一般给定一个较小的搜索步长s(本文取7.0×10-5),即可使得迭代序列{:k=0,1,2,.....}收敛到4个待求参数ρ0、m、c和τ的精确结果。
2.2 对迭代步长的改进
为提高程序运算速度,直接用1.3.1 节中的方法求出τ,并对迭代步长s进行了改进。
仍然假设程序已经搜索至第k步,在的邻域内将式(21)展开为泰勒级数,可用于表示的近似值。
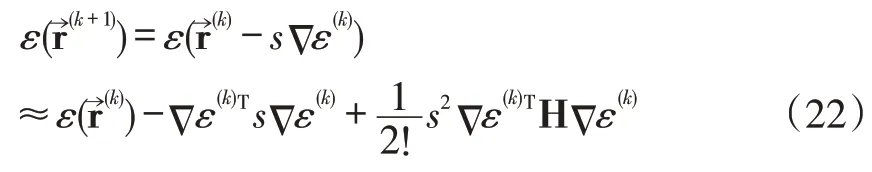
其中:
精细化学品课程体系、课程内容的设置对化工专业学生专业能力和创新创业能力的培养起着至关重要的作用.随着时代的进步,在全民创业、万众创新的时代背景下,高校的人才培养应该致力于满足社会需求,培养学生的创新创业能力.精细化学品课程教学应该立足于专业的客观实际,依据当前的发展现状合理地安排、调整教学内容,及时了解精细化学品领域最新的发展动态、前沿领域,与时俱进,选择合适的教学手段和方法,不断更新、完善课程教学.精细化学品课程教学改革任重而道远,作为高校教师,应该了解当下的实际情况,立足于创新、创业、应用型化工人才培养目标,积极探索精细化学品课程教学的新理念、新方法.

式中:x的定义与式(2)或式(3)相同。
由式(22)可以看出,第k+1 步的误差函数值ε(r→(k+1))可以用一个关于搜索步长s的二次函数近似表示。这表明,只要s取值范围足够小,使得式(22)与ε(r→(k+1))的差别不大,式(22)将存在极小值。也就是说,选择最优的迭代步长,可使得误差函数式(18)下降幅度达到最大。该最优迭代步长(记作s0)可由式(22)的一阶导数确定[15]。
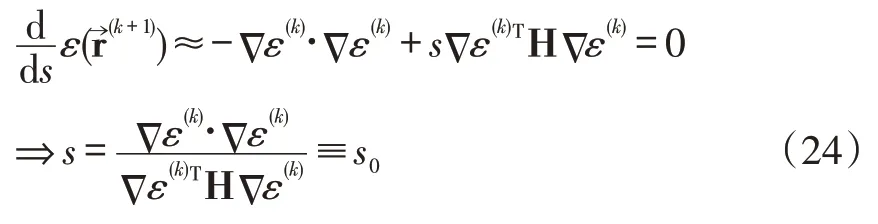
显然,如果矩阵H 是正定矩阵,则s0必然给出式(22)的极小值[16],满足最优搜索步长的条件。
然而,如果直接将s0设定为搜索步长,可能存在两个问题:①如果H 是非正定的,s0就有可能小于0,而完全根据数学定义检验H的正定性又是十分烦琐的;②当s0过大时,式(22)的值将不再近似等于,造成s0不再是最优的搜索步长。本文采用了一种较为简单的确定搜索步长的方法。
事实上,通过观察式(22)不难发现,即使H不是正定矩阵,只要s取得足够小,序列{r→(k):k=0,1,2,.....}仍然是收敛的。
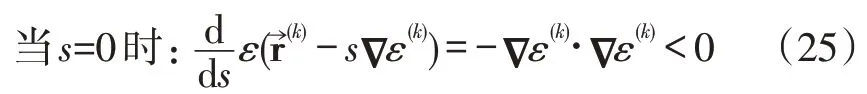
式(25)表明,只要s足够小,就有ε(r→(k+1))<ε(r→(k))。说明即使用式(24)求出的s0<0,不能作为迭代步长,但此时只要给一个较小的搜索步长s即可,本文选择1×10-7。
综上所述,以1×10-7作为判断s0大小的标准,若s0>1×10-7或s0<0则取s=1×10-7,若0<s0<1×10-7则取s=s0。
3 计算实例
将改进前的算法和改进后的算法用于焦石坝地区某井的岩心复电阻率频谱数据处理,计算出了ρ0、m、τ、c4 个参数。下面以焦石坝页岩气田某区块的8XX 井中2 号样、18 号样、23 号样为例,说明不同算法的计算效果。岩心钻切档案资料见表1,实验测量的复电阻率频谱数据见图2中的数据点。
编制了3个最小二乘法计算程序:第1个程序是将迭代步长设为定值(1×10-7),并随机给定迭代初始值;第2个程序采用了2.2小节描述的最优步长算法,但迭代初始值同第1个程序;第3个程序同时采用了文中的迭代初始值预估方法和最优步长算法。3 个程序迭代计算过程中的相关参数见表2—表7。用第3 个程序求出的4 个参数绘制的复电阻率频谱曲线见图2中的实线。

表1 8XX井部分岩心钻切档案资料Table1 Records of several rock cores of well-8XX
可以看出,在相同的相对误差条件下,虽然程序2(表4、表5)比程序1(表2、表3)在总迭代次数方面虽然有一定进步,但算法收敛性仍然不佳,无法满足实际生产的要求。算法3(表6、表7)不仅收敛性很好,而且迭代次数大幅减少,程序运算速度显著提高。

表2 程序1的参数及计算结果Table2 Parameters and computing results of program-1
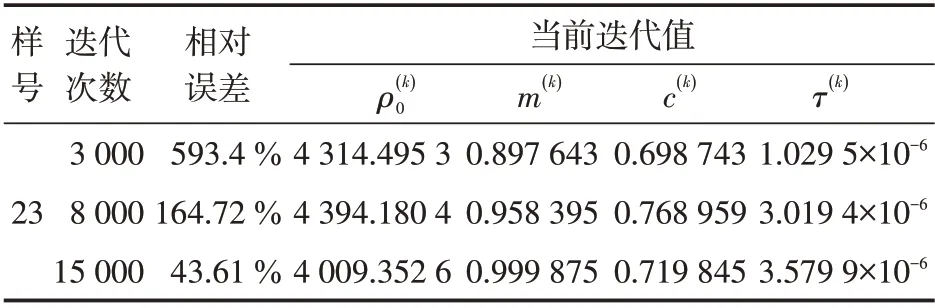
表3 程序1的运行过程Table3 Processing of program-1

表4 程序2的参数及计算结果Table4 Parameters and computing results of program-2

图2 岩心复电阻率频谱数据(数据点)与用程序求出的参数绘制的频谱曲线(实线)对比Fig.2 Comparison between real measured complex resistivity data and the calculations from program
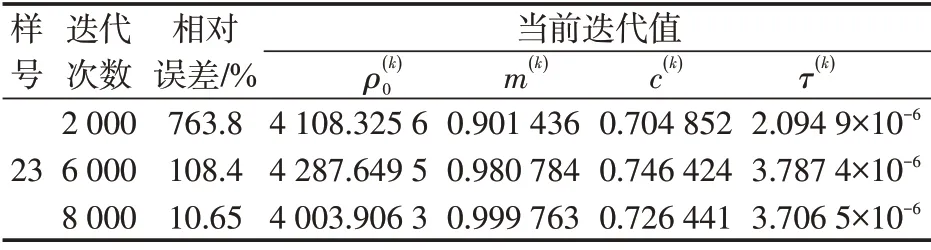
表5 程序2的运行过程Table5 Processing of program-2
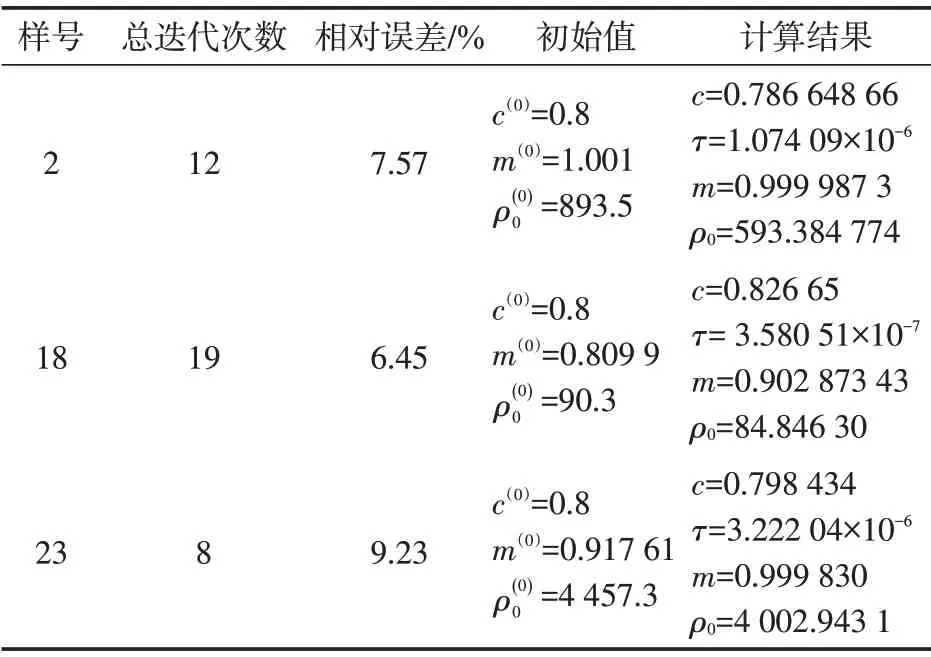
表6 程序3的参数及计算结果Table6 Parameters and computing results of program-3

表7 程序3的运行过程Table7 Processing of program-3
4 结论与讨论
1)焦石坝地区页岩储层的参数c变化范围较大,因而不能采用前人设计的简化的Cole-Cole 模型,而必须使用标准Cole-Cole模型。同时,参数τ值过小,严重影响了最小二乘法寻优程序的收敛性。
2)通过分析标准Cole-Cole 模型函数的极值点和渐近特性,发现参数τ值可以直接利用虚部曲线的极小值位置求出。同时,给出了ρ0、m和c这3个参数较好的迭代初始值计算方法,显著改善了最小二乘法程序的收敛性。
3)对于复杂的非线性寻优问题,如果将搜索步长设为固定值可能造成收敛速度过慢,而在迭代点的邻域内,对寻优目标函数进行泰勒级数展开,可获得最优的搜索步长,使得算法收敛速度加快。
4)本文并未考虑算法的鲁棒性。事实上,由于TH2839A 阻抗分析仪的相敏部件的测量误差,以及焦石坝地区的一些复杂的矿物,使得在某些频率段岩心复电阻率与标准Cole-Cole 模型有较大差异。这些异常数据对算法鲁棒性提出了一定要求,下一步工作将围绕此问题展开。
