卡方分布的Excel构建与模拟

查岭生，李 俊，丁建华

（淮北师范大学 生命科学学院，安徽 淮北 235000）

0 引言

卡方分布（Chi-square distribution，χ2）是一种常见的概率分布，在生物统计学的教学中占有重要位置. 它的定义为：假设从标准正态总体中随机抽取k个独立变量，就会得到u1,u2,…,uk，把这k个随机变量先平方、再求和，这个和被定义为χ2，即

每进行一次随机抽样便可获得一个χ2值，于是，所有可能的χ2值所构成的分布被称作χ2分布［1］. 该分布属于连续型变量的分布，自由度df=k-1，每个不同的自由度都有一个相应的分布曲线［1-2］.χ2分布具有以下特征：其取值区间为［0，+∞）；当df=1时，分布曲线以纵轴为渐近线；当df逐渐增大时，分布曲线渐趋于左右对称；当df≥30时，χ2分布已接近于正态分布［1］.

在具体的教学活动中，如果对χ2分布曲线的特征仅仅是进行简单的叙述，一方面难以引起学生的学习兴趣、激发他们的学习热情，另一方面也不利于他们对χ2分布内涵的深入理解. 作为一种非常普及的办公软件，Excel具有强大的函数运算能力，在统计学教学过程中得到广泛应用［3-6］. 人们利用Excel对抽样分布［7］、中心极限定理［8］、大数定律［9］等内容进行模拟，以帮助学生对这些概念的深入理解. 近年来，笔者与同事们在教学过程中，利用Excel对生物统计学当中的一些内容进行构建或模拟，也取得不错的教学效果［10-14］. 本文继续以Excel 2010为例，采用2种方法对χ2分布曲线分别进行构建和模拟，以供参考.

1 利用函数进行构建

Excel 2010中的CHISQ.DIST（χ2，df，FALSE）函数可以用来计算某χ2值与df条件下的概率密度. 利用该函数对χ2分布曲线进行构建时，其数据输入格式如图1所示. 在A列中自A3单元格以下输入≥0的数字以表示χ2值，本文中以0.5为间隔，即0.0、0.5、1.0、…；在第2行中自B列开始输入正整数以表示自由度，本文中以1、3、5、…为例；在B3单元格中输入“=CHISQ.DIST（$A3，B$2，FALSE）”，并将此函数公式向右、向下复制填充，一张特定χ2值与df条件下的概率密度表格便生成了；然后对所得概率密度与A列当中的χ2值进行绘图，便可得到相应的χ2分布曲线（图2）. 该文件生成后，只需要任意修改表格第2行中的自由度取值，便可以在课堂上动态地展示χ2分布曲线随df变化而变化的规律特点，从而达到激发学生学习兴趣、提高教学效果之目的. 需要注意的是，当χ2=0、df=1时，Excel将返回错误值“#NUM！”，这是因为此时曲线以纵轴为渐近线的缘故.

图1 Excel函数输入示例

图2 不同自由度的χ2 分布曲线

2 利用VBA编程进行模拟

2.1 模拟步骤

Excel中的NormInv（Rnd（），0，1）函数可以生成一系列服从标准正态分布N（0，1）的随机数字，正好可以用来模拟χ2分布的抽样过程.

第1步：打开Excel 2010，新建一个电子表格，在当前工作表Sheet1的A1至A3单元格中分别输入“自由度df=”“抽样次数=”“组距=”；在B1至B3单元格中分别输入相应的数字，本文中以自由度df=1、抽样次数=10 000、组距=0.5为例；在C1至G1单元格汇总分别输入“u”“u2”“χ2”“组限”以及“频率”（图3）.

第2步：按Alt+F11进入Visual Basic 编写界面，双击左侧的Sheet1图标，进入代码编写界面，把本文附录中的VBA代码拷贝进去（图4）. 然后关闭代码编写界面进入工作表界面，将文件另存为启用宏的文件类型（*. xlsm）即可.

2.2 模拟结果

在B1 单元格中输入具体的数字（本文中以df= 1 为例），便可触发该模拟程序自动运行. 首先是在C2、C3 单元格中生成2 个服从N（0，1）的随机变量，此步骤用来模拟从标准正态总体当中随机抽取k（=df+1）个独立变量的过程；然后对这2个随机变量求平方，其平方值相应地存放在D2、D3单元格中；再对D2、D3单元格中的平方值进行求和，得到一个χ2值，将其存放在E2单元格中. 若将上述抽样过程重复10 000 次（B2 单元格中的数字），便可以得到 10 000 个χ2值，依次被存放在 E2 至 E10001 单元格中（图3）.

图3 模拟步骤第1步的输入结果

图4 Excel中VBA代码的输入

在VBA 代码中，采用ROUNDUP（MAX（））和ROUNDDOWN（MIN（））这两个复合函数对E 列中的χ2值的最大值与最小值分别向上向下取整数，以统计χ2值的分布范围，并根据B3单元格中的组距大小设置组限，数据存放在F列中；再采用FREQUENCY 函数进行频次统计，所得的各组的频率存放在G列中；最后对G列中的结果绘制柱状图. 绘图时可采用动态引用函数OFFSET以达到动态展示的效果，其具体步骤如下：

图5 定义名称对话框

图6 选择数据源对话框

通过上述操作，一幅可以随F列、G列中数据变化而变化的动态柱状图便生成了，稍加修饰，其效果如图7所示. 任意修改B1单元格中的自由度取值，该柱状图便会相应地发生改变，从而可以动态地展示χ2分布随自由度变化而变化的基本规律. 从图7中可以看出，χ2值的频率分布变化趋势与图2中的概率密度曲线的变化趋势是基本一致的.

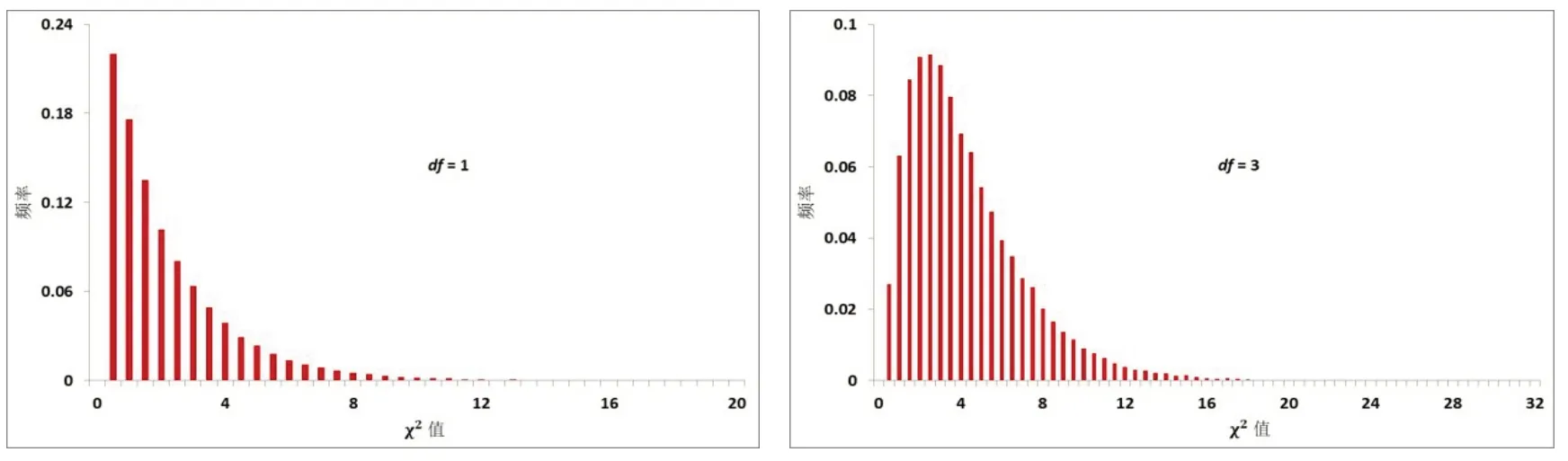
图7 不同自由度的χ2 频率分布

3 讨论

频率与概率之间的关系，实际上就是样本统计数与总体参数的关系. 根据大数定律，当样本容量n充分大时，事件A 发生的频率W（A）就可以代替概率P（A）［1］. 上述的第1种方法，即利用CHISQ.DIST函数对χ2分布曲线进行构建，恰恰就是对χ2分布总体的描述. 其优点是分布曲线圆滑美观，运算速度快，不影响正常的教学节奏，便于课堂上展示；其不足之处在于未能体现抽样过程，也就不便于学生深刻理解χ2分布的由来. 利用VBA编程对χ2分布进行模拟则可以很好地弥补这一不足之处. 在VBA模拟中，学生可以根据运算过程去梳理χ2分布的由来，从而加深对该分布的理解. 理论上，当图3中B2单元格中的抽样次数无限大、B3单元格中的组距无限接近于0时，图7与图2相一致. 在实际应用时，一方面Excel无法满足抽样次数无限大的要求，另一方面，抽样次数过大也会使得运算过程耗时过长. 本文的VBA代码中，最大抽样次数设置为65 535，已然可以基本满足模拟的需要. 建议：在课堂上采用第1种方法辅助教学，将第2种方法留给学生课下自行模拟，通过修改B1至B3单元格中的模拟参数，以查看不同自由度、不同抽样次数以及不同组距下的χ2频率分布. 这种课上课下相结合的教学方式，必能激发学生的学习兴趣，提高教学效果.

致谢：特别感谢福建江夏学院会计学院的薛捷波先生在VBA编程方面给予的热情帮助.