一个分式型Weitzenbock不等式的九层隔离①

钟建新

(江西省赣州师范高等专科学校 341000)

近年来，对Weitzenbock，Finsler-Hadwiger不等式的研究精彩纷呈，文[2]总结了一系列研究成果，其中有：

设a,b,c,S,r,R分别是△ABC的边长、面积、内切圆半径与外接圆半径，则

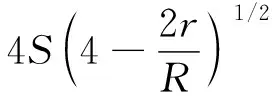
设a,b,c,S,p分别是△ABC的边长、面积和半周长，则

文[3]给出一个加强不等式：设a,b,c,S,r,R分别是△ABC的边长、面积、内切圆半径与外接圆半径，则

文[4]刊出一个拓展不等式：设a,b,c,S,p分别是△ABC的边长、面积、半周长，pa=p-a，pb=p-b,pc=p-c，则

文[5]进一步给出如下加强不等式：

≤∑a2-∑(a-b)2

定理设a,b,c,S,r,R,p分别是△ABC的边长、面积、内切圆半径、外接圆半径与半周长，则

(∑表循环和，∏表循环积)

证明对不等式链逐层证明如下.

据平凡不等式3∑a2≥(∑a)2，

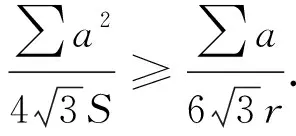
由均值不等式

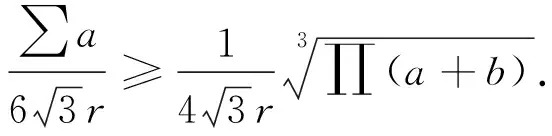
因(a+b)(b+c)(c+a)=(∑a)(∑ab)-abc，

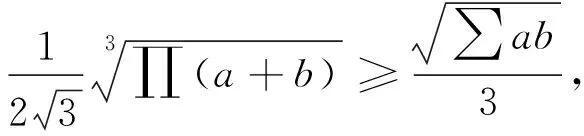
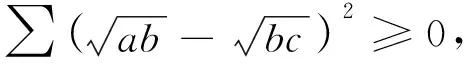
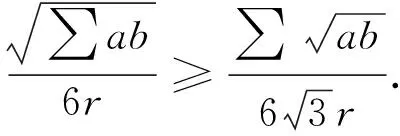
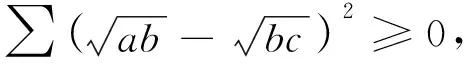
由均值不等式得

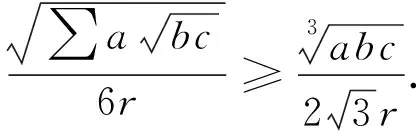
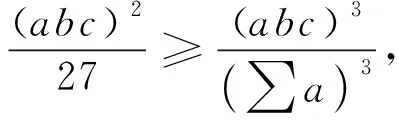
由均值不等式得

b2c2+c2a2≥2abc2,c2a2+a2b2≥2bca2,

a2b2+b2c2≥2cab2,

相加得∑a2b2≥abc(∑a),

从而有(∑ab)2≥3abc(∑a),

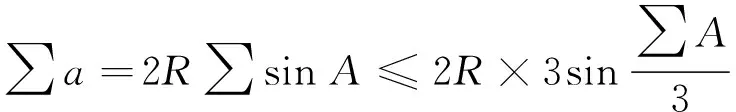
以上证明过程顺次相连便得分式型Weitzenbock不等式的九层隔离：

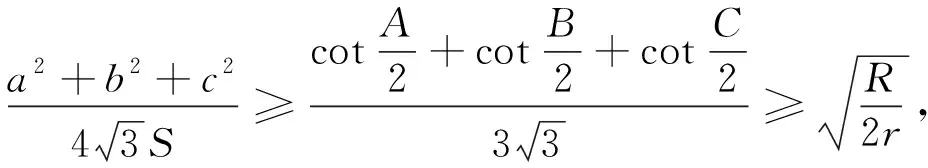
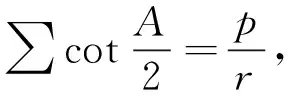
据平凡不等式 3∑a2≥(∑a)2，