也谈“好的例题教学是照亮学生解题的灯塔”

郑 瑄 沈吉儿

(1.浙江省宁波市江北区教育局教研室 315000 2.浙江省宁波教育学院 315000)

《数学通报》2017年第4期，臧华老师撰文“好的例题教学是照亮学生解题的灯塔”，同年《数学通报》第10期，陈延付老师继续撰文“再谈好的例题教学是照亮学生解题的灯塔”.笔者也深深地被此标题所吸引.悉心拜读，怦然心动，共振共鸣，启迪良多.二位老师，从高中数学教学的层面，阐述、分享了解题教学的心得，引发笔者从初中数学教学的层面，对解题教学的实践进行了回顾、省思和整理，如今也撰文如下，就教同仁.

1 思考

首先，有三点值得思考：何为好的例题？何为好的解题？何为好的解题教学？此处，彰显着教师对数学本质的理解与通透，对数学问题的品析与鉴赏，对数学教学持有的基于人性关怀与人文情怀的独特的教学观.

何为好的例题？选择的标准是什么？仁者见仁、智者见智.况且，一千个观者眼里有一千个哈姆雷特.笔者以为，例题的选择，既要考虑对知识的形成、巩固、拓展有裨益；又要关注问题的典型性、方法的启迪性、思维方式的科学性、思维品质的培植性；还要有趣味、有品味、有意味；更要能够体现数学独特的育人价值，此乃数学的独特贡献之所在.

好的解题，是循自然而动，由着蔓藤(条件和规则)，攀援(思考和探究)向前，优雅、流畅且意蕴绵长，过程中无不领略着遇见灵感和顿悟感佩的美好，同时，又不乏智慧与挑战.臃肿、笨拙、突兀的解题方法，总不能令人愉悦和欣然，只能引起沮丧和泄气.此时，还要特别关注的是，当诸多解题方法纷至沓来之时，定要梳理、反思、归纳其背后的共性与共融.

何为好的解题教学？答案自然是缤纷多彩、众说纭纭.然而，最令笔者惊叹和触动的是波利亚《怎样解题》开篇第一部分“在教室里”的一段话：

学生应当获得尽可能多的独立工作的经验.但是，如果把问题留给他一人而不给他任何帮助，或者帮助不足，那么他可能根本得不到提高.而如果教师的帮助太多，就没有什么工作留给学生了.教师应当帮助学生，但不能太多，也不能太少，这样才能使学生有一个合理的工作量.如果学生不太能够独立工作，那么教师也至少应当使他感觉自己是在独立工作.为了做到这一点，教师应当谨慎地、不露痕迹地帮助学生.然而，最好是顺乎自然地帮助学生.教师应当把自己放在学生的位置上，他应当看到学生的情况，应当努力去理解学生心里正在想什么，然后提出一个问题或是指出一个步骤，而这正是学生自己原本应想到的.

波利亚此言易懂，但是真正践行其实很难.因为直接传授结果与告知答案，远比“谨慎地、不露痕迹地帮助学生”要容易的多.更深层次地思考，教师培植学生拥有的不仅仅是“独立工作”的能力，更是培植学生由此而拥有的独立的人格.就似陈寅恪先生的信仰，亦是他一生的追求——独立之精神，自由之思想.达至做人、做事、做学问的和谐统一.

再者，数学学习和研究，数学教育和教学，没有解题万万不能，但仅有解题远远不够.

作为教师的我们，题目如何教得完？作为学生的孩子们，题目如何解得完？

关键是在解题教学中，教师带领着学生在解题中学会解题.在解题中学会思考(怎么想)，在解题中学会行动(怎么做)，在解题中学会反思(怎么悟).这与波利亚《怎样解题》中的四个步骤(理解题目、拟定方案、执行方案、回顾)一脉相承！尤其是貌似无用之用的“回顾”，正是和王国维先生的“出乎其外、故有高致”遥相致意.

当然，更重要的是，在数学问题的解决过程中，领略品赏数学之美，培植理性精神与核心素养，达至精神世界的愉悦和生命状态的超然.

2 三个案例

2.1 苏格拉底的谬误问题

《数学通报》2016年第8期与2017年第10期，代钦教授的文章都提到了“苏格拉底的谬误问题”.笔者将其作为例题呈现于七年级的学生们，并一起展开了探究，非常有趣.

自线段AB的两端作等长的线段AD和BC，使∠ABC为直角，∠BAD为钝角.连结CD并作线段AB、CD的中垂线OM、ON，相交于O点. 则AO=BO，CO=DO. 又AD=BC. 得△AOD≌△BOC，得∠OAD=∠OBC，又∠OAB=∠OBA，故∠BAD=∠ABC，即钝角等于直角(图1).

图1

正如代钦教授的描述，48名学生的班级，最初几乎人人都表现出十分的错愕和惊讶.

很快的，众生云：不可能，这绝对不可能！

教师问：那么，问题可能出在哪儿呢？

学生们议论纷纷，继而开始动手尝试，不过情态各异：一部分学生按老师提供的图形，如素描般的在课堂练习本上依样画葫芦地画出图形，并开始分析；11名学生用三角板、直尺画出草图进行思考；6名学生利用一副三角板、圆规等作图工具依据题意进行作图和考量(中垂线有用尺规作图的，也有用刻度尺和直角作图的)；当然，还有个别只是瞪大两眼盯着黑板上的图形琢磨着……

过不了多久，就有学生果断地发表观点：交点O可能不在上方！

马上有学生继续表达：交点O不可能在线段AB上.确实如此，全等三角形对应角相等.

现在，似乎有一丝丝光明在前方闪耀.

好，若交点O在线段AB的下方，教师出示给学生们看(图2)：

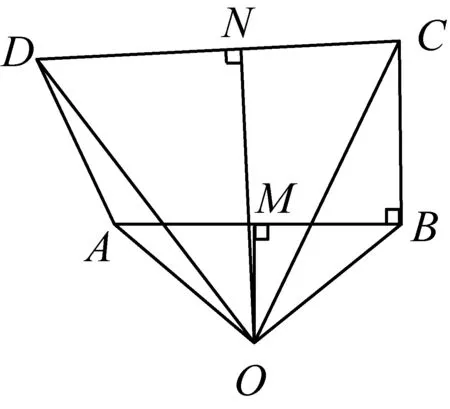
图2

同理可证得∠OAD=∠OBC，两边分别减去∠OAB及∠OBA，结果还是∠BAD=∠ABC.

总之，钝角等于直角.

刚刚见到的一丝光明，瞬间熄灭.why？众生又陷入困境.

图8的方案链长与平均得分显示出大致的线性关系，表明持续的修改会使方案质量得到提高，但修改行为不一定是在同一个设计师手里完成的。

终于，有一位学生迟迟疑疑地说：交点O可能在下方更远一些的地方(有一回一位同仁揣摩可能在上方更远一些的地方).难道远、近有讲究吗？

教师请适才依据题意准确作图的学生呈现他们的成果(图3)，发现OD与AD的位置关系是根本所在，图2中OD在AD的右侧，图3中OD在AD的左侧. 原因找到了，一切恍然.

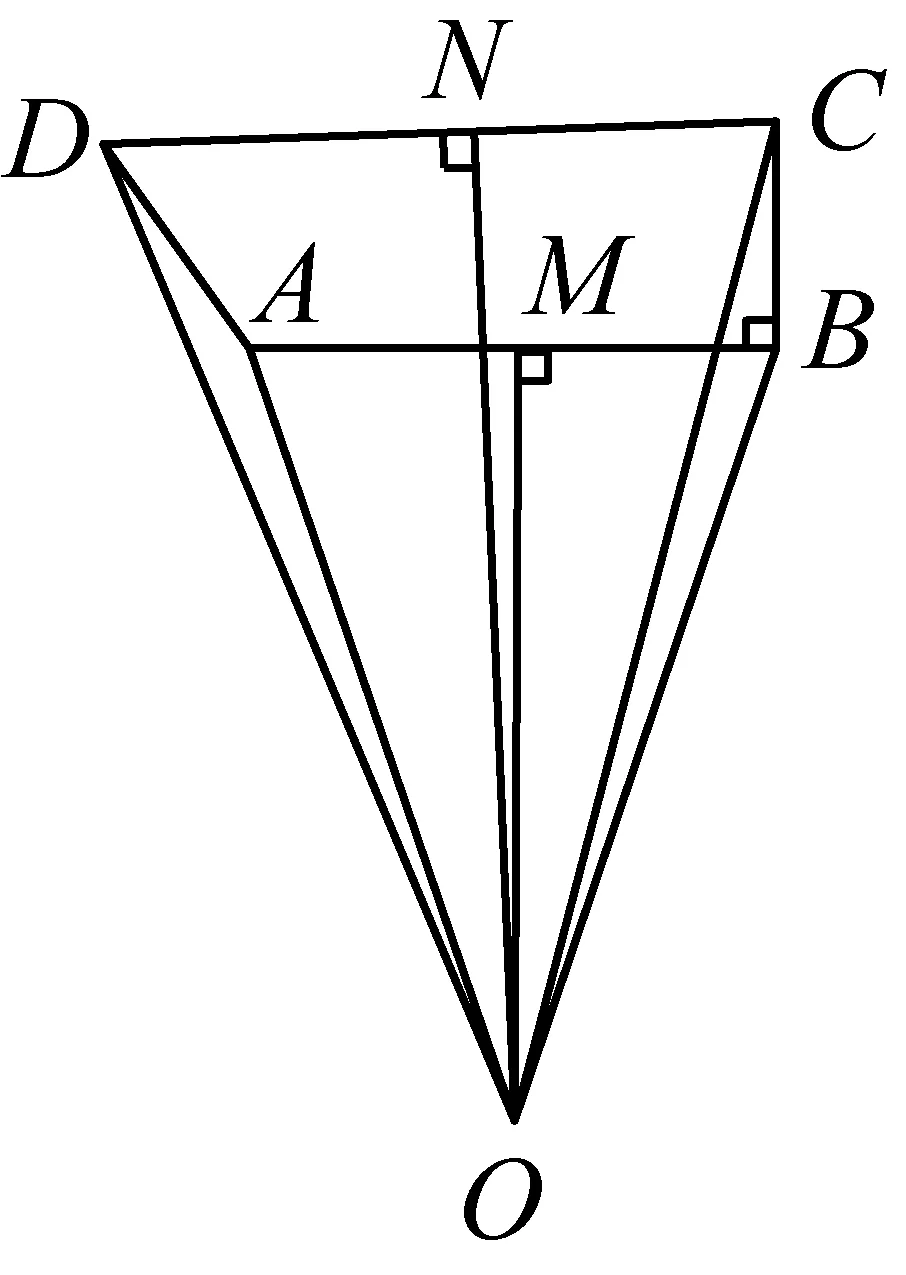
图3

有一些思考和感悟，师生们共同归纳与分享.

在数学学习和理性思考中，不能以直观的表象为依据，而应该以严格的逻辑为根据.

(1)数学层面：论“准确严谨作图”的重要性.

(2)素养层面：论培植“思辨检审、理性解释”能力的重要性(批判性思维、创造性思维).

(3)人生层面：论养成“专注坚持、自律自省、求真求是”品行德性的重要性.

此乃数学教育之“立德树人”之贡献所在.

2.2 阿波罗尼斯圆

阿波罗尼斯，古希腊数学家，与欧几里得、阿基米德齐名.阿波罗尼斯圆是他论著中的一个著名问题：已知平面上两点A、B，则所有满足PA/PB=k，k>0且k≠1的点P的轨迹是一个圆，也称阿氏圆.历年中、高考试题中都会依稀仿佛见到其踪影.笔者也将其作为例题呈现于九年级的学生们，并与学生们一起进行了探究，教学过程回味无穷.

笔者首先给出的是这样一个问题(图4)：

图4

图5

已知：△ABC中，AB=3，AC=2BC，

求: △ABC面积的最大值.

师问：你们是怎么想的呢？

生答：特殊位置！曾经的经验，邻边已知的平行四边形，当邻边互相垂直时，面积最大.

哦，联想到记忆中的经历和经验——模型和范式.

解二：代数的自然联想.根据三角形的面积公式，学生们希望能够寻求AB边上高线的最大值，这确实是自然而然的思维走向.于是过点C作AB所在直线的垂线，垂足为D，考量高线的最大值(图6).此时，学生们设了各种“元”，诸如a、b、h，代数的运算举步有些艰难，磕磕碰碰、踉踉跄跄，终于也有个别学生达至彼岸，得到最大面积为3.

图6

因为h2=(2a)2-(3+b)2=a2-b2

⟹a2=2b+3,

所以h2=a2-b2=2b+3-b2=-(b-1)2+4，

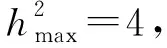
于是，出现了令人疑惑但又叫人兴奋的问题：究竟哪个答案是对的？抑或两个都不对？

解三：几何直观.满足条件的动点C在哪里？生云：圆！在线段AB上找到一点C1，使AC1=2BC1；在AB的延长线上找到一点C2，使得AC2=2BC2；以C1C2为直径作圆O，则⊙O上的任意一点C(除C1、C2外)都是符合条件的点C(图7①).

这简直是数学家的行为.此时的点C1、C2如英雄一般地做了先行者，最后却急流勇退，但是功不可没.

师问：你是怎么想到的呢？

生答：猜的.(众生笑)

师再问：如何证明就是此圆呢？

生再答：简单！根据作图所得数据，通过相似很快就能得证(图7②)……

最令人释然的是，彼时彼刻，解一的错误已昭然若揭(图7③).

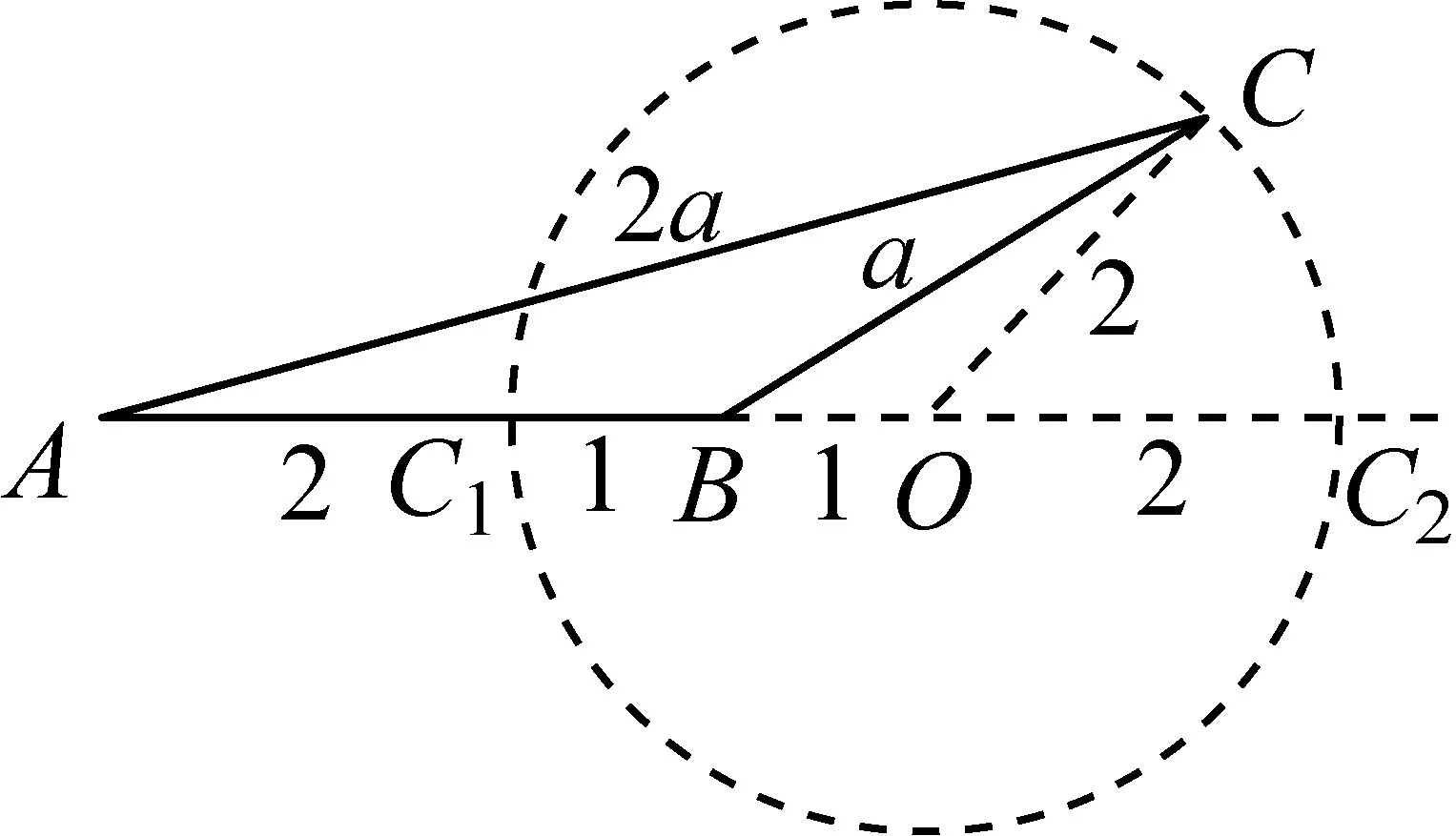
图7①

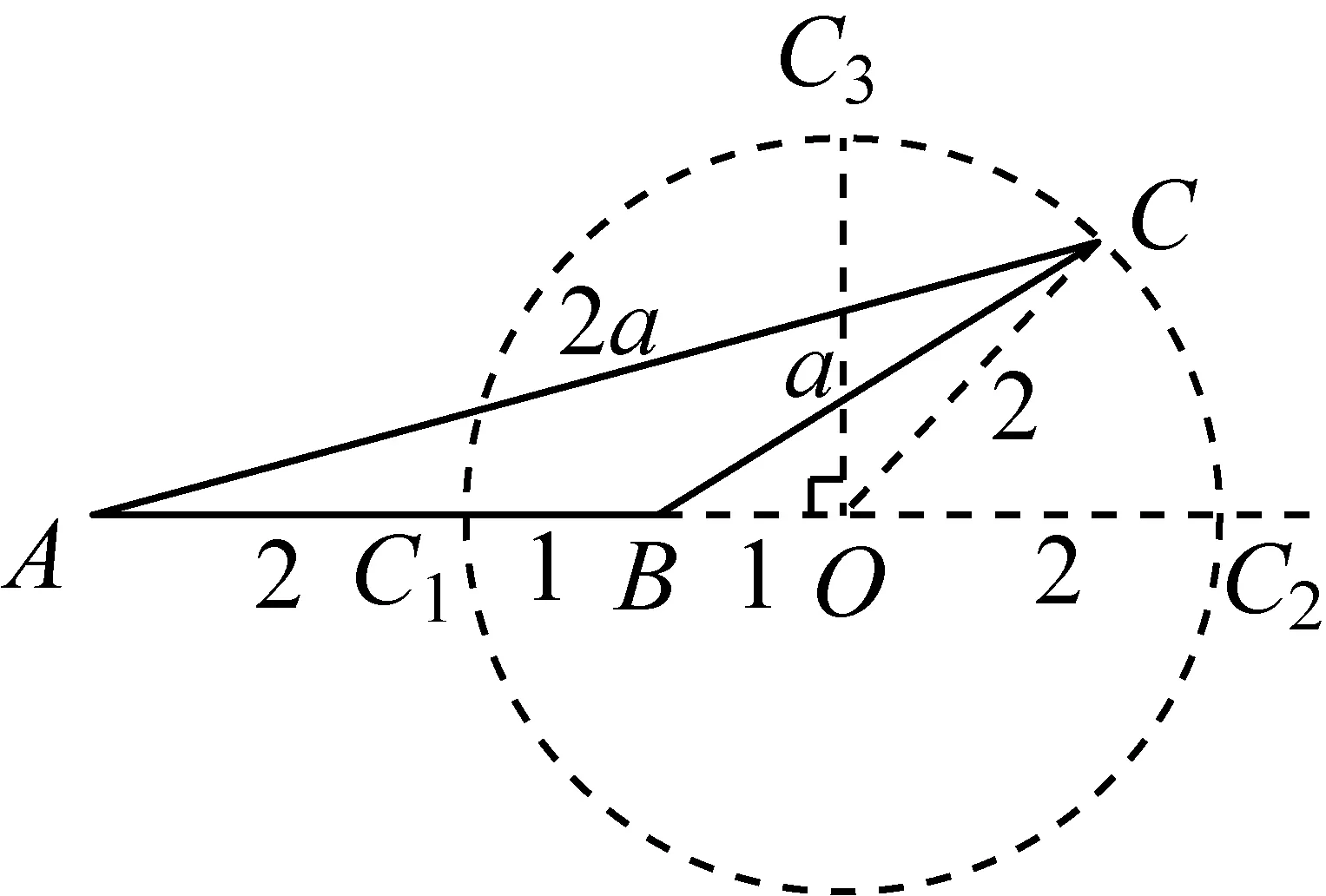
图7②

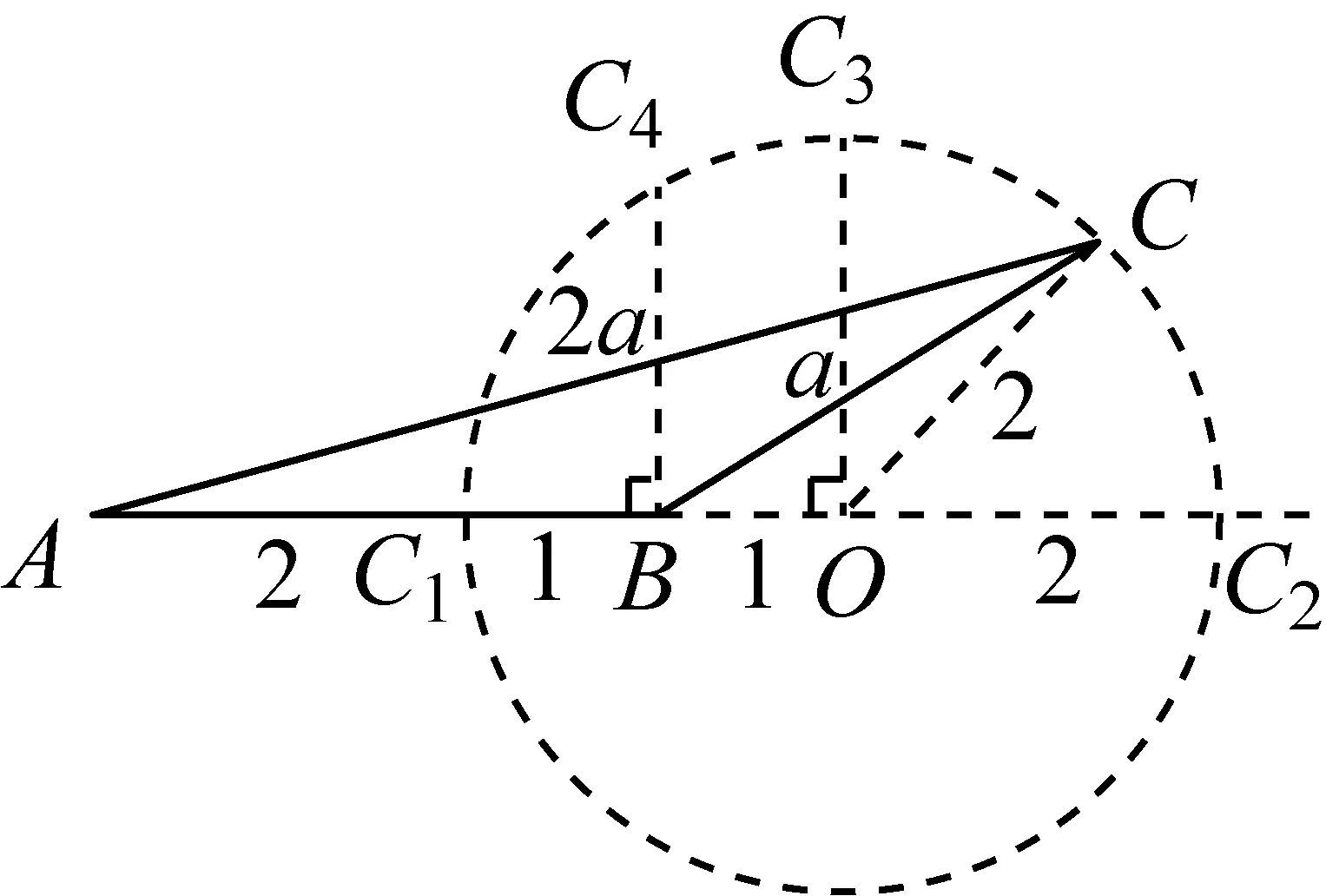
图7③

错误让学生触动良多：根据经历和经验归纳得到模型与范式，有时确实能够事半功倍，但是成也萧何、败也萧何，惟有追本溯源，回归数学本质，才是数学学习和研究的自然之道.

但是，这个圆很难想到，数学家的行为并非人人拥有！如何让思维来的更自然一些？

解四：解析法.解析法可以让学生们确确实实看见那个圆(图8).

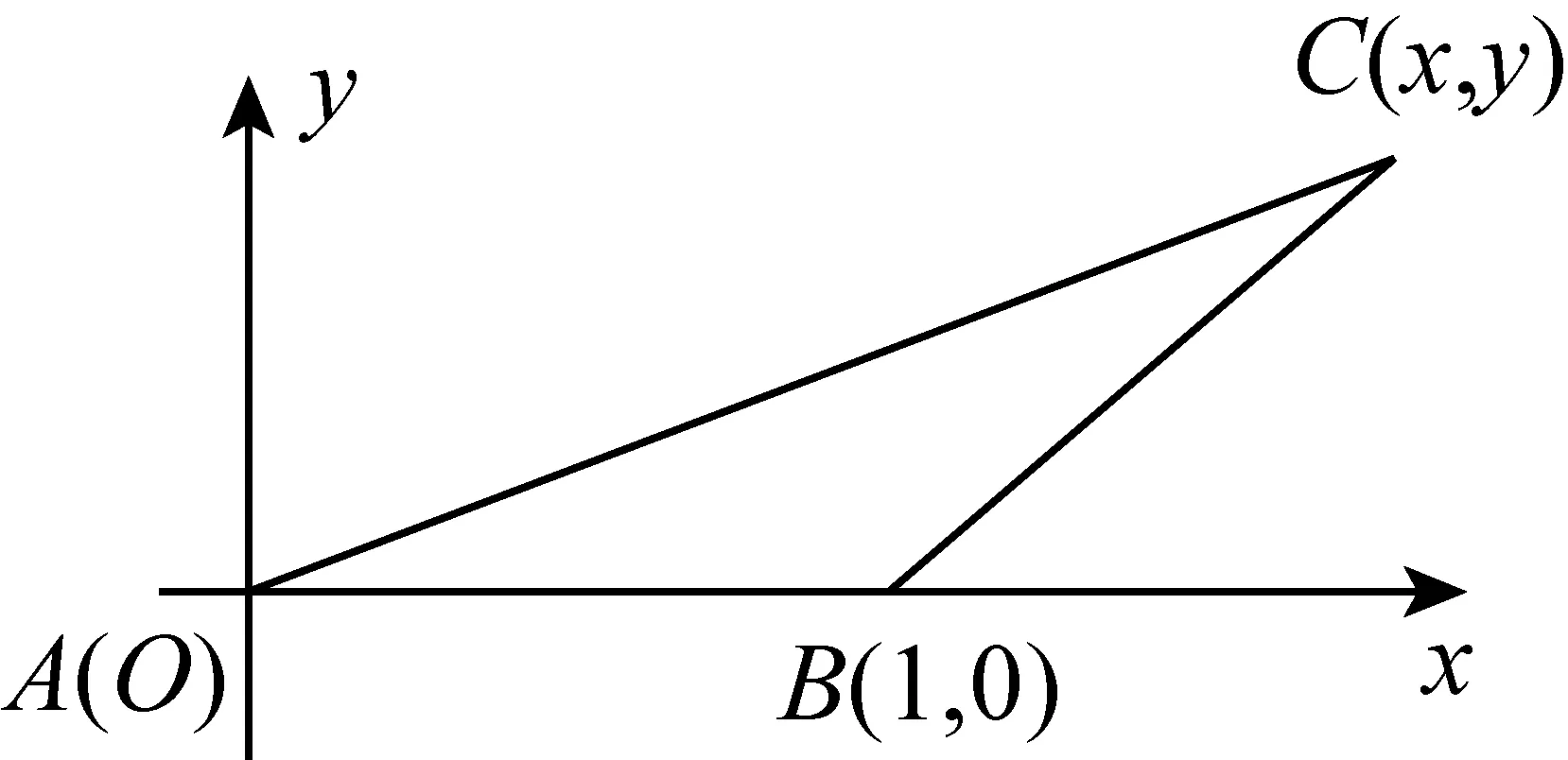
图8

因为AC=2BC⟹AC2=4BC2

⟹x2+y2=4(x-3)2+4y2

⟹x2+y2-8x+12=0

⟹(x-4)2+(y-0)2=22，

所以由两点间距离公式可知：点C(x,y)就在以点(4,0)为圆心，半径为2的圆上.

解五：海伦公式.事实上，此法与作高法在本质上是一致的.

也有一些思考与感悟，师生们共同归纳与分享.

(1)模型与范式的窠臼：无模胜有模，无招胜有招，达至“乘物以游心”之境.

(2)圆？为什么是圆？怎么想到是圆？

傅种孙先生在《高中平面几何》的自序中说：几何之务，不在知其然，而在知其所以然；不在知其所以然，而在何由以知其所以然？

(3)如何让数学经典(mathematics classical)营造出意蕴悠然的磁场，散发出引人入胜的气息，令孩子们流连忘返、兴趣盎然、欲罢不能，此乃数学教师的责任担当.

2.3 拿破仑的尺规作图问题

拿破仑的尺规作图问题，出现在浙教版初中数学教科书九年级上册第3章第7节作业题6：只准使用圆规，将一个已知圆心的圆周四等分.

传说这是拿破仑向全法国数学家发出的挑战；2018年浙江省湖州市中考试题第9题中说拿破仑向他的大臣发问；也有说是意大利数学家马歇罗尼向拿破仑提出的问题.其实这些都无关紧要，有趣味的是叱咤风云、雄霸欧洲的枭雄拿破仑，居然与几何作图相干，几何作图令其着迷.

由此引发，笔者抛给学生一个非常简单的问题：我们怎样找到一条线段的中点？

刚上初一的儿童会问：老师，这条线段软不软，可以折吗？一对折中点就有了.当然，还可以用刻度尺.老百姓都知道的方法.

进入初三的少年，断然不会这样问，他们通常不假思索地直接告诉你：尺规作图.

对于尺规作图，2000多年前古希腊数学家欧几里得在他的巨著《几何原本》中做了严格的说明.古希腊数学家非常有意思，他们认为几何作图要对作图工具进行限制，否则就不易看出谁比谁更聪明.

现在，我们将作图工具进行改变和限制：用一副刻度模糊的三角板作线段的中点(图9).

图9

用这副三角板推平行线任作一条直线MN∥AB；在直线AB、MN的同一侧任取一点P，连结PA、PB，分别交直线MN于C、D；再连结AD、BC，相交于点E；画射线PE交线段AB于点O，点O就是线段AB的中点.

师问：可以联想什么数学知识和方法来求证？(平行线-相似-对应边成比例-代数变形等)

好，我们继续将作图工具进行改变和限制：只用一个圆规.

一个圆规能干什么呢？你连一条线段也画不了，不信试试看.

中国科学院院士张景中先生在他的《数学家的眼光》以及《数学杂谈》中有生动的叙述：

法1：直接拿圆规两脚中带笔头的尖脚画线(众生笑)；

法2：固定圆规两脚中的一个针脚，迅速向外拉另一个带笔头的脚(众生又笑)；

法3：既然尺规作图圆规的半径无穷大，就以无穷大的半径画短短的一段弧，就像人站在地球表面貌似平面一样(众生疑虑重重，可信吗？)；

哈，当然，欧几里得老先生是绝对不许你这么干的.

法4：在普通的圆柱形茶缸底部放一个不大不小的圆卡片，再在茶缸内壁贴一张纸，把圆规的针脚扎在圆卡片的中心，在内壁的纸上画圆，画好后把纸揭下来看看，所画的圆变成了直线段(嗯嗯，众生颔首称道).

好吧，来看看，如何只用一个圆规平分线段(图10)？只要作6个圆即可(众生赞叹).

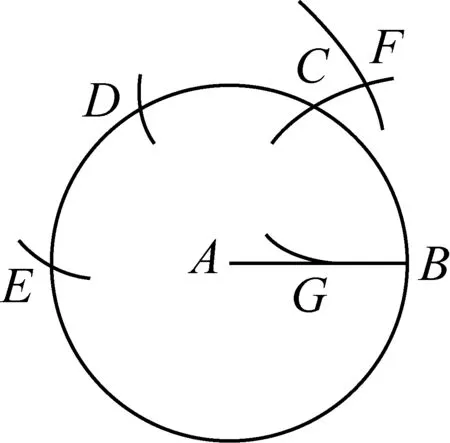
图10

当然，师仍要问：可以联想什么数学知识和方法来求证？(相似-对应边成比例)

好，现在，更厉害的来了！

上个世纪80年代，美国几何学家、年逾七旬的丹·佩多(Daniel Pedoe)在加拿大的一份杂志《数学问题》上，提出“锈规作图”.如果圆规生锈了，张不大，合不拢，只能画半径固定的圆，用它还能解决怎样的几何作图问题呢？

张景中先生给出了趣题一则：你能用半径固定(半径为1)的圆规，画一个半径为1/2的半圆吗？这个问题过于离奇，看来是不可能的.但是，别着急，一起来看看(图11)，真不错，墙上的这个半圆就是半径为1/2的圆.

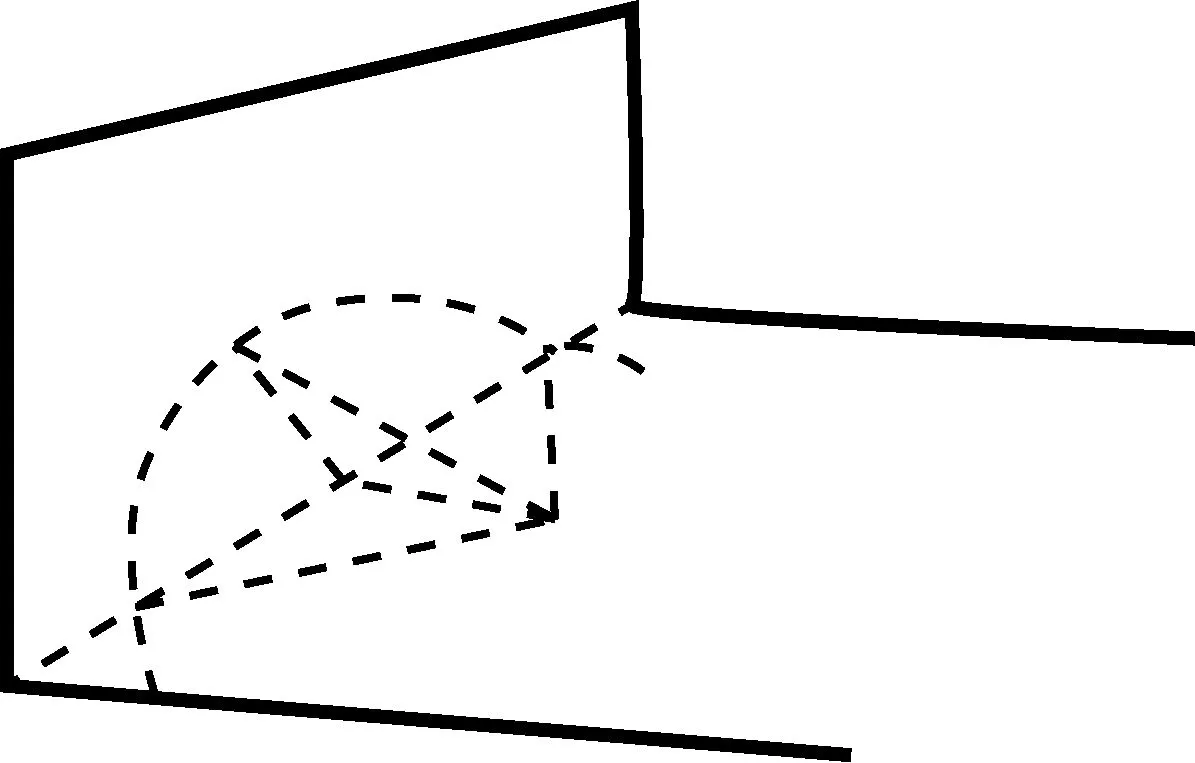
图11

当然，欧几里得老先生还是不许我们这么干的.

张景中先生给出了趣题再一则：训练有素的芭蕾舞演员，每跳一步，两脚尖的距离不多不少总是1米.你能不能帮她设计一套舞步，使她从A点出发，准确地到达B点呢？

不妨想象我们的圆规就是这样一位芭蕾舞演员.(优美的芭蕾舞演员被我们想象成冰冷的圆规，而且还是生了锈的.)

教师总是喜欢要问问学生们：你们怎么想？

生答：这回真的很困难，没有想法、没有思路.

有几名学生终于忍不住发问：A、B两点在哪里啊？

这是一个多么好的问题啊！好，如果AB恰好等于r，即AB=r，那么一步到位；如果AB

接着，可以来看看佩多教授究竟提出了怎样的两个问题：

(1)已知A，B两点，只用一个定圆规求一点C，使△ABC是正三角形.

(2)已知A，B两点，只用一个定圆规，找出线段AB的中点.

前者：张景中先生和他的搭档杨路圆满地解决了.

后者：当时我国的一位自学成才的数学爱好者侯晓荣用代数方法解决了，张景中和杨路又进一步完善了它.

更有一些思考与感悟，师生们共同归纳与分享.

(1)欧几里得的尺规作图、佩多的紧圆规、甚至柏拉图的松圆规……分析问题和解决问题的过程，令我们师生享受到思考和探究的快乐；但是，发现问题和提出问题的过程，更令我们师生们领略到数学家们的想象力和创造力的强大.

(2)波利亚《怎样解题》中有一个有趣的蘑菇原理：“好题目和某种蘑菇有点相似.它们都成串生长.找到一个后，别急着走开，四处再看看，很有可能在附近又能找到更多的.”

(3)英国数学家哈代在他的《一个数学家的辩白》中这样说：数学家在所有人里应该是最容易“出世”的.当世界疯狂时，一个数学家可以在数学中发现一种无与伦比的镇静剂.

那是一个澄明、有趣、引人入胜的数学大磁场！科学的信仰、无限的遐想……

3 结语

好的例题教学是照亮学生解题的灯塔！

臧华老师的这座灯塔，照亮了学生遨游其间的数学海洋，并将学生从题海中解放出来，使学生“爱其学而亲其师，承其难而知其益”；陈延付老师的这座灯塔，照亮了学生数学学习的征途，促进学生对数学问题本质理解能力的进一步提升，促进学生数学探索精神的进一步提升，促进学生数学素养的进一步提升；而笔者的这座灯塔，希冀能够照亮、点燃学生们在数学学习上的好奇之心、探究之意、品赏之乐，在思辨、质疑、专注、自律中，一步一个脚印地走上科学之道，并由此，享受罗素形容为冷而严肃的数学之美，领略由智力满足带来的深层次的快乐；生发一种超越世俗的平和的新的情感，养成一种善于独立思考、不怕失败、勇于坚持的新的性格.