基于有限穿越可视图的股票数据研究
2020-09-23向长城
祝 嘉,向长城
(湖北民族大学 数学与统计学院,湖北 恩施 445000)
金融领域通常被认为是一个典型的复杂系统,股票市场作为金融领域的重要组成部分,上市公司的股票价格波动便是其中的一个典型代表.股票价格波动不仅对投资者、实体经济产生巨大影响,也给监管当局带来严峻挑战,所以对股市的结构特征进行研究是有必要的[1].
时间序列研究主要囊括了几个方面:时序数据的变换、数据可视化、时序模型建立等[2-7].时间序列中的分析方法主要有自回归(AR)和移动平均理论模型(MA)、自回归条件异方差模型(ARCH)、广义自回归条件异方差模型(GARCH)等[8-13].Lacasa等[14]提出可视图理论,将每个数据点定义为节点,数据点对之间满足可视性准则记作连边,直观的转化成复杂网络;周婷婷等[15]在可视图基础上定义了有限穿越视距,引入了有限穿越可视图理论,一定程度上克服了可视图的局限性,具有更强的抗噪声能力.再利用复杂网络中已有的一些理论对时间序列进行研究,如Renyi以及Erdos建立的ER随机模型[16],Strogataz和Watts构造的小世界(small world)复杂网络[17];Barabasi和Albert发现节点的度分布服从幂律分布,即BA无标度网络特性[18].由此使得,通过可视图理论转化成复杂网络的方法对于挖掘时间序列中隐含信息具有十分重要的指导意义[19-20].
股票数据是典型的时间序列数据.目前有很多基于股票数据的研究,主要分为三类:第一类是从股票波动的角度研究其结构及动力学特征[21-23];第二类是建立股票模型及预测方法,如最小生成树(MST)、平面最大过滤图(PMFG)等[24-25];第三类是在重大事件下研究股票内部及外部成员间的相互作用和影响[26-28].本文利用有限穿越可视图理论将股票数据以网络形式呈现,借助网络的分析方法来计算度分布、聚类系数以及介数来分析时间序列特征.研究发现,股票数据转换后的复杂网络度分布也满足幂律特征和小世界特性.同时本文还通过有限穿越可视图对相关数据进行了较为准确的预测.
1 时间序列可视图模型
1.1 可视图理论
给定单变量时间序列{yi|i=1,2,3,…,N},其中yi是时间i的观测值,每个柱形的高度与时间i的数据值yi相对应,如图1(a)所示.如果ya和yb在时间序列中彼此可见,那么任意一个点yj,满足可视性准则:
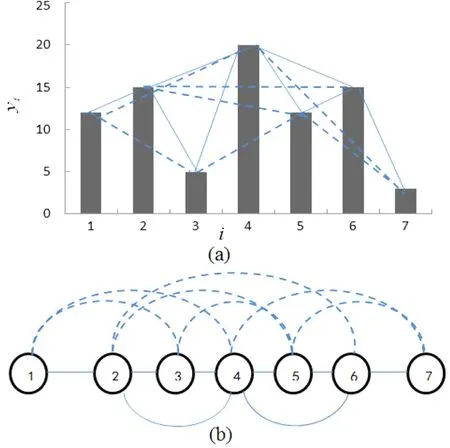
图1 有限穿越可视图Fig.1 The limited penetrable visibility graph
(1)
将时间i定义为节点,数据点对之间满足可视性准则的连线定义为边,从而构成复杂网络.可视图方法生成的网络具有以下性质:
1) 每个节点至少和它的相邻节点依次连接;
2) 节点连接之间没有方向性;
3) 横纵坐标经过仿射变换后,对应的可视图不会改变.
可视图理论“继承”了时间序列的一些特征,即不同的时间序列转为不同类型的网络;周期性时间序列转化为规则网络、随机时间序列转化为随机网络、分形时间序列转化为无标度网络[29].
1.2 有限穿越可视图理论
基于可视图理论,周婷婷[15]考虑了在可视范围内的穿越概念,提出了有限穿越可视图模型.该方法仍基于可视性准则,其原理是定义了有限穿越视距N,网络中任意两节点可视,当且仅当与两节点对应的直方条被位于其两者之间的其他直方条截断的次数n≤N.如图1为一个有限穿越可视图(有限穿越视距N=1)建网例子.
图1(a)中实线表示基于可视性准则的连线,虚线表示基于有限穿越视距N=1的新增连线.图1(a)中的七个时间点的柱形记作7个节点,满足可视性准则和在有限穿越视距N=1范围内各点间的相互连接关系构建复杂网络图,如图1(b)所示,图1(b)中节点编号上方为新增连线,下方为基于可视性准则的连线.有限穿越可视图仍然具有连通性、无向性、仿射不变性等特点,有限穿越可视图模型具有更大的连接性,抗噪声干扰能力比可视图更强.
2股票数据有限穿越可视图分析
实验数据来自于大智慧交易软件,选取2017-01-03—2018-12-31时段(节假日除外,股票市场不进行交易)标普&500指数(美国)、富时马拉西亚指数(马来西亚)、瑞士SMI指数(瑞士)、比利时20指数(比利时)、中国上证指数(中国)、意大利富时指数(意大利)6个国家的股票每日收盘价,分别建立6个国家的股票数据有限穿越可视图(有限穿越视距N=1),如图2所示.
2.1 度分布
度用来描述网络中节点的特性,节点i连接的所有边数称为该节点的度,用ki表示:
(2)
其中n是节点总数,dij=1表示节点i和节点j相连,若两节点不相连则dij=0.
在网络中随机抽取到度为k的节点的概率为pk,Nk是度为k的节点数,
(3)
(4)
图2中6个网络度分布如图3所示,6个网络其他相关指标如表1所示.
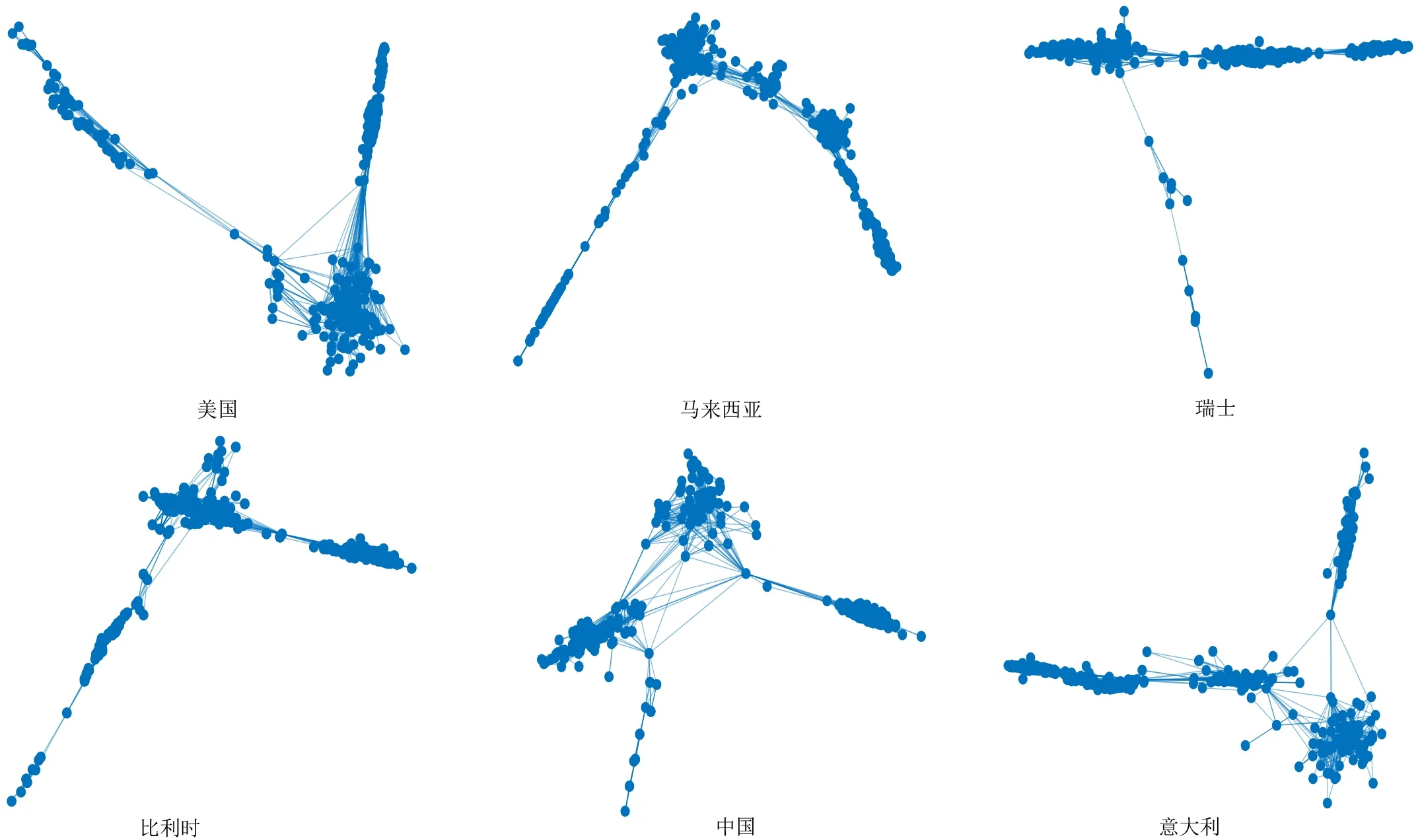
图2 6个国家股票数据有限穿越可视图(2017-01-03—2018-12-31)Fig.2 Limited penetrable visibility graph of stock data for six countries (from Jan.3,2017 to Dec.31,2018)
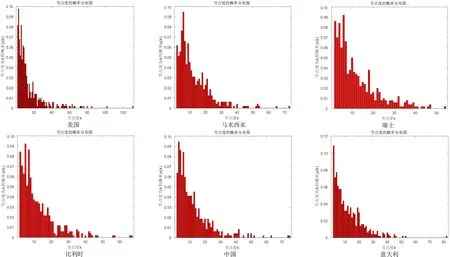
图3 度分布概率图Fig.3 Probability map of degree distribution
从图3可以看出,6个网络中度值较小的点概率比较大,度值较大的点比较少,都呈现幂律特性.结合图3、表1可知,美国股票网络的最大度值高达131,其余5个网络最大度值在50~80之间,由股票数据可知,美国股票每日收盘价在2018-09-20日达到最高值2 930.75,这促使了大度节点的出现.方差与标准差可以反映数据的离散程度,取值越大,说明这个时间序列越不稳定,而从中可看出美国股票网络的标准差和方差取值较大.观察实际数据发现,美国股价从2017-01-03日2 257.83到2018-02-05日为2 648.93,再到2018-09-20日增至2 930.75,而2018-12-24日下跌至2 351.1,呈现时间短且变化快的特点,使得该网络度分布波动较大.据搜狐2018年12月28日发布的《每日经济新闻》分析美股下跌这其中可能的原因是美联储官员们的讲话引发了投资者对美联储加息节奏的猜测,引发了市场恐慌情绪,同时市场对美股企业盈利的担忧、美国疲弱的房屋销售数据等因素也导致了大跌.
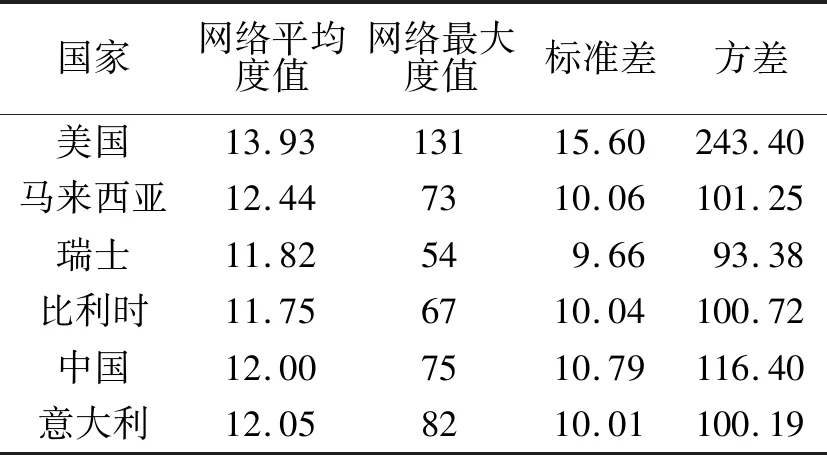
表1 网络相关指标比较Tab.1 Comparison of network related indicators
2.2 小世界特性
如果一个网络比同规模的随机网络表现出了较大的聚类系数和较小的平均路径长度,就称该网络具有小世界特性[14].对于给定的节点i,其聚类系数Ci表示为:
(5)
与节点i连接的ki条边,ki个节点最多有ki(ki-1)/2条边,Ei表示ki个节点实际存在的边数.网络的平均聚类系数C定义如下:
(6)
在连通节点i和节点j的所有通路中,途经其他顶点数目最少的路径称为dij,平均路径长度L定义为任意两节点之间最短路径的平均值:
(7)
股票数据构造的6个有限穿越可视图网络每个节点的聚类系数分布情况,如图4所示(横线表示网络平均聚类系数所在直线).平均聚类系数、平均路径长度、最短路径最大值三项小世界特征指标,如表2所示.

图4 聚类系数分布情况(横线为网络平均聚类系数值)Fig.4 Distribution of clustering coefficient (The horizontal line is the C of the network)
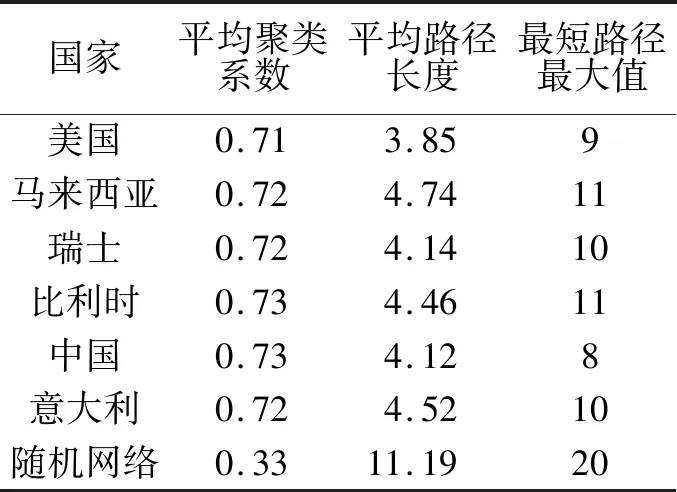
表2 小世界特征指标Tab.2 Small world characteristic index
从图4可知6个网络中Ci为1的节点较多,Ci的值偏大.由表2可知,6个网络的平均聚类系数C集中在0.7~0.8之间,平均路径长度集中在3~4之间.用Pajek实验10次生成同等规模的502个节点构成的随机网络,得到平均路径长度为11.19,平均聚类系数为0.33,比较可知6个网络的平均路径长度明显小于随机网络,而聚类系数均高于随机网络,6个网络都是典型的小世界网络.
2.3 介数
介数是网络中一种重要的全局几何量,反映了节点在整个网络中的影响力.如果节点i被其他许多最短路径经过,则表示该节点在网络中的重要性,介数Bi表示为:
(8)
Njk表示节点j和节点k之间的最短路径条数,Njk(i)表示节点j和节点k之间的最短路径经过节点i的条数.6个网络的最大介数、平均介数如表3所示.
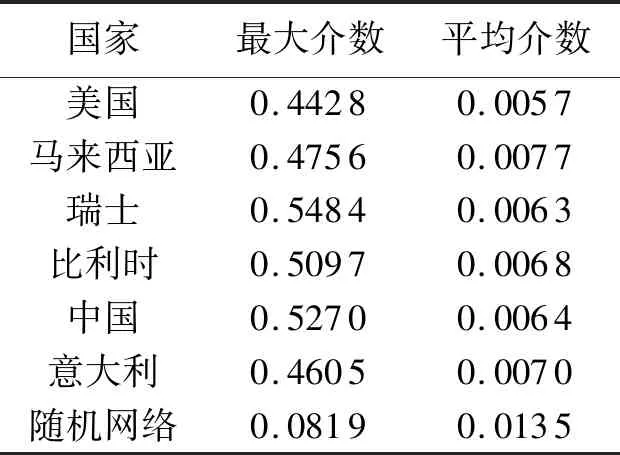
表3 介数指标Tab.3 Betweenness index
由表3可知6个网络的最大介数在0.4~0.5之间,平均介数在0.005~0.007之间,而用Pajek实验10次生成同等规模的502个节点构成的随机网络得到的最大介数为0.081 9,平均介数为0.013 5,比较发现6个网络的介数值与随机网络差别较大,出现这种情况的可能原因是6个网络中都有大量hub节点的出现,这反映该时段股票均存在异常高值现象.
3 有限穿越可视图在股价预测中的应用
当预测时间序列中某节点的值时,如果估算出该节点的度值,便可以通过计算任意一对数据点之间的斜率来推算该节点所处的区间[18].为了直观的说明有限穿越可视图在股票价格预测中的应用,选取中国上证指数2018-12-10—2018-12-14股票每日收盘价格,这5天股票每日收盘价格柱形图如图5所示,再将股票数据转化为有限穿越可视图(有限穿越视距N=1),如图6所示.
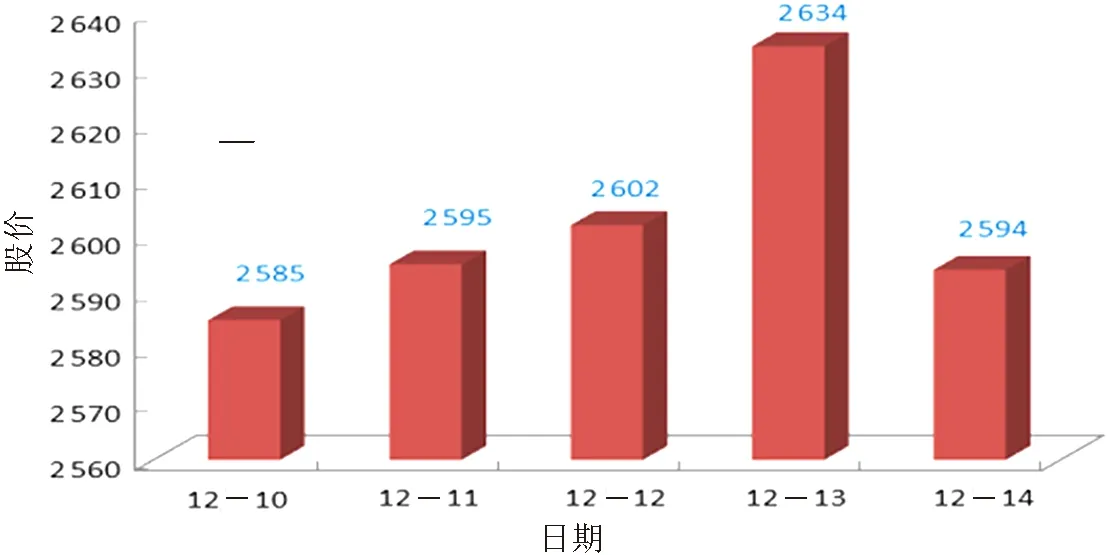
图5 中国5日股价柱形图Fig.5 Column chart of China’s 5-day stock price
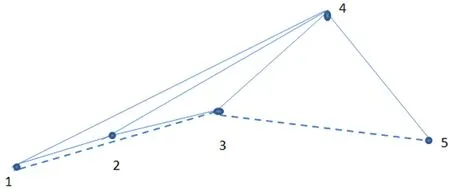
图6 中国5日股价有限穿越可视图Fig.6 China’s 5-day stock price of limited penetrable visibility graph
如果预测第六个节点(2018-12-17,星期一)的股票收盘价格,分以下几种情况讨论:①如果估算第六个节点的度值为1,显然只有第六个节点与第五个节点(2 594)相连.按可视化准则计算第六个节点被第四个节点(2 634)看见,则预测值要大于2 554,如果预测值小于2 554时,则根据有限穿越可视图(有限穿越视距为1)理论,第六个节点可以被第四个节点看见,此时第六个节点度值为2,故第六个节点度不可能为1.②如果估算出第六个节点的度值为2,因为第六个节点与第五个节点肯定相连,从图6知第五个节点的度值为2,分别与第四个节点、第三个节点(2 602)相连,第四个节点的度值为4且数据值最大,所以第六个节点最有可能与第四个节点相连,故第六个节点的预测值必然在第五个节点和第四个节点之间的斜率之上,即大于2 554;若第六个节点的值高于第四个节点,则会被第三个节点在有限穿越视距范围内看见,故第六个节点度为2时,预测值范围为[2 554,2 634].③如果估算出第六个节点的度值为3,则第六个节点可能与第五个节点、第四个节点、第三个节点相连,第六个节点的预测值所处区间为[2 554,2 698].④如果估算出第六个节点的度值为4,则第六个节点可能与第二个节点(2 595)、第三个节点、第四个节点、第五个节点相连,则第六个节点的预测值所处区间为[2 554,2 673].⑤如果估算出第六个节点的度值为5,则第六个节点可能与第一个节点(2 585)、第二个节点、第三个节点、第四个节点、第五个节点相连,则第六个节点的预测值所处区间为[2 554,2 667].
综上所述,预测值为区间[2 554,2 634]、[2 554,2 698]、[2 554,2 673]、[2 554,2 667]的交集,故第六个节点的预测区间为[2 554,2 634],而实际值为2 598,满足条件.
如果预测第七个节点(2018-12-18,星期二)的股票收盘价格,则把第六个节点(2018-12-17,2 598)当成已知数据,重复以上步骤,分以下几种情况讨论:①如果估算第七个节点的度值为1,显然只有第七个节点与第六个节点(2 598)相连.按可视化准则计算第七个节点被第四个节点(2 634)看见,则预测值要大于2 580,如果预测值小于2 580时,则根据有限穿越可视图(有限穿越视距为1)理论,第七个节点可以被第四个节点看见,此时第七个节点度值为2,故第七个节点度不可能为1.②如果估算出第七个节点的度值为2,计算出预测值区间为[2 580,2 634].③如果估算出第七个节点的度值为3,此时预测值区间为[2 580,2 602].④如果估算出第七个节点的度值为4,预测值所处区间为[2 580,2 597].⑤如果估算出第七个节点的度值为5,预测值区间为[2 580,2 599].⑥如果估算出第七个节点的度值为6,预测值范围为[2 580,2 600].
综上所述,预测值为区间[2 580,2 634]、[2 580,2 602]、[2 580,2 597]、[2 580,2 599]、[2 580,2 600]的交集,故第七个节点所处预测区间为[2 580,2 597],而实际值为2 590,满足条件.
根据以上两个例子可知,能准确估算出要预测的时间节点的度值,便可以确定该节点所处的区间,所以要预测的节点实际数值与其度值紧密联系.
4 结论
本文基于股票数据这一主题,通过有限穿越可视图理论将时间序列转化为复杂网络并分析其网络拓扑特征.结果表明股票有限穿越可视图网络具有小世界特性、度分布服从幂律分布等特点,也揭示了股票的部分特征.文中将股票时间序列数据转为有限穿越可视图网络研究并进行了较为准确的预测,试图为监管当局、经济市场提供一定的理论支持和实践基础.
