透过现象看本质——对一道浙江模拟试题的思考

陈 艳

浙江省安吉县昌硕高级中学 (313301)

在2020年3月浙江十校联考考试中，出现一题平面向量的填空题，题目如下：

下面介绍对这道试题分析解答过程，供大家参考．

1.剔除包装，显现问题本质

由于试题要计算平面向量的模，所以在解题中许多同学选择“见模平方”的原则，得到：

点评：难题之所以是难题，往往有以下两方面的原因；其一是命题者对试题进行了过度的“包装”，使考生感到“雾里看花，水中望月”，看不清问题本质；其二是试题对学生的数学能力要求较高，所以对过度“包装”的试题，首先要做到的是剥去过度的“包装”，暴露问题本质.

2.采用坐标，强攻向量模长

不难发现，把本题放入直角坐标系中进行研究，然后按部就班进行推算即可，其解题对策好比排球比赛中的高点强攻战术.

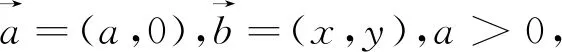
点评：建立坐标，得到目标函数的方法是解决几何图形中最值问题常用方法之一，本题解法的解题思路自然，容易上手.

3.巧设坐标，优化解题过程

在上述坐标运算中，整体计算还是有点繁琐，那么我们思考：在坐标的设法中，有没有更加巧妙的处理方法呢？

4.合理配凑，简化计算量度

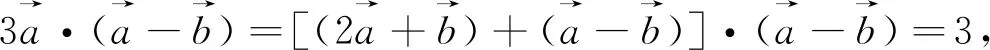
5.巧用换元，揭示几何背景

我们知道很多向量问题，都有一定的几何背景，但是本题从题干很难看出它出自何背景，因此我们需要先做一定处理，即换元.

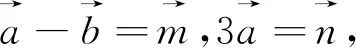
图1

点评：巧用换元，揭示几何背景即考查点与圆的位置关系.

6.发散思维，取三角不等式

点评：在向量模问题中，绝对值三角不等式不失为一种好的方法，但它对思维要求较高，也比较难以掌握.

7.反思总结，再结累累硕果

对于浙江高考平面向量问题，不外乎上述所述的一些方法，如果能够很好的掌握上述方法，平面向量问题将能够迎刃而解.最后我们在练习一道最新的模拟试题.

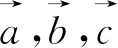
本题解法同上题，本文在此不再累赘.