GNSS实时卫星钟差估计技术进展
2020-09-23黄观文王浩浩
黄观文,王浩浩,谢 威,曹 钰
(长安大学地质工程与测绘学院,西安 710054)
0 引言
全球卫星导航系统(Global Navigation Sate-llite System,GNSS)是能在地球表面或近地空间的任何地点为用户提供全天候的三维坐标和速度以及时间信息的空基无线电导航定位系统[1-2]。中国自主建设、独立运行的北斗三号全球卫星导航系统(BeiDou Navigation Satellite System,BDS)已于2020年7月31日正式开通,标志着我国成为世界上第3个独立拥有全球卫星导航定位系统的国家。目前,天空中已有超过100颗GNSS工作卫星,迈入到一个多星座多频率数据融合的新时代。
GNSS测量的基本原理是利用伪随机噪声码进行时间比对,得到测距信号的时间延迟[3]。因此,精确的位置测量实际上就是精确的时间测量。星载原子钟作为导航卫星的时间基准,也是卫星导航系统有效载荷的核心,其性能直接决定着定位、导航与授时(Positioning,Navigation and Timing,PNT)的服务质量[4]。星载原子钟利用原子能级跃迁的频率来精确计量时间时造成卫星钟的钟面时与标准时间的差异,即卫星钟差。精密卫星钟差的获取对GNSS实现高精度服务性能具有重要的实践价值。
本文首先简单介绍了卫星钟差产品的类型和特点,然后系统概述了实时卫星钟差估计技术的进展、关键方法以及与实时钟差预报技术的关系,最后讨论并展望了目前所面临的技术挑战。
1 GNSS实时钟差技术发展
精密卫星轨道和钟差产品是实现GNSS高精度PNT服务的先决条件,其精度决定了GNSS的服务性能[5],目前国际GNSS服务组织(International GNSS Services,IGS)提供的最终卫星钟差产品精度为75ps,能够很好地满足用户事后高精度定位的需求(http://www.igs.org/products),但需要延迟12~18天才能获取;即使是精度略差的快速钟差产品也存在17~41h左右的时延,已无法满足用户对于时效性的要求。因此,用户一般采用广播星历来满足实时性的需求,但目前广播星历的卫星钟差精度较低,大约在5ns左右。为此,IGS还提供了可用于实时定位的超快速钟差产品,该产品时间弧段为48h,前24h弧段的实测钟差精度优于0.15ns,但仍存在3~9h的时间延迟;后24h弧段预报部分可以满足实时应用的需求,但由于在轨星载原子钟极易受外界环境及自身因素的影响,变化极为快速复杂,难以用数学模型进行准确预报[3],其只能达到略优于广播星历的钟差精度3ns左右,远远低于IGS建议的实时卫星钟差精度0.3ns,仍不能满足实时高精度定位的要求。因此,高精度的实时卫星钟差必须利用地面跟踪站网的实时观测数据进行GNSS实时卫星钟差估计[6]。
鉴于广播星历和超快速产品的钟差精度均难以满足用户实时高精度导航定位的需求,IGS实时工作组从2007年开始启动实时实验项目(IGS Real-Time Pilot Project,IGS-RTPP),并在2013年实现了一套完整的实时产品服务(Real-Time Service,RTS)系统,将实时卫星钟差改正数采用状态空间表达(State Space Representation,SSR)信息格式,基于互联网进行RTCM网络传输的协议(Network Transport of RTCM over the Internet Protocol,NTRIP),通过互联网的方式向全球用户播发[7-8]。多家GNSS分析中心与组织也开始致力于实时精密卫星钟差估计的算法研究与产品生成,如德国联邦制图与大地测量局(Bundesamt für Kartographie und Geodäsie,BKG)、法国空间研究中心(Centre National d’Etudes Spatiales,CNES)、德国波茨坦地学研究中心(Deuts-che GeoForschungsZentrum, GFZ)和中国武汉大学(Wuhan University,WHU)等。目前,绝大多数IGS分析中心提供的实时钟差产品都是5s更新且精度大致相当,在0.2ns左右[9]。
在卫星钟差估计方面,主要分为早期的GPS实时卫星钟差估计和后续的GNSS实时卫星钟差估计。在GPS实时卫星钟差估计方面,Zhang等使用Auto-BAHN软件,采用扩展Kalman滤波(Exten-ded Kalman Filter,EKF)的估计方法,实现了近实时GPS轨道和钟差的确定[10];Mevart等仅利用历元间差分载波相位观测值,实现了GPS实时卫星钟差估计[11];楼益栋首先分析了伪距和相位观测值对钟差估计的影响,然后在实时估计过程中通过参数引入与消除的方法减少待估参数的个数,加快数据处理速度[12-13];Hauschild和Montenbruck基于非差观测量,采用Kalman滤波实现了近实时GPS卫星钟差估计,并将其应用于低轨卫星定轨[14];Bock等利用历元间差分模型对非差估计5min间隔的卫星钟差进行加密,然后通过线性内插得到了1Hz高频卫星钟差[15];李星星等实现了基于非差载波相位观测值的实时GPS精密卫星钟差估计算法[16];李浩军等采用历元间、星间差分技术消除了模糊度和接收机钟差参数,进而快速求解出相邻历元间相对钟差的差值[17-18];Zhang等采用非差伪距和载波相位观测值、历元间差分伪距和载波相位观测值并行计算的方法,实现了GPS实时精密卫星钟差估计算法[19];基于对流层延迟短时间内几乎不变的特性,宋伟伟提出了在实时卫星钟差估计中采用对流层双线程处理策略来提高解算效率[6];Ge等于2012年提出了一种基于非差伪距观测量和历元间差分载波相位观测量的混合差分模型,该模型消除了模糊度参数,大幅度提高了解算效率,估计得到的卫星钟差精度与非差模型的结果精度相当[20]。
除了上述针对GPS实时钟差的研究外,目前也有大量学者对GNSS实时钟差估计算法进行了探索。Fu等推导了轨道误差对实时钟差估计的影响模型,分析了不同轨道精度下BDS实时卫星钟差的估计精度[21];赵齐乐等实现了基于非差观测量GPS/BDS组合实时钟差估计算法,估计得到的BDS实时钟差精度优于0.15ns[22];基于Ge等提出的混合差分模型,GPS/BDS实时卫星钟差联合估计算法得以实现[23-24]。随着GNSS卫星和地面跟踪站数目的不断增加,解算效率和实时性是目前实现多模GNSS实时高频卫星钟差估计所要面临的重要问题。Chen等在混合差分模型的基础上,通过伪距观测值星间差分进一步消除了接收机钟差参数,在保证卫星钟差精度的基础上,进一步提高了GNSS实时钟差估计的解算效率[25-26];考虑到对流层变化十分缓慢、模糊度参数收敛后趋于常数等特点,戴志强提出了在非差方法的基础上,利用快、慢更新线程并行的GNSS实时钟差估计方法,研究表明该方法在效率和精度上都优于历元间差分方法[3,27];Ye等推导证明了实时卫星钟差估计中非差模型与混合差分模型的等价性[28];面对多模GNSS单个历元计算负荷大的问题,Gong等基于分块矩阵QR分解法,采用均方根信息滤波参数估计方法进行GNSS实时卫星钟差估计,兼顾了解算效率和精度要求[29];针对区域GNSS实时钟差估计时观测数据的不连续导致钟跳的问题,Shi等根据GNSS不同类型星载原子钟的物理特性提出了一种原子钟噪声模型,相对传统的白噪声估计,利用该模型估计的卫星钟差平均标准偏差(Standard Deviation,STD)和均方根(Root Mean Square,RMS)分别提升了44.4%和12.1%[30];Fu等设计了高阶法方程的快速解算算法,实现了基于序贯最小二乘的实时卫星钟差快速估计[31];随后,又针对GNSS组合实时卫星钟差估计中在线质量控制难、计算效率低的问题,提出了一种适合高维最小二乘下实时钟差质量控制方法[32];Liu等基于非差观测量实现了一种高效的GNSS联合实时高频(1Hz)精密卫星钟差估计方法[33];Dai等和Yang等基于非差模型提出的非差模糊度固定策略,能够提升实时钟差估计的收敛时间和卫星钟差精度,同时基于实时钟差产品进行的实时动态精密单点定位(Precise Point Positio-ning,PPP)的收敛时间和定位精度也得到了提升[34-35];Li等提出了GNSS整数恢复钟模型,恢复了模糊度参数的整周特性,研究表明该模型能够提升GNSS实时估计的卫星钟差精度和解算效率,同时也促进了GNSS实时PPP模糊度固定的应用[36];Zhao等基于混合差分模型提出了一种适用于全球/区域GNSS实时卫星钟差估计中钟差基准选择和初始卫星钟差偏差预报的策略,以避免实时钟差产品的不一致性[37]。
综上所述,随着GNSS的发展日益趋向现代化以及全球能够提供多GNSS实时数据流的地面监测站数目的不断增多,GNSS的实时高精度服务性能将受到越来越多的关注。因此,GNSS实时精密卫星钟差估计将是实时精密数据处理的研究重点,也是实现高精度实时定位的关键技术。
2 GNSS实时钟差估计技术
2.1 GNSS无电离层组合观测方程
GNSS实时精密卫星钟差估计一般是基于地面跟踪站网的双频(或多频)伪距和载波相位观测量,根据电离层延迟与信号频率的平方成反比这一特性,对不同频率的相位和伪距观测值进行线性组合以消除电离层一阶项,剩余的高阶项影响很小,一般不予考虑[38],形成的双频观测量无电离层组合观测方程如下
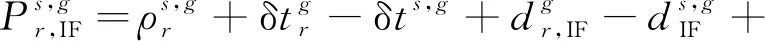
(1)

上述无电离层组合观测方程是基于f1和f2信号的观测量形成的,对于三频或多频(如GPS L1/L2/L5, BDS B1I/B3I/B1C/B2a等)信号,任意2个频率之间的无电离层组合与上述类似。
2.2 GNSS实时钟差估计技术
GNSS实时卫星钟差估计根据其采用的观测量模型的不同,可分为非差估计法、历元间差分估计法以及混合差分估计法等[8]。表1从不同实时卫星钟差估计技术的原理方法、待估参数、算法效率和优缺点及适用性等方面进行了总结。

表1 GNSS实时卫星钟差估计技术总结
2.3 实时钟差解算的参数估计方法
实时钟差解算的参数估计方法通常有序贯最小二乘(Sequential Least Square,SLS)估计、Kalman滤波(Kalman-filter,KF)估计以及均方根信息滤波(Square Root Information Filter,SRIF)估计等。
1)Kalman滤波
Kalman滤波是基于观测序列以及动力学模型信息求解状态向量的最优估值[14,43]。其观测方程和状态方程如下
Lk=AkXk+Wk
(2)
Xk=Φk,k-1Xk-1+Γk-1Ωk-1
(3)
式中,k为历元观测序列;Lk为历元k的观测值向量;Xk为历元k的状态向量;Ak为观测方程的系数阵;Wk为观测噪声向量;Φk,k-1为状态转移矩阵;Ωk-1为动态噪声向量;Γk-1为动态噪声矩阵。
对观测方程和状态方程进行线性化后,每个历元通过不断预测—修正—预测的过程估计得到新的滤波估值,且不需要存储之前历元的大量观测数据[6]。上述Kalman滤波与最小二乘估计是等价的,并可由最小二乘推导得出。
2)均方根信息滤波
SRIF作为Kalman滤波的一个演化版本,采用平方根矩阵,能够确保协方差矩阵的对称性和正定性[12]。利用Household变换避免了法方程的求逆,能够有效地克服滤波器的发散,比Kalman滤波具有更高的数值稳定性和计算高效性[44-45],但同时也增加了参数估计的复杂性。
3)序贯最小二乘估计
序贯最小二乘估计也是一种经常用于动态定位的经典方法,可避免不精确状态模型信息的影响[46]。已有研究证明,在实时卫星钟差的估计过程中,模糊度和系统间偏差等参数作为常数估计而钟差参数被模型化为白噪声。序贯最小二乘估计方法和滤波解是等效的[14,47],在GNSS实时钟差估计工作中,三种参数估计方法理论等价,可任选其一。
2.4 实时钟差预报和实时钟差估计的关系
除了实时卫星钟差估计,卫星钟差预报也是一种获取实时卫星钟差的方式。钟差预报是指利用一段已知的钟差数据进行建模,预报未来一段时间的卫星钟差。当前,常用的模型主要有:一次多项式模型、二次多项式模型、灰色模型、差分整合移动平均自回归模型和谱分析模型[48-49]。目前,已有多家分析中心提供超快速卫星钟差预报产品。表2给出了2019年8月22日—2019年8月28日共7天GFZ 的GNSS超快速预报钟差产品精度统计指标。可以看出,目前Galileo、GPS、GLONASS和BDS-2的24h超快速预报钟差精度分别为0.54ns、2.13ns、2.75ns和4.24ns。BDS-2超快速预报钟差精度较差,主要是由于BDS异构星座中的地球静止轨道(Geostationary Earth Orbits,GEO)卫星钟差精度较低导致。Galileo产品精度最优,基本可以满足分米级导航定位服务要求。本文简要总结了实时钟差估计和钟差预报的优点与不足,如表3所示。相比于实时钟差预报,实时钟差估计能够提供较高精度的卫星钟差,以及更高精度的PNT服务。然而,钟差估计需要较多的地面观测站提供实时观测数据。由于接收机性能、网络时延和通信设备等多种因素的影响,实时观测数据流的数量难以保证,甚至会出现所有测站的观测数据中断,此时钟差无法估计。为了维持实时卫星钟差数据,需要采用实时卫星钟差预报,钟差预报可以提供连续的钟差值。但是,原子钟的变化极为复杂,难以采用精确的数学模型进行建模,导致预报的钟差精度较低。

表2 GFZ超快速钟差预报精度

表3 钟差估计与钟差预报的优缺点比较
随着原子钟稳定性的提升和物理模型的精化,笔者认为中短期(24h内)实时钟差预报精度有望稳定提升至0.5ns内,未来可为用户提供分米级至厘米级的实时精密定位服务,但厘米级至毫米级的高精度实时定位仍需要实时卫星钟差估计技术的支持。
3 结论与展望
鉴于GNSS实时卫星钟差估计技术的重要性,本文首先综合现有的文献资料,对目前实时卫星钟差估计技术的研究进展和关键方法分析等方面进行了较为系统的论述。本节结合目前研究成果,对未来卫星钟差估计技术面临的挑战进行了初步展望,希望能为该方向学者下一步的研究工作提供一点参考。
1)BDS实时钟差产品的精度和可靠性是保障实时PNT服务的关键,然而目前对BDS实时钟差估计的探索和研究还主要是借鉴GPS实时钟差的处理方法。针对我国BDS空间段采用三种轨道卫星组成混合星座的特点,提出了分类控制不同星座卫星钟差的解算策略,精化了卫星钟差求解的函数模型及随机模型,但是实现厘米级高采样率高可靠性的BDS实时钟差产品,还需进行更为深入的研究。
2)在GNSS卫星钟差估计中,钟差参数通常被简单模型化为白噪声进行估计,这种简化的假设并不能严格反映钟差的物理模型。尽管实时处理卫星钟差模型噪声会增加计算负担,但是更为稳定可靠的卫星钟差产品对于GNSS的授时与时间同步尤为重要。因此,考虑不同类型的GNSS星载原子钟,建立能够正确反映卫星钟差物理特性的噪声模型,将是一项重要的精细化研究工作。
3)实时数据流的解析和处理是GNSS实时卫星钟差估计的基础工作,直接决定解算卫星钟差的精度和可靠性。受地面监测站布设位置、环境、通信设备和接收机性能等因素的影响,目前GNSS全球连续跟踪站实时数据流仍存在时延、丢包和数据中断的现象,导致观测数据质量包含较多的粗差和钟跳等异常。因此,要实现高效率高质量的GNSS实时流数据预处理与质量控制工作还面临很大的挑战。
4)数目众多的模糊度参数和不合理的对流层约束是影响GNSS实时卫星钟差解算效率和精度的重要因素。在多系统组合GNSS实时卫星钟差估计过程中,高频数据的观测值数目以及需要解算的高阶法方程维数导致计算量十分庞大。因此,如何充分利用现代高性能计算机处理器的计算能力,优化高维法方程解算算法,从而实现GNSS实时钟差的快速估计以及多系统GNSS实时钟差的融合处理还需要进一步研究。
5)目前实时钟差产品分为预报和估计两种,综合技术优缺点和目前精度指标,笔者初步建议预报钟差精度(6h)优于0.2ns时,实时产品以预报产品为主、实时估计为辅(主要提升可靠性);预报产品精度(6h)差于0.2ns时,实时产品以估计产品为主、实时预报为辅(主要提升连续性)。
