抗差自适应分步滤波算法在PPP/INS组合导航中的应用
2020-09-23张且且周建华
张且且,赵 龙,周建华,2
(1.北京航空航天大学自动化科学与电气工程学院,北京 100191;2.北京卫星导航中心,北京 100094)
0 引言
由于卫星导航和惯性导航组合可以实现优势互补,提高导航系统的定位精度和可靠性,因此全球导航卫星系统(Global Navigation Satellite System,GNSS)/惯性导航系统 (Inertial Navigation System,INS)组合导航一直是国内外学者的研究重点。近年来,随着精密单点定位 (Precise Point Positioning,PPP)技术的发展和成熟,将PPP与INS组合,即能克服差分全球导航卫星系统(Differential GNSS,DGNSS)/INS受作业距离限制的缺点,又能获取高精度的位置、速度和姿态信息,因此很多学者对PPP/INS组合进行了大量的研究工作[1]。
在PPP/INS组合导航定位中,为获取状态参数的最优估计,通常采用Kalman滤波。由于滤波器的性能受随机模型和函数模型精度的影响,因此只有二者都可靠的情况下,才能获得状态参数的最优估值。然而,在实际应用中,受各种因素的影响(例如,状态方程和观测方程存在误差,随机模型所描述的观测噪声和过程噪声通常由经验值或经验模型获得,并不能准确地反映当前系统的真实噪声水平,观测量中可能存在非正态分布的异常观测等),导致滤波器的性能有时并不理想。为提高滤波器的性能,众多科研工作者对自适应滤波技术进行了广泛而深入的研究。为解决根据先验信息确定的随机模型不能真实反映系统噪声水平的问题,提出了对系统噪声协方差矩阵进行在线估计的方法[2-3],其中Sage-Husa滤波法[2]应用最为广泛。该方法利用固定窗口内的新息或残差估计当前历元时刻的观测噪声协方差矩阵,利用预测状态残差估计当前历元时刻的过程噪声协方差矩阵[4]。虽然对噪声协方差矩阵的实时估计可以使预测残差与相应的统计量保持良好的一致性,但要获得较好的滤波效果,还需要有准确的函数模型为前提。这是因为系统噪声的估计与预测的状态参数存在耦合,当函数模型存在误差的情况下,会影响噪声协方矩阵的估计精度,导致滤波器的性能进一步下降。针对该问题,严恭敏等[5]利用Allen方差分析实现了对噪声协方差矩阵估计和滤波状态参数估计的解耦。但该方法仅适用于缓变系统,对于变化剧烈的系统,该方法的估计精度会明显变差。周启帆等[6]针对具有冗余测量的导航系统,提出了基于冗余测量的噪声方差估计法,可以实现噪声协方差矩阵的估计和状态估计误差的解耦,从而使滤波器结果更加稳定。李正等[7]在此基础上,进一步对其进行完善,并将其应用到GNSS/SINS组合导航中,提高了导航系统的精度和稳定性。针对状态模型存在较大误差的情况,研究人员提出了渐消滤波[8-9]和自适应滤波[10],它们分别通过渐消因子和自适应因子来调整预测状态的协方差矩阵,从而控制状态模型误差对滤波结果的影响。由于自适应滤波的关键是构建自适应因子,因此研究人员主要在如何获得最佳自适应因子方面做了大量的研究,并提出了多种构建自适应因子的判断统计量,包括状态不符统计量[4]、方差分量比统计量[11]和预测残差统计量[12]。针对观测量中存在异常观测的情况,中国科学院院士杨元喜教授基于抗差M估计的原理提出了抗差Kalman滤波算法[13],通过对观测量构造等价权矩阵,从而降低异常观测对滤波结果的影响。为了实现对模型误差和观测误差的自适应处理,将抗差滤波和自适应滤波有机融合,提出了抗差自适应滤波算法[14]。由于抗差自适应滤波能够同时对模型误差和观测误差进行控制,从而降低它们对滤波结果的影响,其在动态导航定位中得到了广泛的应用和研究[15-18]。在此基础上,发展出了各种抗差自适应滤波的改进版本,例如针对具有不同可靠性的状态参数模型,发展出了分类因子[19]和多因子抗差自适应滤波[20]。尽管如此,抗差自适应滤波需要在某历元时刻观测量和动力学模型只出现一个异常的情况下,才会有较好的效果;当观测量和动力学模型同时出现异常时,会出现抗差自适应滤波同时增大和减小增益矩阵的矛盾。针对该问题,文献[21]提出了分步抗差自适应滤波方法,基于抗差有偏估计方法首先获得状态参数的估值并对观测量进行修正,然后再进行自适应滤波从而消除动力学模型误差对定位结果的影响。分类抗差自适应滤波在精密度要求不高的动态导航定位中具有较好的效果,但由于抗差有偏估计的精度有限,并不适用于精密度较高的PPP/INS组合导航中。
本文分析了常规抗差自适应滤波算法在以PPP为核心的动态精密导航定位应用中存在的问题,并基于分类因子自适应滤波原理提出了一种抗差自适应分步滤波算法。该算法将抗差自适应滤波分为2个滤波阶段执行,可以准确地识别和分离观测粗差和运动异常扰动对定位结果的影响。为验证算法的性能,采用实际的动态测试数据进行模拟测试。测试结果表明,抗差自适应分步滤波算法可以进一步增强滤波算法抵抗观测粗差和运动异常扰动对定位结果的影响,提高PPP/INS组合导航系统的稳定性和可靠性。
1 PPP/INS紧组合数学模型
对于PPP/INS紧组合滤波模型,状态参数向量x取为
x=(δr,δv,δφ,ba,bg,bclk,dclk,Zr,BIF)T
(1)

1.1 紧组合状态方程
将加速度计常值零偏和陀螺仪常值漂移建模为一阶马尔可夫过程,同时将钟漂、对流层延迟和载波相位偏差建模为高斯白噪声过程,各参数的状态模型为
(2)

根据式(1)描述的各参数的状态模型,可构建状态方程的一般形式为
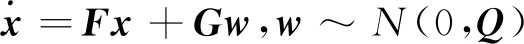
(3)
式中,F为状态转移矩阵;G为过程噪声矩阵;Q为过程噪声协方差矩阵。
1.2 紧组合观测方程
对于PPP/INS紧组合导航,观测量由INS推算的伪距、相位和多普勒与GNSS测量得到的伪距、相位和多普勒分别作差得到,其观测模型分别为
(4)
根据式(3)所述的观测模型,当观测卫星数量为n颗时,可构造观测方程,写成一般形式为
y=Hx+ε,ε~N(0,R)
(5)
式中,R为观测噪声协方差矩阵;观测向量y和观测矩阵H分别为
(6)
(7)

2 抗差自适应滤波算法
2.1 常规抗差自适应滤波
观测粗差和运动模型异常是影响动态导航定位性能的主要因素,为控制观测粗差和状态预测信息异常对状态参数估值的影响,通常采用抗差自适应滤波对参数进行估计。状态参数的估值可表示为
(8)
(9)

对于自适应因子的构造,文献[4,11,12]给出了三种构造自适应因子的判别统计量,包括状态不符值统计量、方差分量比统计量和预测残差统计量。为避免观测信息不可靠时对自适应因子构造的影响,通常采用状态不符值统计量
(10)
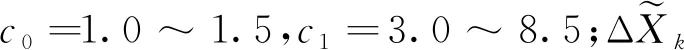
(11)
当观测量中含有粗差时,可通过式(12)构建等价权矩阵来降低含有粗差观测量的权重,即
(12)
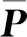
(13)
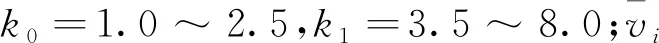
从式(9)可以看出,通过调节等价权矩阵和自适应因子ak都能改变增益矩阵,从而实现对观测粗差和预测状态异常的控制。然而,增大等价权矩阵或减小自适应因子ak都会引起增益矩阵的增大,因此当观测量和预测状态信息均含有异常时,如果不能正确地分离观测异常和预测状态信息异常对滤波结果的影响,可能会导致对异常信息的误判,从而得到不真实的等价权矩阵和自适应因子ak,最终导致参数估值向量无法收敛到正确的极值点。此外,采用状态不符值统计量对运动模型异常进行诊断时,为获得可靠的诊断结果,由式(11)确定的状态参数最小二乘抗差解应尽可能准确。然而,在PPP中,最小二乘抗差解忽略了模糊度参数稳定的特性,使基于单历元观测信息求得的状态参数解精度较差,容易对运动模型异常产生误判。此外,通过式(13)构建观测量的等价权矩阵时,由于标准化残差统计量耦合了预测状态误差,当运动模型存在异常时,会发生对观测异常的误判。综上分析,抗差自适应滤波算法在PPP/INS组合导航系统的实际应用中,需要解决以下2个问题。
1)采用最小二乘抗差解构造的状态不符统计量由于精度有限,会对运动模型异常产生误判。当运动模型出现异常时,由于标准化残差检验统计量耦合了预测状态误差,会将运动模型异常误判为观测异常。因此,需要对观测异常和运动模型异常进行准确的识别。
2)当观测异常和运动模型异常同时存在时,为消除观测异常需要减小增益矩阵,为消除运动模型异常需要增大增益矩阵,导致二者是矛盾的。因此,需要正确分离观测异常和运动模型异常对定位结果的影响。
2.2 抗差自适应分步滤波
式(1)中所描述的各状态参数,由于对流层延迟参数、不发生周跳时的模糊度参数、加速度计和陀螺仪的常值零偏通常是比较稳定的,采用随机游走过程可以较为准确地描述其动态模型;而对于位置、速度、姿态角、钟差和钟飘状态参数,由于受各种因素的影响难以构建准确地动态模型。因此,根据各状态参数动态模型的准确性可以将状态参数分为两类,即
(14)
式中,x1为第一类动态模型不准确的状态参数,包括位置、速度、姿态、钟差和发生周跳时的模糊度参数;x2为第二类动态模型准确已知的状态参数,包括对流层延迟、不发生周跳的模糊度参数、陀螺仪常值漂移和加速度计常值零偏。
对上述两类状态参数分别构建自适应因子
(15)
式中,ax1和ax2分别为第一类和第二类状态参数的自适应因子。根据分类因子自适应滤波原理[19],状态参数的自适应滤波解可表示为
(16)
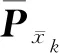
(17)
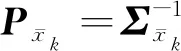
根据分类因子自适应滤波[19]的原理可知,对某一类状态参数的自适应因子进行调节,则仅改变该类状态的预测信息对状态参数估值的贡献程度;当自适应因子设置为ax1=0时,表示该类状态参数的预测信息将不对状态参数的估值产生影响;当自适应因子设置为ax1=1时,则表示不改变状态预测信息对状态参数估值的影响。在PPP/INS组合导航定位中,由于第二类状态参数的状态模型是准确已知的,因此不需要对其进行调节,并将其自适应因子取为ax2=0,而仅对第一类状态参数的自适应因子ax1进行调节。基于上述分析,本文提出了一种定位抗差自适应分步滤波算法,其流程如图1所示。
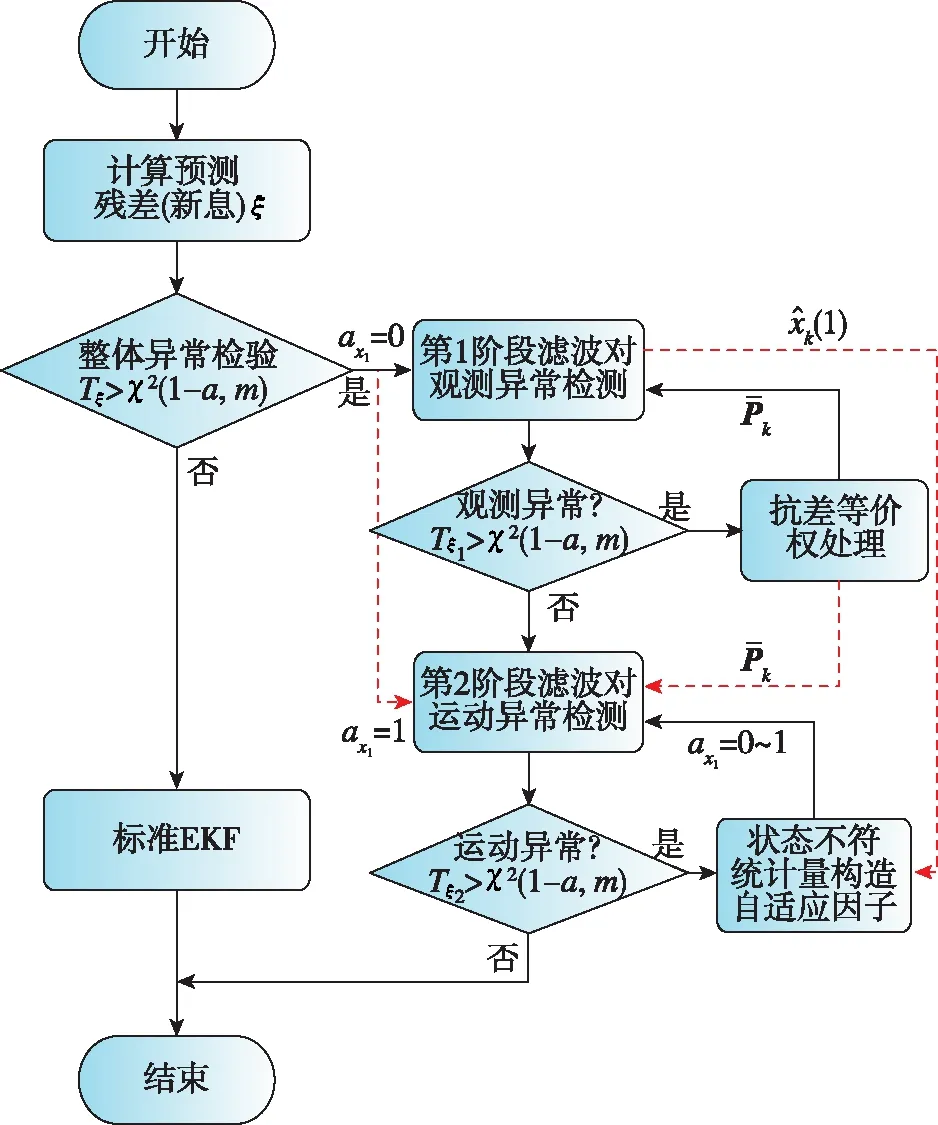
图1 PPP/INS抗差自适应分步滤波算法流程Fig.1 Flow chart of two-step robust adaptive filtering algorithm
从图1中可知,PPP/INS抗差自适应分步滤波算法可概括为以下3个步骤。
步骤1:基于预测残差ξ对观测异常和运动异常进行整体检验,检验统计量构造为
(18)
式中,χ2表示卡方检验;m为观测量个数;Qξ为预测残差协方差矩阵。给定显著性检验水平a,如果Tξ>χ2(1-a,m),则执行抗差自适应分步滤波算法,对观测异常和运动异常分步进行检测和处理。
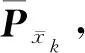
(19)
根据预测残差与观测残差和预测状态误差之间的关系,式(19)可改写为
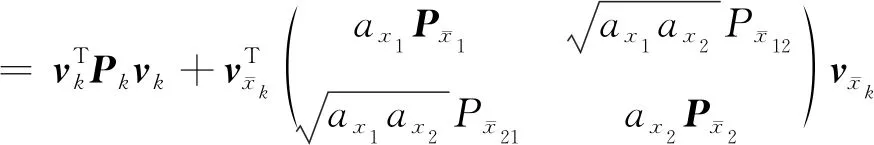
(20)
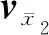
(21)
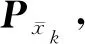
(22)
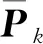
(23)
并基于三段权函数式(10)获取第一类状态参数的自适应因子ax1。根据式(17)重新计算预测状态向量的等价权矩阵,并根据式(21)获取第2阶段滤波的状态参数估值作为最终输出。
综上所示,抗差自适应分步滤波算法在执行第1阶段滤波时,将模型不准确的第一类状态参数对应的自适应因子设置为ax1=0,从而降低了运动模型的预测信息对定位结果的贡献,此时基于新息的卡方检验统计量将主要反映观测异常;在执行第2阶段滤波时,将自适应因子重置为ax1=1,由于第1阶段滤波已经对观测异常进行了处理,此时基于新息的检验统计量将主要反映运动异常。因此,本文提出的抗差自适应分步滤波算法可实现对观测异常和状态预测信息异常的有效识别和分离。
3 实验测试与分析
为测试抗差自适应分步滤波算法在PPP/INS组合导航系统中实际应用的性能,采用NovAtel公司的SPAN GNSS/INS组合导航设备于2018年6月30日在北京航空航天大学体育场采集了一组时长约20min的小推车动态测试数据,该测试数据卫星观测质量较好。实验设备及安装示意图如图2所示,该组合导航设备所搭载的惯性测量单元(Iner-tial Measurement Unit,IMU)传感器精度为战术级,采样频率为125Hz,其性能指标如表1所示。

图2 实验设备及安装示意图Fig.2 Experimental equipment and installation diagram

表1 SPAN PwrPak7-E1设备IMU (G320N) 性能参数
对采集的测试数据作如下处理:在300~310历元时刻,在伪距和相位观测量中分别随机加入1m和20m的粗差模拟观测异常;在700~710历元时刻,在惯性传感器采集的加速度数据中加入0.5m/s2的加速度误差模拟运动异常扰动;在1000~1010历元时刻,同时引入观测粗差和运动异常扰动。采用以下三种滤波方案分别进行定位解算:
方案1:扩展Kalman滤波(Extended Kalman Filter, EKF);
方案2:常规抗差自适应滤波(Robust Adaptive Kalman Filter, RAKF);
方案3:抗差自适应分步滤波(RA2KF)。
采用上述三种方案对PPP/INS组合导航进行滤波解算,其中方案2和方案3中观测粗差和运动异常扰动的检验阈值均设置为k0=1.3、k1=3.5、c0=1.5和c1=5.0。各方案解算的位置、速度和姿态误差的时间序列如图3~图5所示,其统计结果如表2所示。由方案3算法计算得到的各历元时刻的自适应因子如图6所示,其对观测异常和运动异常的检测结果如图7所示,图中T1和T2分别为观测异常和运动模型异常检验统计量。
从图3、图4、图5和表2中可以看出,在3处观测量中含有粗差和运动模型存在异常扰动的历元时刻,方案1获得的位置、速度和姿态导航参数均出现了较大的偏差,其位置和速度误差在3个方向(东,北,天)上的统计结果分别为(14.7cm,8.9cm,40.5cm)和(4.7cm/s,7.8cm/s,22.2cm/s),航向、横滚和俯仰角误差分别为18.44°、0.73°和1.399°;方案2获得的位置和速度误差在3个方向(东,北,天)上的统计结果分别为(13.7cm,7.4cm,34cm)和(4.2cm/s,5.7cm/s,6.6cm/s),航向、横滚和俯仰角误差分别为10.19°、0.424°和0.735°。方案2比方案1在3个方向(东,北,天)上的定位精度和速度精度分别提高了(1.0cm,1.6cm,6.5cm)和(0.5cm/s,2.1cm/s,15.6cm/s),航向、横滚和俯仰角精度分别提高了8.25°、0.30°和0.66°。方案2获得导航定位参数的精度和稳定性均比方案1有所改善,但在700~710历元和1000~1010历元时刻仍出现小幅波动,这是由于常规抗差自适应滤波算法未能准确识别和分离观测粗差和运动异常扰动。方案3获得的位置和速度误差在3个方向(东,北,天)上的统计结果分别为(13.2cm,7.0cm,33.7cm)和(4.0cm/s,4.5cm/s,4.6cm/s),航向、横滚和俯仰角误差分别为9.901°、0.25°和0.674°。方案3比方案2在3个方向(东,北,天)上的定位精度和速度精度分别提高了(0.5cm,0.3cm,0.3cm)和(0.2cm/s,1.2cm/s,2.0cm/s),航向、横滚和俯仰角精度分别提高了0.289°、0.174°和0.06°。方案3的解算结果与方案2相比,其精度和稳定性得到进一步改善,这是因为方案3对观测粗差和运动异常扰动进行了正确识别和分离。从图6和图7中可以看出,抗差自适应分步滤波算法准确地检测出了3处观测异常和运动异常扰动,在运动模型存在异常扰动的历元时刻,抗差自适应分步滤波算法通过调节自适应因子来降低运动异常对定位结果的影响。
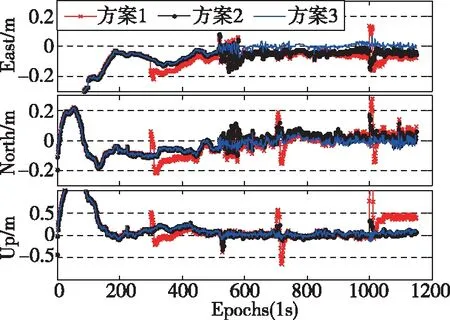
图3 三种滤波方案下PPP/INS组合导航位置误差Fig.3 Position errors of PPP/INS under the three filtering schemes
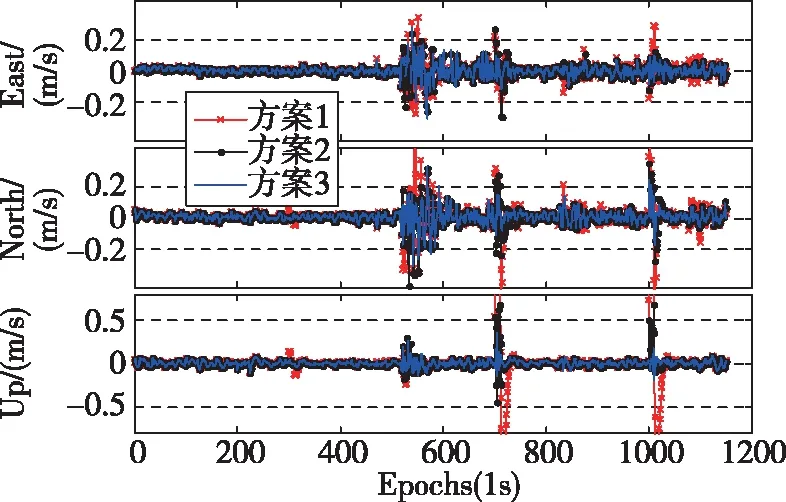
图4 三种滤波方案下PPP/INS组合导航速度误差Fig.4 Velocity errors of PPP/INS under the three filtering schemes
图5 三种滤波方案下PPP/INS组合导航姿态误差Fig.5 Attitude errors of PPP/INS under the three filtering schemes
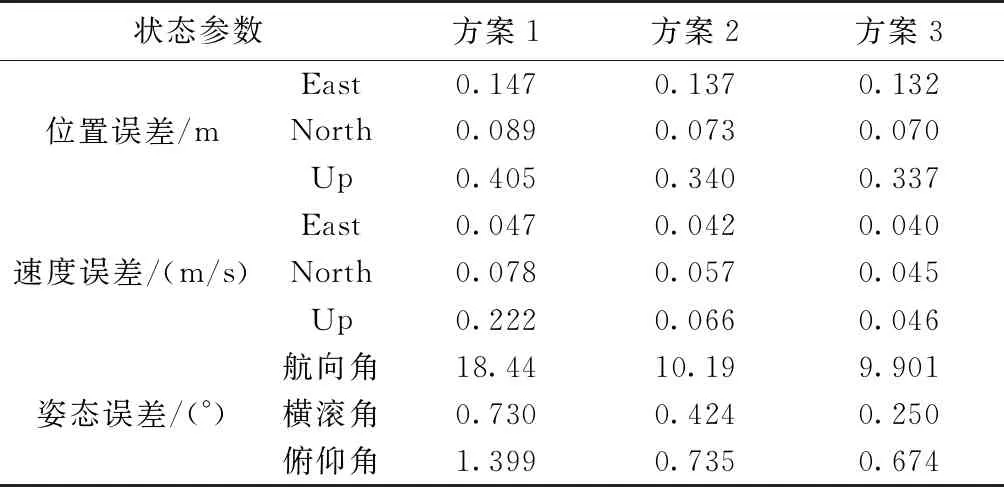
表2 位置、速度和姿态误差的RMS统计结果
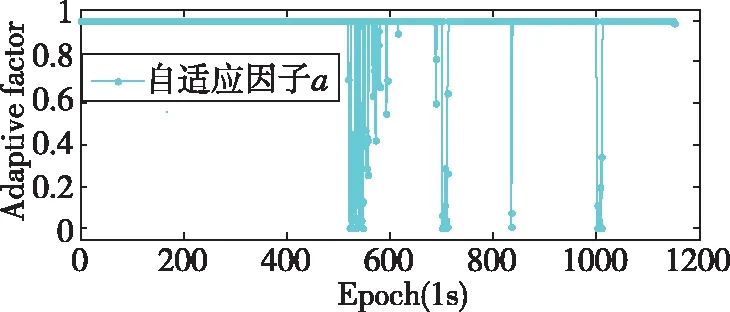
图6 RA2KF滤波方案各历元时刻的自适应因子aFig.6 Adaptive factors calculated by RA2KF
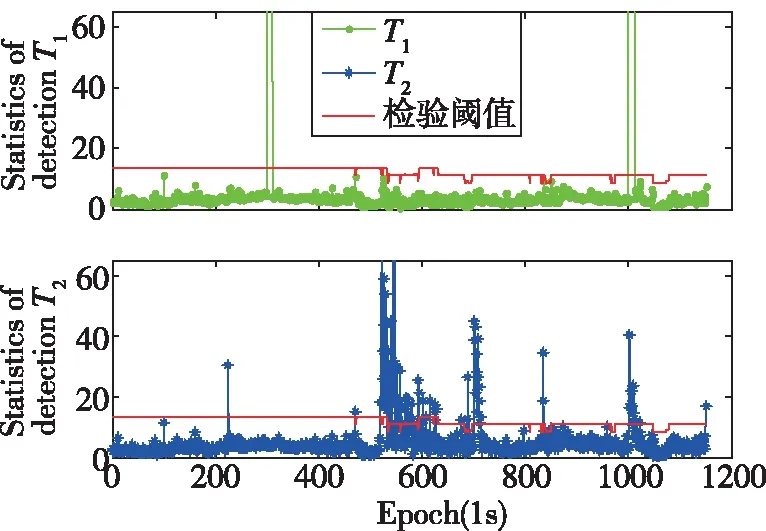
图7 RA2KF滤波方案对观测异常和运动异常的检验结果Fig.7 Detection results of observation gross errors and kinematic abnormality by RA2KF
综上所述,采用抗差自适应分步滤波算法可以有效增强PPP/INS组合导航系统的性能,提高组合导航系统的鲁棒性和稳定性。
4 结论
本文针对常规抗差自适应滤波算法存在难以准确识别和分离观测粗差及运动异常扰动对定位结果影响的问题,基于对PPP/INS组合导航状态参数特征的分析,并借鉴分类因子自适应滤波原理,提出了一种抗差自适应分步滤波算法。算法分析与实验结果表明:
1)抗差自适应滤波将抗差与自适应分为2个滤波阶段执行,实现了对观测粗差和运动异常扰动的准确识别和分离。因此具有比常规抗差自适应滤波算法更优的定位性能,可以显著地增强滤波算法抵抗观测粗差和运动异常扰动对定位结果的影响,提高PPP/INS组合导航定位结果的稳定性和可靠性。
2)本文提出的抗差自适应分步滤波算法主要针对状态参数模型具有不同精度的一些应用对象,而对于状态模型都不准确的应用对象需要进一步研究。
