一类时间不一致问题均衡控制的存在性

张 婷， 彭云飞， 张大永

（贵州大学数学与统计学院，贵州贵阳550025）

1 问题及主要结果

首先建立数学模型.让Rn表示n维实欧氏空间，U∈Rm是非空有界闭凸集.本文的控制集为U［t，T］＝｛u：［t，T］→U｜u 可测，t∈［0，T）｝，受控系统为常微分方程

目标泛函为

模型中的受控系统是基于确定型投资组合模型提炼所得，性能指标是双曲贴现和期望方差组合的特例，更一般地是相应的随机模型.本文的问题是极小化目标泛函，即问题（P）：寻求一个反馈控制¯u，使得对任意的 ε ＞0，v∈U 和任意的（t，x）∈［0，T］×Rn有

其中

如果问题（P）有解¯u，则称¯u为均衡控制.

上述问题与经典最优控制问题有着本质区别，主要是最优控制问题的目标泛函不依赖于初始状态，只优化一个目标泛函，最优策略具有一致性（符合动态规划原理），通常将具有此特征的问题称为时间一致问题.经典最优控制问题之所以有一致性，是因为假设了决策者在做决策时不受决策者的心态以及外界环境变化等因素的影响.这一假设虽然对许多工业问题是合理的，但遇到金融等复杂领域时，此假设往往由于过于理想化而导致问题失真.为此，不得不考虑环境变化以及决策者的心态等因素对决策的影响，体现在数学模型上就是目标泛函始终依赖于初始状态.因此，需要优化一族性能指标（无穷不可数多个），而非一个，这导致所谓最佳策略不具有一致性（不满足动态规划原理），这样的问题常被称为时间不一致问题.关于此问题的研究，至少可追溯到 1739年 Hume［1］和 1759年Smith［2］所做的工作.特别是 1955 年 Strotz［3］进行数学公式化后，引起许多学者兴趣，相关工作可参考文献［4-11］.特别地，Yong［9］在 2012 年将时间不一致问题视为时间一致问题的极限，从非合作博弈的角度出发，研究时间不一致问题，获得开环形式的均衡控制.2017年Yong［7］进一步研究了时间不一致随机LQ控制问题，深入研究了开环闭环均衡策略.

本文虽然也将时间不一致问题视为时间一致问题的极限，但构造时间一致问题系列的方法完全不同于雍炯敏教授的构造方法（分割时间区间）.其次，雍教授主要获得了开环形式的均衡控制.虽然也考虑了闭环形式的解，但与本文闭环形式解的定义有本质的不同（可参阅文献［7］）.经济学家大多认为，只有闭环控制才能刻画时间不一致问题的特征，即闭环控制能够吸纳环境以及决策者心态变化等因素对决策的影响，而开环控制不具备这个特征.本文的闭环形式的均衡控制是许多经济学家希望引入的.

在陈述主要结果之前，首先引进一些基本假设.

［F］映射 f：［0，T）× Rn→Rn关于时间变量 t可测，且存在常数L＞0使得对任意的xi∈Rn（i＝1，2），t∈［0，T）有

［G］映射 g：［0，T）× Rn× ［0，T）×Rn→R 关于时间变量t可测，且存在常数L＞0使得对任意的（ti，xi，yi）∈［0，T）× Rn× Rn（i＝1，2），s∈［0，T）有

［H］对任意的开环控制u（·），都能找到一个闭环的二元可测函数u（·，·）使得

其中x（·）是受控系统对应的解.

虽然假设［H］中等式两端的同一符号表示的内涵不一致，但在本文不至于引起混淆的情况下，为了简洁，用同一符号表示（其它地方同此）.此外，假设［F］和［G］是通常的假设，即使是时间一致问题解的存在性也是需要的.对于假设［H］，类似于Filippov选择性定理，在适当的条件下，此假设是可验证的.在本文中，由于篇幅限制，在此不再证明.

在上述假设下，有如下的主要结论.

定理 A若假设［F］、［G］和［H］成立，则问题（P）至少有一反馈均衡控制.

2 定理A的证明

引理1若假设［F］成立，则下列结论成立：

和

证明根据假设［F］有

结合Gronwall不等式，可知（5）式成立.而且，

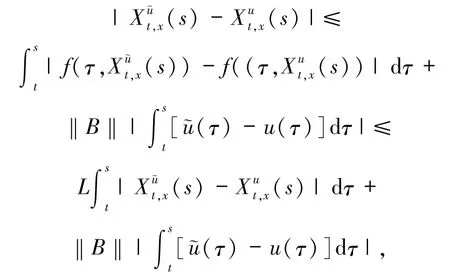
由此可断言（6）式成立.

引进问题（P1）：寻找控制 u1∈U［0，T］使得

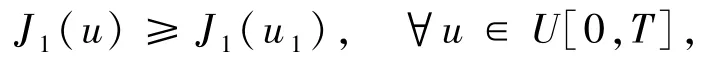
其中

对问题（P1），不难证明下面的存在性结论.

引理 2若假设［F］和［G］成立，则问题（P1）至少存在一个最优闭环控制u1.

引进偏微分算子Av为

不难证明下面的偏微分方程

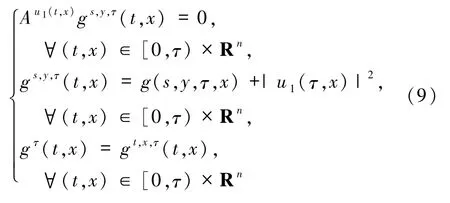
有唯一解

其中（s，y）∈［0，T）×Rn.令

问题（P2）：寻找控制函数 u2∈U［0，T］使得

类似地，对问题（P2），也有如下存在性结论.

引理 3若假设［F］和［G］成立，则问题（P2）至少存在一个最优闭环控制u2.

继续上述过程，构造控制函数列｛uk｝k≥1、.

根据关于控制策略集的假设，存在｛uk｝k≥1的子列（不妨设为其自身）在L2［0，T］中弱收敛到某个¯.结合假设［H］，存在闭环控制¯u使得

根据 Ascoli-Arzela定理和引理 1，不难证明在 C［0，T］中是紧的并且

进而可推断函数列

其中

是Rn中的有界闭集，且

其中（t，x）∈［0，τ）×E.进而能够证明

及

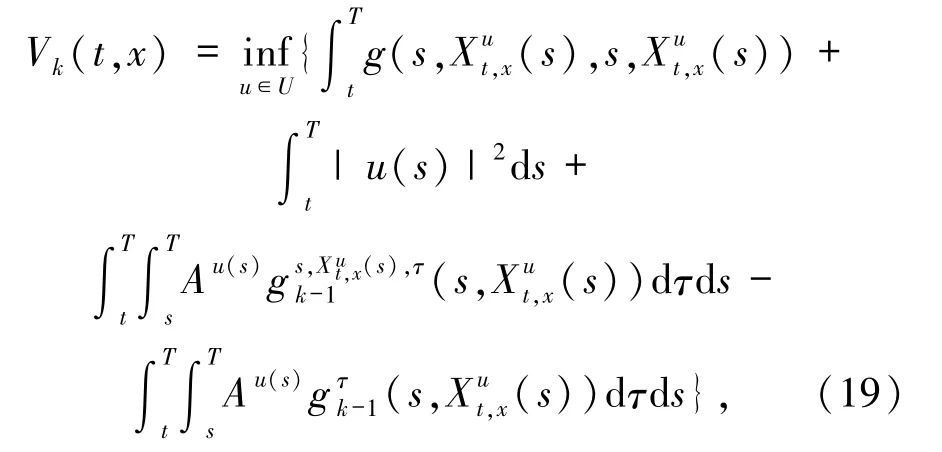
于是下列HJB方程

有粘性解 Vk.进而，结合（12）～（14）和（16）～（17）式，可推断下列的HJB方程

有粘性解V并且适合

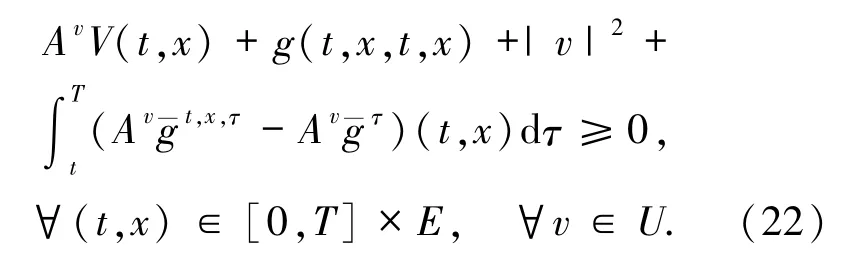
结合（23）式有

结合（22）式可得

对任意的（t，x，v）∈［0，T）× E × U，上述结论均成立，因此是问题（P）的一个均衡控制.这就完成了主要结果的证明.

3 结束语

时间不一致控制问题是数学与金融交叉的前沿课题，其研究一直方兴未艾.但一直未取得理论上的突破，未能像最优控制理论那样有完善的求解方案.本文对一类常微分系统支配的时间不一致控制问题进行讨论，提出了一个求解方案，特别是解的定义不仅符合数学要求，更是经济学家希望的.不仅如此，本文所给的方案，对建立时间不一致控制问题的一般理论也是有益的.

致谢贵州省科技计划项目（黔科合平台人才［2017］5788号）对本文给予了资助，谨致谢意.