延迟索赔风险模型的最优再保险

肖鸿民， 王占魁， 刘月娣

（西北师范大学数学与统计学院，甘肃兰州730070）

近年来，在对经典模型的各种改进中，延迟风险模型是更贴近保险实际的一类风险模型，也是保险公司在索赔过程中常常会遇到的一种情况：在主索赔发生后的某个不定时间，还会由此引起附加索赔，即延迟索赔.例如：当一起车祸发生后，担保人不仅要赔付车的损失，如买了第三方保险，担保者在一段时间后还要为第三方赔付.针对这类情况，Waters等［1］提出了带延迟索赔的风险模型.国内外许多学者对此产生了浓厚的兴趣.Yuen等［2］运用鞅的方法研究了延迟风险模型的最终破产概率；Xie等［3］讨论了随机利率下延迟索赔风险模型总股息的期望贴现；最近，肖鸿民等［4］又研究了相依赔付带投资的延迟风险模型的极限性质.

而在现实生活中，意外巨灾频繁发生所引起的巨大索赔使保险公司损失严重，而再保险是防范和化解巨额风险的重要手段.因此，关于再保险的研究逐渐得到保险公司的重视，对再保险的理论操作也日益增多.而再保险中最关键的问题是最优再保险，即考虑以何种形式分保及具体分保的额度.为此，保险人需要在风险与收益之间进行平衡并尽可能做出最为合理的决策.实际上，最优再保险也一直是精算学主要的研究内容之一.Schmidli［5］研究了最优比例再保险问题；Hipp等［6］研究了非比例再保险控制问题；Cao等［7］研究了破产概率最小的最优再保险与最优投资问题；张茂军等［8］研究了再保险与有限时间破产概率问题；Yang等［9］假定风险资产价格满足跳扩散模型，考虑了最终财富效用最大化的最优投资问题；林祥等［10］在 Yang等［9］模型的基础上假定保险公司还可以投资再保险业务，研究了在风险资产价格满足跳扩散模型下保险公司的最优投资和最优再保险策略；Centeno［11］在最大化期望指数效用和调节系数的优化标准下研究了相依双险种模型超额赔款再保险的最优自留限额；Bai等［12］通过扩散逼近，在期望值保费原则下研究了最小破产概率的最优再保险形式及其自留额；Liang等［13］则在方差保费原则和最大化终期财富期望指数效用的优化准则下，分别研究了跳跃模型和扩散逼近模型的最优比例再保险；Yuen等［14］采用相同的优化准则，但将相依双险种模型推广到更贴近实际的相依多险种模型，并采用期望值分保费原则分别给出了跳跃模型和扩散逼近情形下的最优结果；最近，张节松等［15］研究了方差分保费原则下相依多险种模型的最优再保险.

本文将文献［15］中方差分保费的思想应用到延迟索赔风险模型中，以最小化破产概率为优化准则，当索赔次数是齐次Poisson过程时，通过扩散逼近并运用动态规划原理，得到了最优的自留风险水平及最小破产概率的显式表达式.结合数值模拟很好的验证了本文的结论，这对保险公司分散风险和财务稳定有重要的参考价值.

1 模型假设与扩散逼近

对于延迟索赔模型，Ut表示保险公司在t时刻的盈余过程：

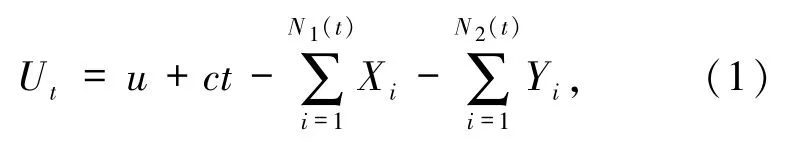
其中，

（i）u为初始资金，c为单位时间收取的保费.

（ii）Xi为第i次主索赔的索赔额，Si是发生第i次主索赔的时刻.

（iii）Yi为延迟索赔额.Ti为延迟赔付间隔.

为了刻画索赔之间的相依性，设遵循的相依结构为

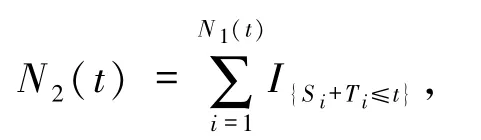
据此，盈余过程Ut可表示为

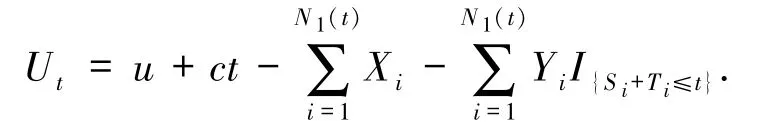
对于本文的研究，作如下基本假设.

1）主索赔序列｛Xi，i＝1，2，…｝独立同分布于X，它们的共同分布为F，其一阶矩和二阶矩存在，分别记延迟索赔序列｛Yi，i＝1，2，…｝独立同分布于Y，它们的共同分布为G，其一阶矩和二阶矩存在，分别记.

2）延迟赔付间隔｛Ti，i＝1，2，…｝独立同分布于T，它们的共同分布为H.

3）索赔额X和Y相互独立.计数过程N1（t）是强度为λ的齐次Poisson过程并且

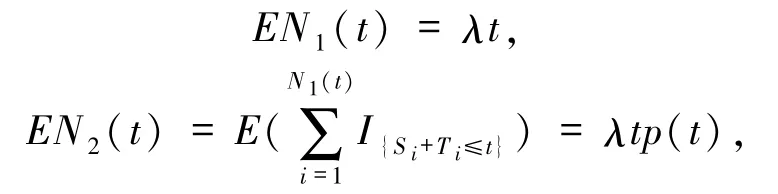
其中，p（t）＝p ｛U ＋T≤t｝，U 为（0，1）上的均匀分布.

为了保障巨额损失，保险公司安排了t时刻自留风险水平为ft的再保险策略.对于ft，约定0≤ft（x）≤x，且在（0，∞）上单调递增.假设分保费按照方差分保费原则计算，安全负载为θ＞0，记M＝X-ft（X），N＝Y-ft（Y）.则

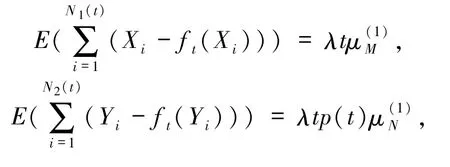
假定π为所有的可行策略，则原保险公司t时刻的净保费收入率为

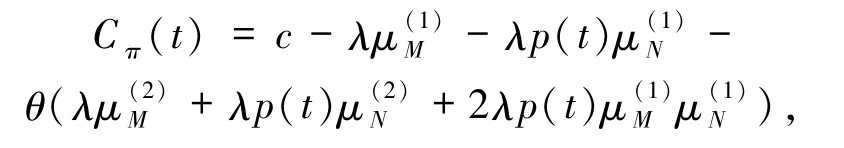
于是，原保险公司的盈余过程为

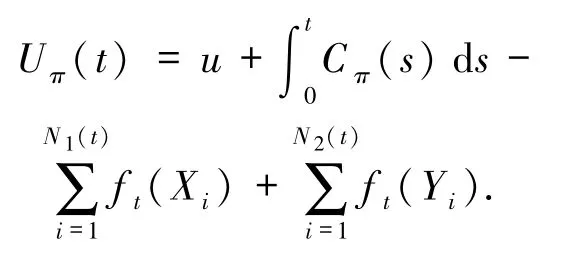
针对延迟索赔风险模型，一般要获得破产概率最小时的最优再保险策略的显式解是很困难的，为使问题可处理并获得显式解，采用扩散逼近的形式.为此，先给出经典风险模型的扩散逼近结果.

引理 1［16］设｛ζi，i≥1｝独立同分布，ζ的一阶矩和二阶矩存在，N（t）服从强度为γ的Poisson分布，则复合Poisson过程可扩散逼近为其中 B（t）表示标准 Brown 运动.

由引理1知，在再保险策略π的安排下，盈余过程Uπ（t）可扩散逼近为

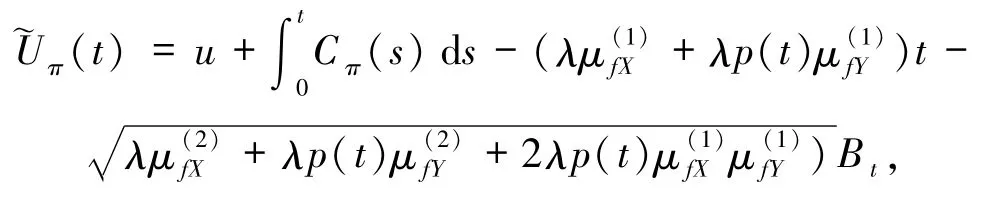
其中

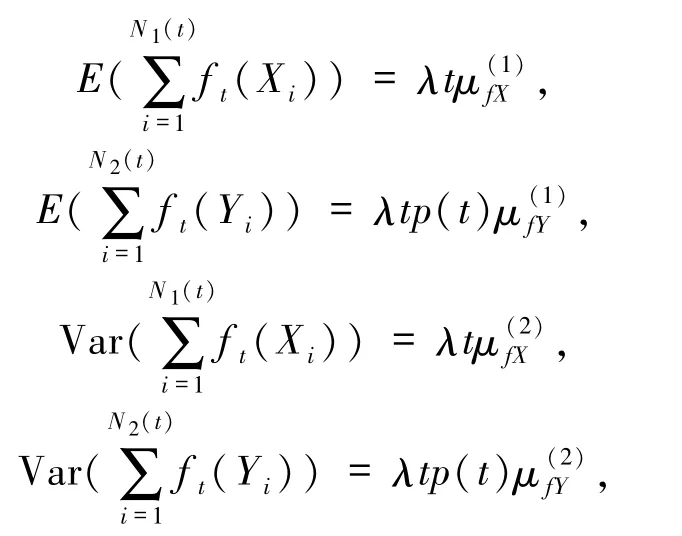
Bt为标准Brown运动.不妨记

为索赔计数过程之间的相关性强度.则盈余过程变为

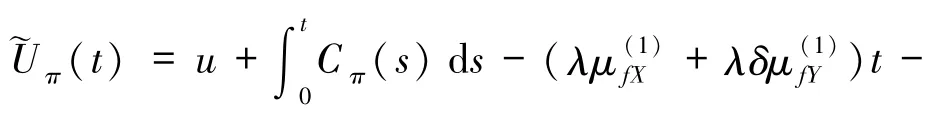
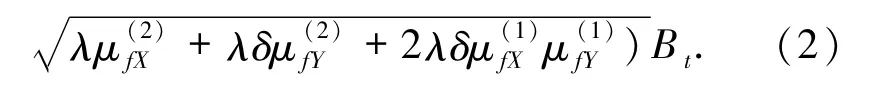
2 最优再保险策略

（2）式的扩散逼近为研究最优再保险决策问题并获得显式解奠定了基础.下面假定保险人为应付巨额的损失，在t时刻安排了自留风险比例为q（t）的再保险业务，0≤q（t）≤1，令 ft（x）＝q（t）x.由于采用的是方差分保费原则，根据Hipp等［6］命题7，此时的最优再保险形式为比例再保险.在再保险策略 q（t）下，盈余过程（t）满足随机微分方程

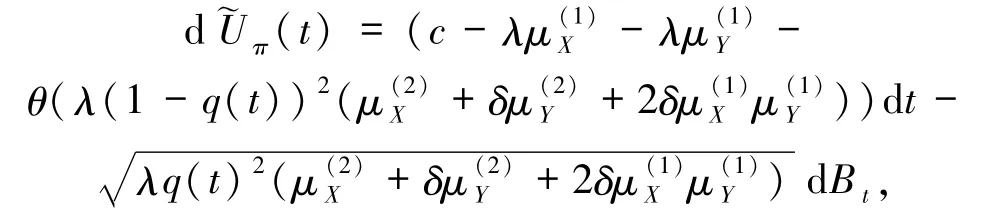
即破产概率达到最小，记为ψ（u）.

为解决优化问题，采用动态规划方法［17］和HJB方程，通过标准论证可知，如果最优值函数ψ（u）二阶连续可微，则 ψ（u）必然满足下面 HJB方程

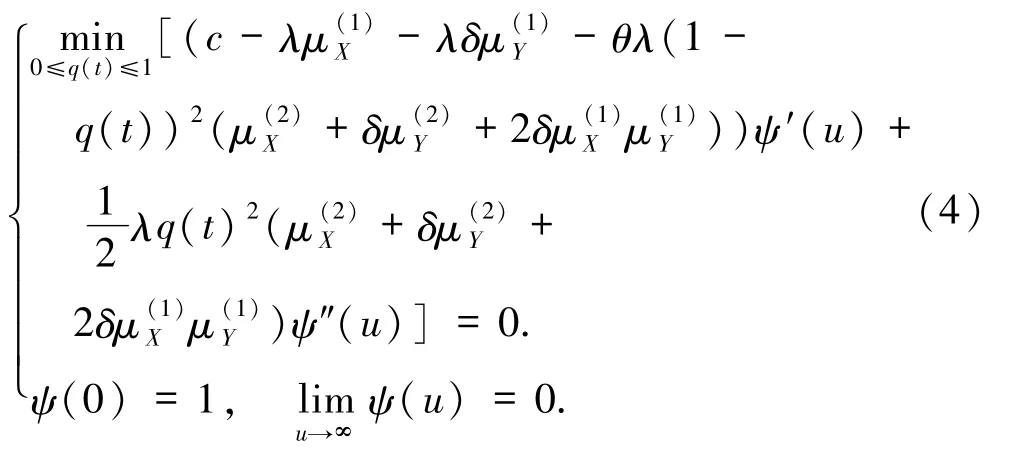
根据文献［18］的识别定理，说明由HJB方程（4）的二次连续可微解即可得到优化问题（3）的唯一解.下面是本文的主要结果.

定理1设v（u）为上述HJB方程（4）的解且二次连续可微，则 ψ（u）即为 v（u），并且如果对所有的u＞0有

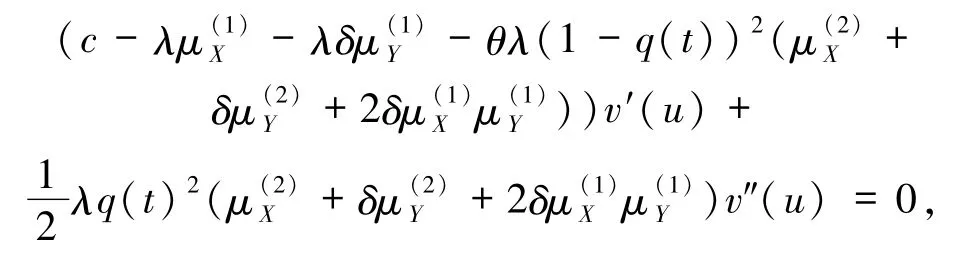
则π*＝q*（t）∈Π 最优，使得

下面寻求 HJB方程（4）的二次连续可微解v（u），也就得到了最优值函数 ψ（u），假定 v（u）为二次连续可微的凸函数，且满足v″（u）＞0，根据最优解π*应满足HJB方程（4）第一式且为唯一解.令

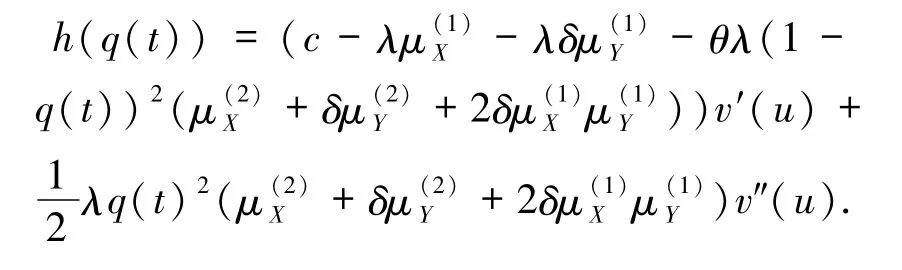
对 h（q（t））关于 q（t）求导且令 h′（q（t））＝0，得到

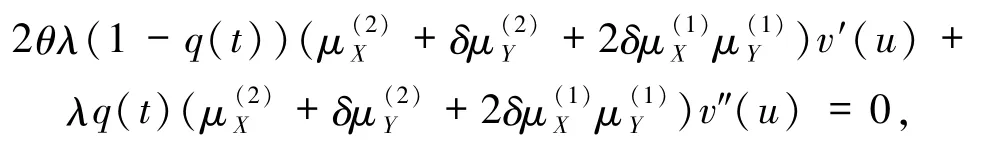
解得

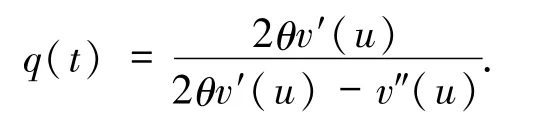
又因为 0≤q（t）≤1，则 q（t）为极小值点，此时 q（t）必为最小值点，即

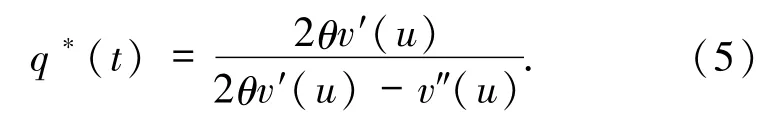
将（5）式代入 h（q*（t））＝0，得到

下面求解最优值函数.由（5）式可得

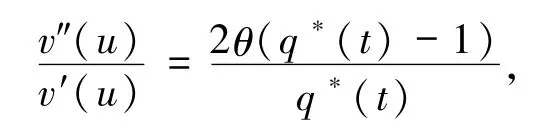
根据微分方程求解得

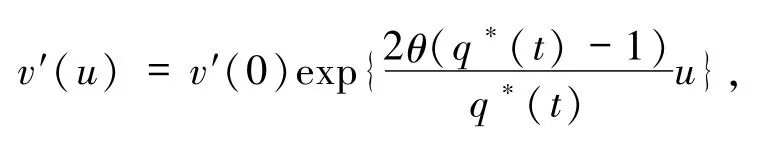
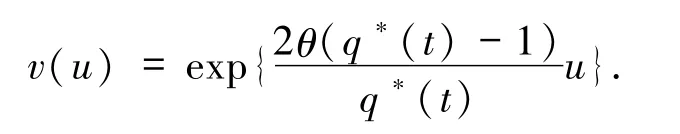
易见v（u）为二次连续可微的凸函数且满足v″（u）＞0，于是可知 ψ（u）＝v（u）.

综上所述，可得优化问题（3）的最优解及对应的值函数.以定理的形式给出.

定理2优化问题（3）的最优值函数为

最优策略为π*＝q*（t），其中 q*（t）由（6）式确定.

注定理2是在最小化破产概率的优化准则下得到的，从显式表达式可以看出，最优策略和最小破产概率不仅与安全负载、保费的收入率和索赔分布有关，还与计数过程之间的相关性强度密切相关.本论文的结论对实际的保险公司具有一定的参考价值，但选用不同的优化准则以及不同的风险模型，获得更为有效的HJB方程求解手段将是本文进一步要做的研究工作.

3 数值模拟

下面给出Matlab数值结果，并分析了初始资金u对破产概率的影响以及随着u的动态变化对（7）和（8）式进行了对比.根据文献［19］，当索赔分布为指数分布时延迟索赔风险模型（1）的破产概率φ（u）的显式表达式如下：

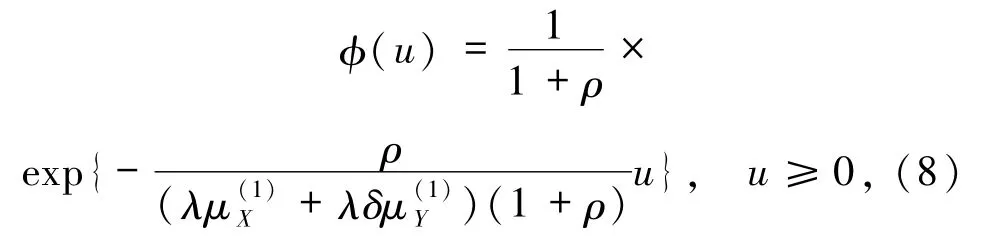
其中，ρ为安全负载.

首先给相应参数赋值.假定主索赔额服从参数为1的指数分布，延迟索赔额服从参数为2的指数分布.并假定保险公司的保费收入率c＝2.3，再保险费按照方差原则计算，安全负载为θ＝0.2.相关性强度δ＝0.2.计数过程满足参数为λ＝2的齐次Possion过程.固定以上参数，得到了破产概率随初始资金变化的数值模拟值如下表.

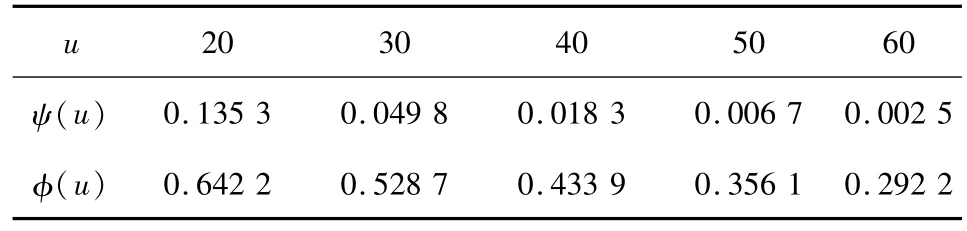
表1 破产概率随初始资金变化的模拟值Tab.1 Simulated values of ruin probability with initial capital

从表中的数值结果可见，破产概率 ψ（u）、φ（u）均表现出随u的增加而减小的趋势，这与上述定理的理论性质以及保险风险理论中破产概率关于初始资金单调递减的性质相符合.从保险公司的实际情况考虑，当初始资本u较小时，保险公司的破产概率较大，并且从表中可以看出安排再保险时的破产概率 ψ（u）比无再保险时的破产概率φ（u）要小的多.由此可见，当初始资本u较小时，为了使保险公司可持续发展，安排再保险策略是非常有必要的，这为保险公司分散风险和财务稳定提供一些启示性参考.