Cardinal Invariants of Ideals on Uncountable Groups

ZHU Huiling， ZHENG Fudan

（1.School of Data and Computer Science，Sun Yat-sen University，Guangzhou 510006，Guangdong；2.Three Gorges Mathematical Research Center，Three Gorges University，Yichang 443002，Hubei；3.Guangzhou College，South China University of Technology，Guangzhou 510800，Guangdong）

Abstract：In this paper，we investigate the cardinal invariants on ideals of an uncountable Abelian groups.We find connections among these cardinal invariants within axiomatic system of set theory.Among others，we prove that if an ideal is weakly uniform，then the strong covering number is no more than the cofinality.We determine all the cardinal invariants for the countable ideal of the real line.

Keywords：cardinal invariants；additivity；uniformity；covering；cofinality

1 Introduction

Application of logic method to algebra has a long history.Most notably， Hrushovski［1］solved the Mordell-Lang conjecture by geometric model theory.Set theorists also tried to extract the power of infinity to algebraic objects，such as groups.Shelah's solution to Whitehead's problem［2］applied the method of forcing （or forcing axioms）；Brendle［3］considered cardinal invariants defined with subgroups；cardinal invariants on ideals of groups had been studied in［4］；［5］considered cardinal invariants about the nowhere dense ideal，etc.

In the present work，we extend the work in ［4］，by proving new theorems，simplifying proofs of old theorems and presenting a concrete example.We also list some interesting questions for future study.Our aim is to draw a more complete picture on this topic.Our notations follow the standard textbooks，such as ［6-8］.

2 preliminary

In this section，we introduce the terminology used in the whole article.The reader are encouraged to find out the basics of set theory in ［9-11］.

Definition 2.1Suppose that G is a set.I is an ideal on G if I⊆P（G）and

1）if A∈I and B⊆A，then B ∈I.

2）if A，B∈I，then A∪B ∈I.

The following are examples of an ideal on G：∅，P（G），I＝P（A）for any A⊆G；［G］＜ω，the collection of finite subsets of G；［G］≤ω，the collection of countable subsets of G.

To avoid the first three examples，we define：

Definition 2.2An ideal I⊆P（G）is nontrivial，if G∉I and ∀g ∈G，｛g｝∈I.

2.1 Cardinal invariants as norms of relationsA cardinal invariant is usually the least cardinality of a set with a given property.Many cardinal invariants can be defined as the norms of relations.See ［12-13］for more details.

R is a relation between two sets S and T if R⊆S×T.In some context，S is called the set of“challenge”while T is the set of“response”.We denote this by a triple （S，T，R）.To avoid triviality，assume that∀a∈S，∃b∈T with（a，b）∈R.In other words，R is a multi-valued function.The dual relation of（S，T，R）is（T，S，﹁ R），assuming which is nontrivial neither.

Definition 2.3The norm of（S，T，R）is

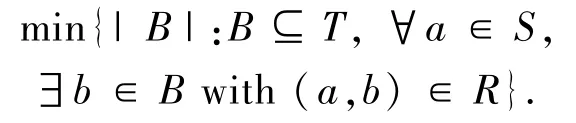
Definition 2.4Let I be a nontrivial ideal on G.We define：

1）the additivity，add（I）is the norm of（I，I，）；

2）the uniformity，non（I）is the norm of（I，G，∉）；

3）the covering number，cov（I）is the norm of（G，I，∈）；

4）the cofinality，cof（I）is the norm of（I，I，⊆）.

We may not mention I unless necessary.Namely，we might write add instead of add（I）.

Clearly，the additivity and the cofinality are cardinal invariants of dual relations.Similar for the uniformity and the covering number.

The following diagram is an easy exercise for the junior reader，where the arrows are interpreted as≤.

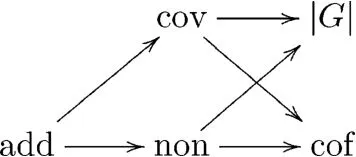
Generally，we can define the following cardinal invariants：

Definition 2.5If S＝T and R is a preorder，then

1）the R-unboundedness is the norm of（S，S，﹁ R）；

2）the R-dominating number is the normof（S，S，R）.

3 Additivity and cofinality related to translation

From now on，we assume that G is an uncountable Abelian group.Notations like ＋，-，0Ghave the obvious meaning.I is a nontrivial ideal on G.Moreover，

1）lisσ-complete：add N1.Namely，if∀n∈ω，An∈I，then；

2）I is invariant under group operations：

（a）∀A∈I，-A＝｛-a：a∈A｝∈I；

（b）∀A∈I，∀g∈G，A＋g＝｛a＋g：a∈A｝∈I.

As examples，let G be the real line，with the usual addition.I could be the ideal of countable sets，the ideal N of null sets or the ideal M of meager sets.

Definition 3.1For A，B⊆G，define that A is a subset of B by translation and denote that A⊆tB if∃g∈G，with A⊆B＋g.

It is easy to observe that⊆tis a preorder.Antisymmetry might fail.For example，Let G＝R，A＝Q and B＝Q＋π.

Definition 3.2We define two cardinal invariants related to translation.

1）coft（I）is the norm of（I，I，⊆t）；

2）addt（I）is the norm of（I，I，⊇t）.

In other words，coft（I）and addt（I）are the dominating number and the unboundedness number on I under the relation⊆t，respectively.Since⊆ is stronger than ⊆t，we have the following：

Fact 3.3add≤addt；coft≤cof.

In many cases of preorders，the dominating number is not less the unboundedness number.Otherwise，there will be one single element which dominates all.In the case of⊆t，it is also true.

Theorem 3.4addt≤coft.

ProofWe give a proof which simplifies the original one.By reductio ad absurdum，let｛B｝be⊆tdominating over I.Since BG，let b∉B.Since｛-b｝∪（-B）∈I，there is some g such that

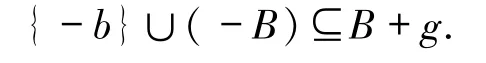
Then we have-b∈B＋g，-b-g∈B，b＋g∈-B⊆B＋g，implying b∈B.This is a contradiction.

Fact 3.5cof≤coft·｜G｜.

In some situation when G＝R and I has a definable feature，there is a dominating family consists of Borel sets.Then coft≤cof≤｜G｜.

4 Strong additivity and covering property

In this section，we study more cardinal invariants about the additivity and covering property of an ideal.

Definition 4.1Suppose G and I are as in the previous section，we define：

1）add＋（I）＝min｛｜T｜：T⊆G，∃A ∈I，T ＋A∉I｝，the strong additivity；

2）cov＋（I）＝min｛｜T｜：T⊆G，∃A ∈I，T ＋A＝G｝，the strong covering number.

Remark 4.2In ［41］，cov＋（I）here is denoted by covt（I），and add＋（I）is denoted byBesides，the symbol＋shall not be confused with the cardinal successor.

Fact 4.3By definition，we can expand the previous diagram to the following：

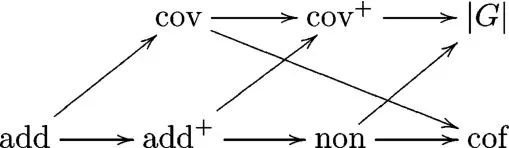
ProofWe show，for instance，that add＋≤non.Suppose that T⊆G，｜T｜＝non and T∉I.Then T＝T ＋ ｛0G｝∉I，where ｛0G｝∈I.Hence，add＋≤｜T｜＝non.

Remark 4.4At first glance，one can also define the following cardinal invariants：

1）add-（I）＝min｛｜T｜：T⊆G，∃｛At：t∈I｝⊆.

2）cov-（I）＝min｛｜T｜：T⊆G，∃｛At：t∈I｝⊆.

However，they produce nothing new.The reader can check that add＝add-and cov＝cov-.Now wepresent some less trivial results：

Fact 4.5With additional requirement on the ideal，we have：

1）if∀A，B ∈I，A＋B ∈I，then non≤add＋（So non＝add＋）；

2）if∀A，B ∈I，A＋B≠G，then non≤cov＋.

ProofWe show the first one.Otherwise add＋＜non.Let T satisfy that｜T｜＝add＋and T＋A ∉I for some A ∈I.Then ｜T｜＜non，T ∈I.This is a contradiction.

However，the assumptions of this fact fail when G is the open interval（0，1）and I is the ideal of null sets.Let A be the Cantor set，in which all numbers are represented as infinite strings of 0's and 2's in ternary fraction.Let B consists all the numbers in the interval with ternary representation as infinite strings of 0's and 1's.Clearly，A＋B＝G.A is null，similarly for B.We note that G could be the real line，and I could be the ideal of meager sets.Both A and B are also meager.

Fact 4.6［4］add≥min｛add＋，addt｝.

Corollary 4.7The following are immediate consequences of the above statement.

1）add＝min｛add＋，addt｝；

2）if add＜addt，then add＋＝add≤cov.

Fact 4.8［4］cov≥min｛cov＋，addt｝.

Corollary 4.9As corollaries，we have：

1）if cov＜addt，then cov＋＝cov≥add＋＝add；

2）if cov＜cov＋，then cov≥addt.

Definition 4.10An ideal I on G is uniform if∀B ∈I，｜B｜＜non（I）；I is weakly uniform if∀B ∈I，｜B｜≤non（I）.In other words，I is uniform iff I＝［G］＜non（I）and I is weakly uniform iff I⊆［G］≤non（I）.

The ideal N of null sets is not uniform since the Cantor set is in N but has size c.In a model where non（N）＜ c，N is not weakly uniform.Examples of such models can be built by the Random Forcing.See also ［14-15］.

Fact 4.11If I is weakly uniform，then ｜G｜＝cov·non.In particular，if I is weakly uniform，then cov＋≤cof.

ProofLet B⊆I be a covering family and｜B｜＝cov.Then G＝∪ B.

As I is weakly uniform，｜G｜≤｜B ｜·non＝cov·non.To summarize，we have the following diagram，where an arrow with dotted line represents an inequality with additional assumption：

The following fact concerns three cardinal invariants：

Theorem 4.12It is impossible that add＋＞cov＞coft.

ProofSuppose otherwise，letwith each Aα∈I.Let B be a ⊂t-dominating family.For each α，there is some Bα∈B and gα∈G such that Aα⊂ Bα＋ gα.For each B ∈B，let

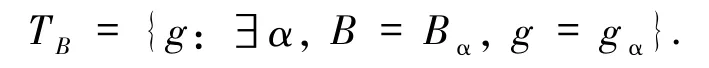
Note that ｜TB｜≤cov ＜ add＋.So B ＋TB∈I.However，This is a contradiction since ｜B ｜≤coft＜ cov.

5 An example：the ideal of countable subsets

In this section，let G＝R and I＝［R］≤ωbe the ideal of countable subsets.The cardinal invariants of the null ideal or the meager ideal will involve independence result and are beyond our discussion.We wish to present them in future work.

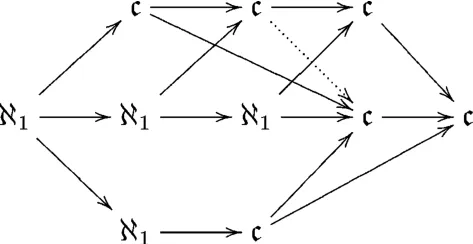
Obviously，non＝N1and cov＝c.The following theorem will decide the whole diagram.

Definition 5.1addt＝N1and coft＝c.

ProofTo see that addt＝N1，we shall construct a⊂t-unbounded family with cardinality N1.Let｛rα：α ＜ω1｝be different reals.Aα＝｛nrα：n∈Z｝∈I.For any B ∈I，let P＝｛p ∈R：∃b1，b2∈B，p＝b2-b1｝.Then P is countable and ∃α，rα∉P.Then AαtB.

To see coft＝c，let｛Aα：α ＜κ｝⊆I with κ ＜c.For each Aα，let

Pα＝｛p ∈R：∃q1，q2∈Aα，p＝q2-q1｝.

Then Pαis countable.Let P＝∪α＜κPα，then ｜P｜＝max｛κ，N0｝＜ c.Let r∈R＼P，B＝｛nr：n∈Z｝.Then B is not⊆t-bounded by any Aα.

To conclude，we have the following diagram when I＝［R］≤ω：

Here we list some questions which are not answered in thiswork.

1）Is it true that addt≤｜G｜？In the case of null ideal or meager ideal，the Borel structure actually gives cof≤｜G｜.We conjecture that addt≤｜G｜is true in general.Moreover，we guess that addt≤cov＋·non.

2）Is it true that add＋≤coftand cov≤coft？

3）Can we show the consistency of cov＋＞max｛cov，add＋｝or add ＜min｛cov，add＋｝？