数学训练“三重奏”
2020-09-21王卿
王卿

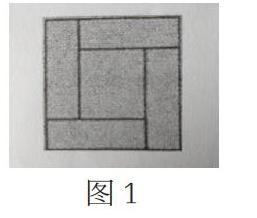
笔者所在三年级数学阶段测试中遇到了这样一道题:用4个完全相同的长方形和1个小正方形(如图1),拼成一个边长16分米的大正方形。问题(1):从图中可以看出,大正方形的一条边长是由长方形的一条( )和一条( )组成的。问题(2):每个长方形的周长是多少分米?通过读题其实不难发现,问题(1)的设置其实是为了问题(2)做铺垫的,这样可以适当降低学生的思维难度。然而笔者通过统计,得到了以下数据,引人深思:
通过以上数据的对比分析可以发现,问题(1)的正确率远高于问题(2),说明学生通过直观图形的观察,能够发现“正方形的边长等于长方形的长和宽的和”这一关系,于是问题(2)的解答应该顺势而出——既然长加宽的和是16分米,那周长不就是16×2=32分米吗?但是笔者翻阅了全年级的试卷,发现很多问题(1)对的学生,问题(2)不会做,这样一种现象引起了笔者的反思。
一、原因分析
1.反思教师的教,片面强调解题方法“机械化”,限制了学生的思维能力
“长方形的周长公式”一课的教学,教师通常会出示例题,通过小组交流讨论得出几种不同的计算方法后,进行方法优化,得出“长加宽的和乘2”这种方法。在巩固练习阶段,老师通常会引导:要求长方形的周长,必须知道什么条件?学生们会异口同声地回答“要知道长方形的长和宽,这样就能求出周长”。教师在教学中过于对知识的细化讲解,过于追求学生解题质量的心态,过多干预学生思维的举动,可能是引发这一结果的根源。
2.反思学生的学,片面关注知识技能的掌握,缺乏主动探究、创造能力
小学生的年龄特点决定了孩子的学习具有模仿性。笔者在六年级学生中做过一次随机口头调查,在被访问者中,100%的学生能脱口而出圆的面积公式,会正确解答有关圆面积公式的实际问题,但只有32%的学生会比较完整地口述出圆的面积公式的推导过程。可见,学生在数学知识的学习过程中比较关注公式的应用,而公式的推导过程在他们看来没有那么重要,甚至有少部分学生会认为只要会解决问题就行。由此可以推想,学生在课堂教学中,数学知识技能的学习是他们听课关注的焦點,练习中的巩固也是形成熟练解题技能的必要训练。因此考试中才会出现如上问题,虽然问题(1)会解答,但回到求周长的问题时,学生仍然调动以往机械性的解题经验,首先就在寻找长和宽。试卷上还出现一部分学生把16分米拆分成12分米和4分米,然后再求周长,这些画蛇添足的做法实在不可取。这再次印证了学生的思维比较僵化,不够灵活多变。
二、辩证地把握数学训练与发展思维的关系
1.科学设计练习,发展学生思考力
科学的、一定数量的数学练习能促进学生理解,发展数学思维,反之,单一、重复的机械性训练,会限制学生的思考力。日常教学中,教师应有层次地设计练习,做到基础训练与变式训练并重,这样才能真正发展学生思考力。
只有教师在教学中注意题目的变化,减少单一训练,拓宽学生的思维空间,关注学生的数学思考,强调解题策略,这样学生的解题方式才会由“单一”变“多样”。
2.引导自主探索,发展学生的创造力
数学家华罗庚指出,对书本中的定律、公式问题,我们不仅应该记住它的结论,更应懂得它是怎么来的,明白经历了多少曲折、攻破多少难关才得出这个结论的。如在教学“圆的面积公式”这一课时,教师应留有充分的空间和时间,让学生自主经历知识形成的过程。课前预学单导学,让孩子课前根据预学单提示动手剪下书后16等分、32等分的圆,再拼一拼,思考:剪下的图形能拼成什么图形?拼成的长方形与原来的圆有什么关系?课中借助预学单助学,在四人小组里结合直观图边演示边交流,让每个孩子有充分的时间说出圆面积公式的推导过程。教者再借助动画演示,让学生再次感受将圆转化成长方形的过程中所蕴含的数学极限思想,更透彻地掌握了用转化的策略推导圆面积公式,建构新旧知识间的联系。这样才能避免解题中单一应用公式、生搬硬套的尴尬。
3.重视解题反思,提升学生学习力
郑毓信教授曾在《“数学核心素养”之我见》一文中指出,我们应当注意纠正的一个现象:我们的学生一直在做,一直在算,一直在动手,但就是不想!确实,作为一名一线教师,也常常遇到这样的苦恼,你花了很大的力气评讲订正过的题目,仍然有部分孩子解答是错误的,更可恼的是,这些孩子常常连自己错在哪里都不思考,只是人云亦云地跟着订正,形成低效学习。因此,在数学学习过程中,应引导学生自觉地检查自己的思维活动,反思自己是怎样发现和解决问题的,应用了哪些基本方法、技能和技巧。
如在平时的作业中要求学生针对自己的错误,进行局部反思,避免直接抄正确答案的“假订正”。尤其是填空题、选择题的订正,要求学生在旁边写出完整的解题步骤,可以列式、画图;判断题要求学生将错误的抄一遍,在旁边将正确的也写一遍。在进行阶段测试后,试卷上的错题要求学生抄题订正,进行深度反思。
综上所述,学生经历一定的富有变化、联系实际的数学问题的训练时,只有仔细审题、主动探究,自觉进行解题反思,才能抓住对象的本质,理解解题过程中的方法和策略,才能真正发展学生的数学思维能力。
