Fe−Mn−(Al)−C高强韧性钢氢脆微观机制的研究进展

章小峰，万亚雄，武学俊，阚中伟，黄贞益

1) 冶金工程与资源综合利用安徽省重点实验室（安徽工业大学），马鞍山 243002 2) 安徽工业大学冶金工程学院，马鞍山 243002

随着第二代、第三代高强汽车钢的抗拉强度超过1000 MPa，随之而来的是高强钢的延性断裂问题愈发突出[1−2]. 在对高强钢延性断裂检测分析中，往往伴随着氢脆（Hydrogen embrittlement, HE）、氢蚀、氢鼓泡、白点或发纹、显微穿孔、流变性能退化和形成金属氢化物等，极大地损伤了钢基体的性能[3−4]. 钢的强度级别越高，对氢越敏感，对其服役造成了严重的制约[5].

目前，Fe−Mn−C 系、Fe−Mn−Al−C 系等含Mn 量高的汽车结构用钢正受到极大的关注，各种强韧化机制的高强韧钢层出不穷[6−10]. 早期的 Fe−Mn−C系 TWIP 钢（Twinning-induced plasticity，TWIP）借鉴了作为耐磨钢的高锰钢[11]，再通过添加Al元素进行轻量化设计成 Fe−Mn−Al−C 系 TWIP 钢或低密度钢（往往含Al质量分数>3%），往往被用在B门柱上. 通过相变、孪晶、微带、晶粒细化、第二相析出等方式实现高强韧性的同时，也给加工、服役过程中氢元素依附钢基体提供了便利的通道和陷阱，容易造成延迟断裂[12−13].

本文试图从氢与晶体缺陷微观作用机制的角度对 Fe−Mn−(Al)−C系高强钢中氢陷阱类型与特征、氢与钢中缺陷的交互作用、以及氢脆模型的表达和评价方法等方面进行综述，以期对该类高强钢的氢脆及服役性能研究更加清晰、深入.

1 Fe−Mn−(Al)−C 高强韧性钢中的氢陷阱

在服役环境中大量氢离子的作用下，氢不仅存在于基相、第二析出相和夹杂物中，也在晶体缺陷（如空位、位错、层错、晶界、相界等）中偏聚，如图1所示[14]. 通常，氢原子、氢离子在钢材表面通过物理吸附、化学吸附、溶解、扩散等过程才得以进入到钢基体某个位置，形成氢原子团、正负氢离子或氢分子. 由于氢原子直径最小，容易流动到钢基体缺陷部位，如应力集中区和位错密集区、晶体点阵的间隙位置，以及气孔、微裂纹、晶界、相界、非金属夹杂物等处.

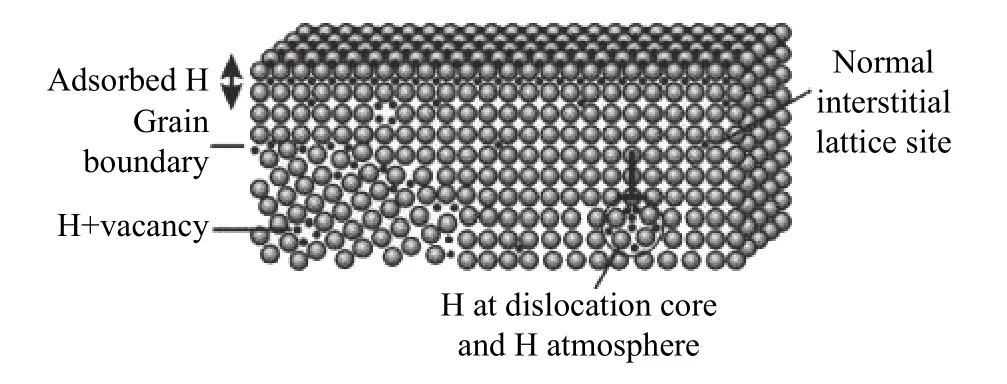
图1 晶体缺陷中氢脆现象及示意图[14]Fig.1 Hydrogen embrittlement phenomena and mechanisms[14]

在内应力、应变或温度变化等作用下，溶解在钢基相中的氢与第二相、晶体缺陷、夹杂物交互作用，部分氢在扩散时被某些缺陷捕捉，形成氢陷阱[15−16]. 部分暂储在陷阱中的氢借助扩散通道逃逸出陷阱，形成流动氢原子并择址富聚. 作用持续时间越长，聚集在局域内的氢就会越多，越容易诱发氢致脆断[17].

1.1 Fe−Mn−(Al)−C 系钢的组织结构特征

1.1.1 奥氏体、铁素体与马氏体

Fe−Mn−(Al)−C 系高强韧钢中 Al元素不仅降低了合金密度，还提高了合金层错能，有利于孪晶的形成[18−19]. Al元素还扩大了钢的晶格常数，影响到钢中同素异形体的热力学稳定性. 当钢中Al含量较多，需要添加较多的C元素进行复相组织的调控与平衡，且因Al元素的增加易发生奥氏体调幅分解，生成κappa碳化物，影响到热处理时C和Mn在基体中的分布状态和其它析出相的生成. 依具体成分和工艺不同，其基体组织主要有FCC奥氏体、BCC铁素体和HCP马氏体等，其晶格参数、原子半径r和原子间隙如表1所示[20].

受金属晶格中的占位和扩散能垒的影响，氢在各基相中扩散速率和固溶度也各不相同[21−23].就原子晶格排布而言，BCC晶格较FCC、HCP晶格明显要松弛，氢原子在BCC晶格中的扩散系数也最大，具有极高的可流动性[24]. 通过第一性原理计算（The ab initio calculation），在不同绝对温度（T）条件下，得出氢在BCC、FCC和HCP晶体的扩散系数分别为1.379×10−4e(−1120/T)cm2·s−1、 3.22×10−4e(−8425/T)cm2·s−1和 6.161×10−4e(−8830/T)cm2·s−1[25].

表1 α-Fe、γ-Fe 和 ε-Fe 的晶格特征Table 1 Crystallographic characteristics of α-Fe，γ-Fe, and ε-Fe structures

就晶体结构而言，FCC、BCC、HCP晶体中均存在四面体（Tetrahedral site，T位）和八面体（Octahedral site，O 位）两种类型的间隙，如图 2 所示[25]. 只不过各晶体结构中的T位、O位间隙大小不一样，氢原子迁移其间的难易程度不一. 因氢原子半径为0.037 nm，故FCC、BCC、HCP晶格间隙中比较适合氢原子的位置分别是O位、T位、O位.

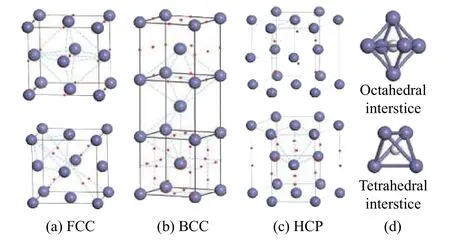
图2 铁的三种晶体结构[25]. （a）面心立方结构；（b）体心立方结构；（c）密排六方结构；（d）H在八面体和四面体间隙Fig.2 Three crystal structures of iron[25]:(a) face-centered cubic structure; (b) body-centered cubic structure; (c) close-packed hexagonal structure; (d) diagrams of H in octahedral and tetrahedral interstices

就抗氢能力而言，通常HCP结构>FCC结构>BCC结构. 在BCC晶体中，氢原子稳定扩散路径是从四面体间隙迁移到最近的四面体位置（T—T）；在FCC、FCT晶体中，氢原子稳定扩散路径沿O位—T位—O位；在HCP铁晶体中，氢原子稳定扩散路径是从O位—O位，氢扩散的迁移能比在FCC晶格中高，这导致了H在HCP晶格中的低扩散率，且氢在HCP晶格中扩散具有依赖于c/a比的各向异性[23]. 鉴于钢的晶体结构与成分、温度密切相关，氢原子在不同状态钢中的溶解度、扩散也随之变化，影响到氢原子在BCC、FCC、HCP各晶体结构中位置及迁移所需能量[26−27]. 图3描述了氢原子在各晶格中不同位点及迁移路径，其能量消耗与氢的迁移路径有关[23,28]，表2描述了H在各晶体中扩散的迁移能[23,25].

1.1.2 第二相

在 Fe−Mn−(Al)−C 系高强韧钢中，当 Al质量分数低于3%时，主要是存在大量孪晶的奥氏体钢.当Al质量分数较高时（3%～13%），往往在奥氏体或铁素体基体中析出κappa碳化物、金属间化合物（B2、DO3型 Fe−Al相）、β-Mn等第二相[29].κappa碳化物是一种钙钛矿立方晶体结构，由Al原子占据立方体的八个顶角，Fe原子占据六个面心位置，C原子处于立方晶胞的中心位置，分子式为 Fe3AlC；Fe−Al型 B2、DO3相是一类易从 α铁素体中析出的BCC晶格点阵，分子式分别为FeAl、Fe3Al；β-Mn是一种立方结构的锰元素异构体，β-Mn每个晶胞中有20个原子，Wyckoff晶体学位点为8c和12d，容易与γ-Fe共存[30]. 在服役过程中，此类析出相与氢作用密切，对钢材塑韧性有极大的损伤[31].

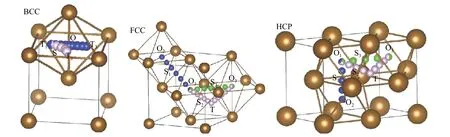
图3 氢原子在 BCC、FCC 和 HCP 晶格的迁移路径[23, 28]Fig.3 Migration path of hydrogen atom in BCC, FCC, and HCP crystalline lattices[23, 28]

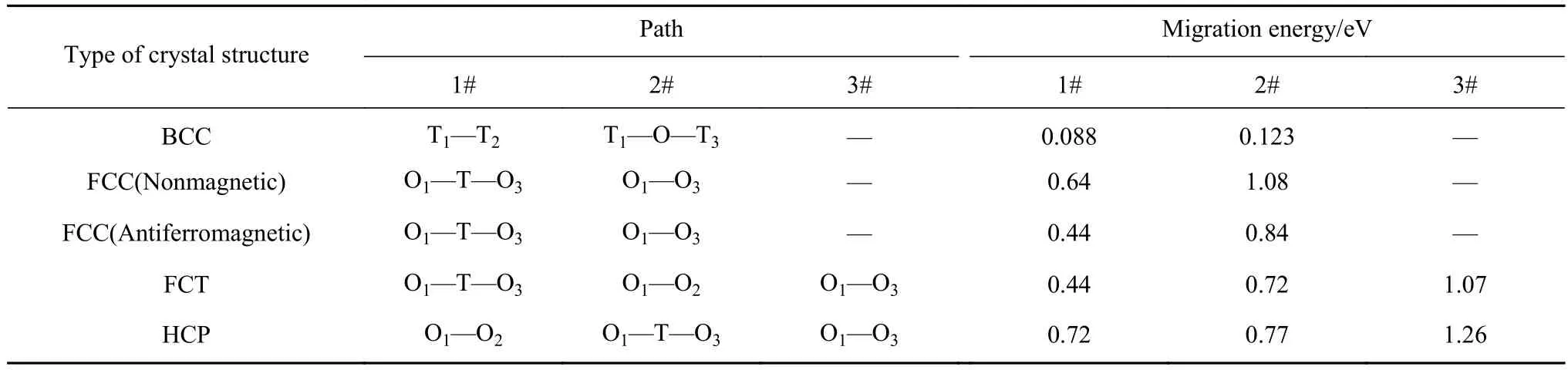
表2 氢在 BCC、FCC、FCT 和 HCP 中扩散的迁移能Table 2 Migration energy of hydrogen diffusion in BCC, nonmagnetic FCC, antiferromagnetic FCT, and HCP

1.2 晶格缺陷

氢溶解在 Fe−Mn−(Al)−C 系钢基体后，将与钢的各种晶体缺陷（如间隙位置、空位、位错、层错、晶界、微孔等）及析出粒子、夹杂物等相互作用，并利用钢中的各种通道或陷阱进行扩散、聚集.

1.2.1 空位与溶质原子

在Fe−Mn−(Al)−C 系钢变形和热处理过程中，形成B2型FeAl相会产生大量热空位、反位原子缺陷，在室温α-铁素体基中仍然能保持较高浓度[32].研究表明，B2型FeAl相点缺陷中，Fe空位和Fe占据Al格点的反位缺陷（FeAl）浓度随Al含量的增加而增加. 氢在B2型Fe−Al相中可能占据的间隙位置有三种：分别是四面体间隙位（T）、2Fe4Al的八面体间隙位（O1）以及2Al4Fe的八面体间隙位（O2）[31, 33−34].

1.2.2 位错与层错

堆垛层错（Stacking fault, SF）是晶体结构中不同于正常排列顺序的堆垛错排，由两个Shockley不全位错形成的面缺陷，不仅在FCC、HCP、BCC晶体结构中存在，对于结构较复杂的金属间化合物，其内部也会出现堆垛层错. 以FCC晶体为例，若晶体结构的{111}密排面的堆垛顺序发生了改变，产生了一个将基体分为两部分的界面，如图 4（a）所示[35−36]. 由于化学键的变化，堆垛层错可以被视为一种特殊的Gibbs界面，此界面是由基体中各层之间的层间距和堆垛层错相（Stacking fault phase，SFP）的层间距差造成的，如图 4（b）所示[35−36].

1.2.3 孪晶与晶界

当孪晶界成为氢陷阱时，需要局部应变场俘获氢原子. 如图5所示[38]，移动的变形孪晶尖端的应力集中刚好提供了这种局部应变场，将氢吸引到障碍变形孪晶边界. 因此，孪晶应力集中场对于氢的局部化以及晶界和孪晶界处裂纹的萌生至关重要.

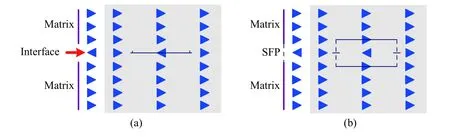
图4 FCC 晶体中的层错堆垛示意图[35-36]. （a）无限层错；（b）两个不全位错为界的终止层错Fig.4 Schematics of stacking faults in an FCC crystal described by stacking operators[35-36]:(a) an infinite stacking fault; (b) a terminated stacking fault bounded by two partial dislocations

氢在不同晶界结构中的溶解能较大程度上取决于间隙位置的局域配位，且与间隙位置的实际体积V适度相关. 在密堆积结构的低能∑3晶界中，可用的间隙位置与T位、O位非常相似. ∑3界面相当稳定，不利于氢的富集. 在开放晶界结构中，BCC∑5界和FCC∑11晶界有利于为氢原子提供不同的填隙位置，将氢捕获在晶界处. 通常而言，没有哪种晶界能为氢原子提供快速扩散通道，但较开放的结构（BCC∑5和FCC∑11）有利于氢原子沿晶界面扩散，从而可以将氢扩散到其它缺陷，如晶界结合部位（某种界面的中间（Intermediate,im）和界面（Interface, if）的间隙吸附位）或位错，如图6描述了BCC、FCC晶体中各种晶界中氢溶解能ΔE[39].

1.3 特殊元素的作用

成分设计时，除考虑 Fe−Mn−(Al)−C 钢主成分以外，往往由于某些特殊性能要求，还会在主成分基础上再添加其它某种元素，如 Si、Re、Cu、P、V等[40−42]. 这些少量元素的加入，有时不仅改变了基相、第二相的构成、比例、形态等，也会改变晶体缺陷的类别、数量，对钢材的氢陷阱位置、氢扩散、氢致损伤机制等有着直接的影响[43].

2 高强韧性钢中的氢脆

钢中的氢从其冶炼就开始存在，在成形、服役过程中，有氢环境还会继续与钢基相互作用. 一般而言，钢中氢的质量分数在 5×10−6～10×10−6时就会产生HE裂纹，但对于超高强度钢，其临界氢含量要低得多，有的甚至只有 0.1×10−6～1×10−6也会发生氢致断裂[44].

2.1 钢中氢的渗透、溶解与扩散行为

在有氢环境中，氢分子主要通过表面吸附、氢分子离解、氢原子吸附等物理化学反应过程向钢中渗透. 另外，在阴极电解充氢时，在钢材表面上析出的原子氢也能扩散进入基体. 氢在钢中可能形成固溶体、氢化物、分子状态氢气，也可能与金属中的第二相进行化学反应而生成气体产物（如“甲烷反应”）. 钢材服役过程中，氢与各类陷阱的结合、激活随能量起伏而在钢中扩散、聚集，图7是各种状态的氢在钢中的渗透、溶解与扩散与能量关系的示意图[45−47].

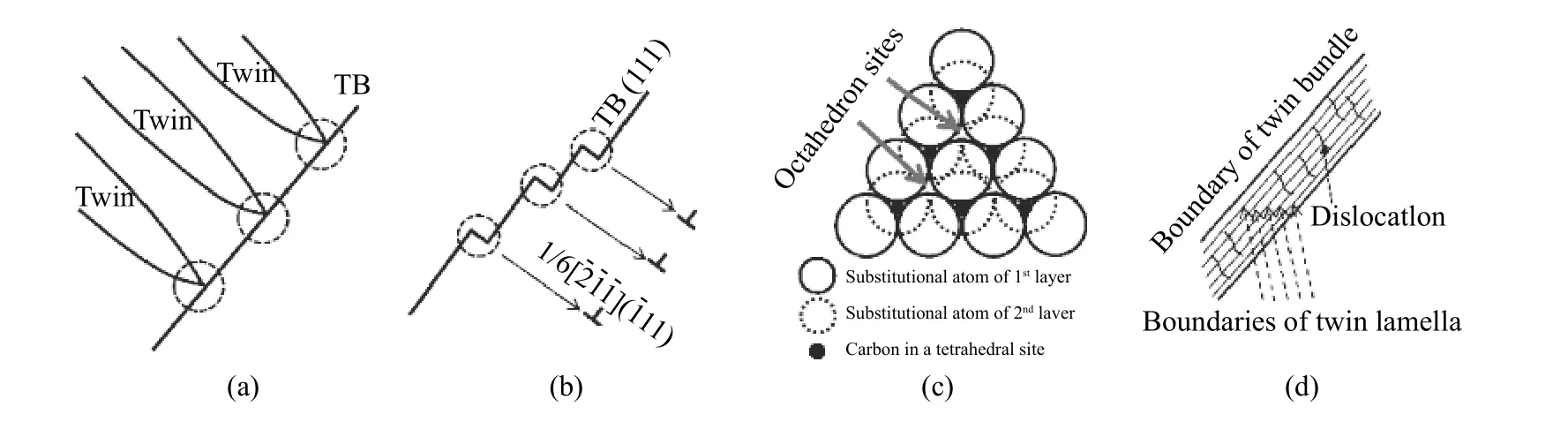
图5 变形孪晶界氢俘获示意图（TB：孪晶界）[38]. （a）变形孪晶尖端的应力集中；（b）位错孪晶交叉形成的台阶处的应变场；（c）伪孪晶形成引起的晶格畸变；（d）变形孪晶的纳米结构，包括位错和纳米孪晶带Fig.5 Schematics describing the factors affecting hydrogen trapping at the deformation twin boundaries (TB:twin boundary)[38]:(a) stress concentration at a tip of a deformation twin; (b) strain field at the steps formed by the dislocation-twin intersection; (c) lattice distortion due to pseudo-twin formation;(d) nanoscale structure of deformation twins, including dislocations and nanotwin plates

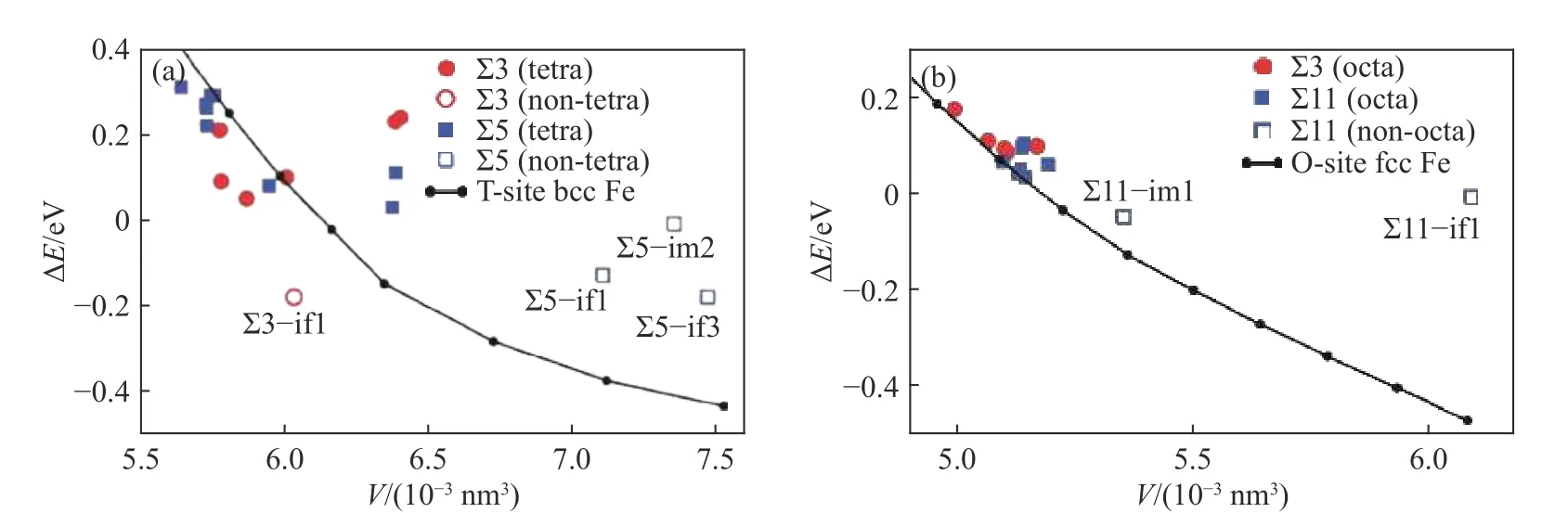
图6 氢在不同位置的溶解能[39]. （a）BCC 铁中的四面体位和 BCC∑3, BCC∑5 晶界内各种中间 (im)和界面 (if)的间隙吸附位；（b）FCC 铁中的八面体位, FCC∑3和FCC∑11 Fe晶界内各种中间(im)和界面(if)的间隙吸附位Fig.6 Solution energy of hydrogen as a function of the volume of the interstitial site[39]:(a) tetrahedral sites in BCC Fe and various intermediate (im) and interface (if) interstitial adsorption sites within BCC∑3 and BCC∑5 Fe grain boundaries; (b) octahedral sites in FCC Fe and various intermediate (im) and interface (if) interstitial adsorption sites within FCC∑3, and FCC∑11 Fe grain boundaries

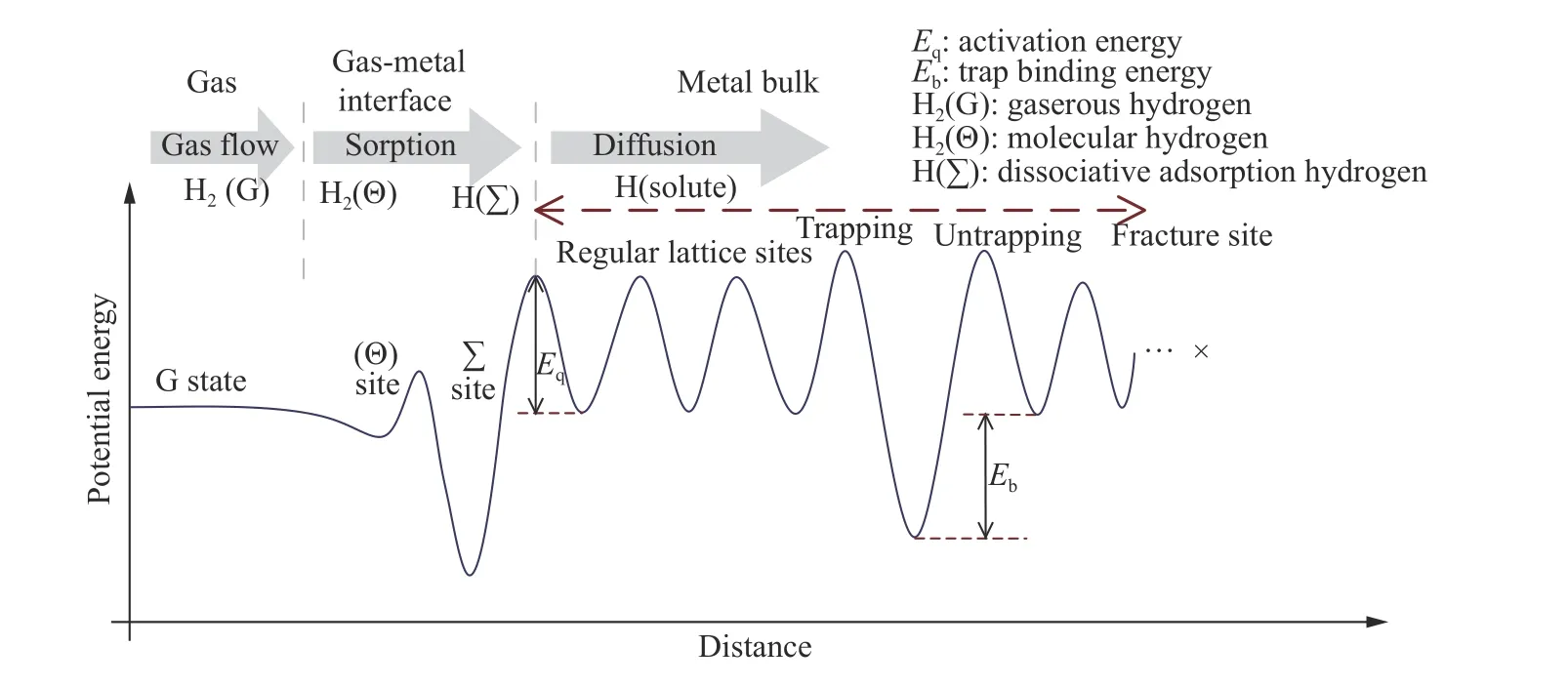
图7 氢−金属平衡中的能量关系及氢在不同位置的迁移示意图Fig.7 Schematic view of the energy relationship in hydrogen−metal equilibria and hydrogen migration in different sites

氢在钢中的渗透、扩散和固溶与氢在各种陷阱的结合能、激活能直接关联. 如果陷阱结合能Eb较小（一般<60 kJ·mol−1），氢就容易从陷阱中逸出而进入间隙原子位置，形成可逆陷阱. 相反，若Eb较大（≥60 kJ·mol−1），则氢难以从陷阱中逸出，形成不可逆陷阱. 钢材在服役时往往是在室温，可逆陷阱将对HE的作用更加明显. 此外，氢在各缺陷中的能量状态受局部组织内的压力、温度的作用，影响到氢在钢中的扩散、聚集行为. 表3是氢与钢中空位、主要元素、晶体结构缺陷及析出相的结合能[25,48−49]. 在 Fe−Mn−Al−C 钢中，氢在各种缺陷中的激活能也对其扩散、捕获及富聚作用明显，如表 4 所示[50−53].

2.2 氢与高强钢组织的交互作用

氢在钢中扩散迁移过程中，会与各种陷阱（晶体内的间隙、空位、晶界、相界、位错、层错、析出相、夹杂物等）交互作用，不仅影响到氢在钢中的分布和聚集程度，还会对相的稳定性和材料强韧性能产生重要的影响.

2.2.1 氢与晶格缺陷的作用

氢原子不仅在各晶体的T位、O位之间迁移，更与α-Fe，γ-Fe和ε-Fe晶体结构中某些空位、置换位等点缺陷相互作用. 以BCC晶体为例，根据第一性原理计算，钢中氢在晶体置换位和间隙位的形成能也不一样. 表5为氢在α-Fe，γ-Fe和ε-Fe中的T位、O位间隙、空位及置换位中的形成能[25−26].

Fe−Mn−(Al)−C 钢的室温组织以 α-Fe或 γ-Fe居多，氢的存在显著增强了位错迁移，也存在氢与位错核之间的强结合. 因TWIP钢中存在大量的孪晶带，而含Al低密度钢中层错、位错密集. 在小应变条件下，位错滑移与薄片孪晶交互作用有利于应变硬化，当氢参与交互作用时，在低应变率下孪晶界发生明显扭曲，变形的孪晶界角部使孪晶界面俘获了氢，而氢促进了孪晶界面开裂，充氢后其断裂模式由韧性断裂转变为低应变率的准解理断裂，而高应变率下较少观察到解理断裂，如图8所 示[13, 54].

TWIP钢氢致开裂可分为沿晶界开裂和孪晶界辅助开裂，孪晶开裂占约25%，但变形孪晶界处裂纹是TWIP钢发生HE的关键. 晶间裂纹的优先起始点是变形孪晶界与三叉晶界. 应力集中于变形孪晶尖端，有助于裂纹在两个部位的扩展，如图9所示[38].

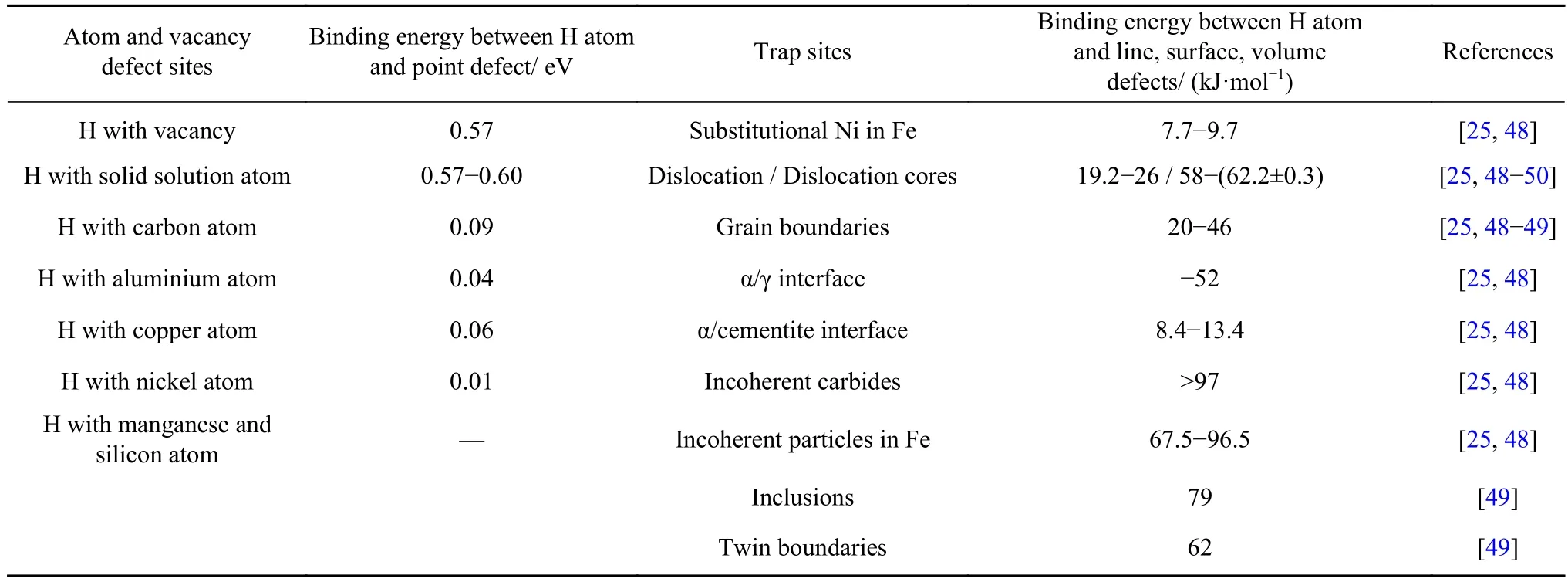
表3 氢与钢中元素、空位及陷阱位的结合能Table 3 Elements and vacancy in steel and selected trap sites binding energy values of H in steel

表5 BCC、FCC 和 HCP 晶体中不同位置的氢形成能Table 5 Formation energy of H in different sites of BCC, FCC, and HCP Fe crystal

图8 缺陷形成、氢偏析、孪生应力集中和开裂的顺序过程示意图[13, 54]Fig.8 Schematic of the sequential process of defect formation, hydrogen segregation, twinning-induced stress concentration, and cracking[13, 54]

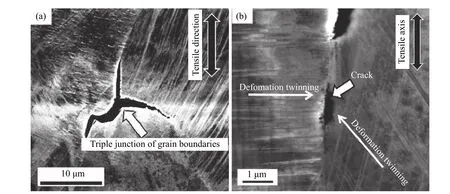
图9 三叉晶界与变形孪晶界的裂纹起源[38]. （a）三叉晶界；（b）变形孪晶界Fig.9 Crack initiation from a triple junction of grain boundaries and a grain boundary intercepting deformation twinning[38]:(a) a triple junction of the grain boundaries；(b) a grain boundary intercepting deformation twinning

Casillas等[55]利用像差校正扫描透射显微镜，揭示了某含Al高Mn TWIP钢的孪晶不仅可以通过本征层错形核，还通过高应变拉伸证明了非本征层错作为孪晶形核的可行性. Khedr等[56]对Fe−12.5Mn−1.2C钢的研究表明：经过冷轧后闪速退火，奥氏体基体中获得一定数量的纳米孪晶，提高了抗HE性能. 通过对充氢冷轧样品进行预拉伸和带缺口试样进行拉伸发现，纳米孪晶对阻止位错滑动、抑制裂纹萌生/扩展有显著影响，延迟了裂纹发生的时间，如图10所示.

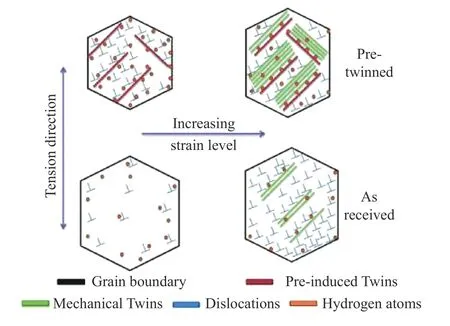
图10 预诱导孪晶阻碍冷轧样品充氢后位错滑移的示意图Fig.10 Graphical illustration showing the effect of preinduced twins on preventing dislocation slip after H-charging in cold-rolled sample

对 Fe−18Mn−0.6C−1.5Al钢的充氢实验表明[57]：添加质量分数1.5%Al（简称1.5Al）不会显著影响TWIP钢的氢脆性能，但含Al的TWIP钢能够抑制氢进入并具有较大的总延伸率，提高了杯形试样抗氢脆性能. 这可能是由于氢容易在含Al的Fe−Mn−C钢表面形成一层致密氧化铝层阻碍了氢的进入，且钢基体的氢溶解度增加，局域残余应力降低，导致特定晶界处能富集更多的氢，增强了HE抵抗力.且Al降低了氢吸收和腐蚀动力，也增加了抗HE性能，不同含Al量的TWIP钢的充氢吸收率与温度关系，及氢扩散量与断裂应力关系见图 11[13,42,58].

随着Al含量的增加，含Al的TWIP钢中的扩散氢捕集位点少. 机械孪晶分布更均匀，并形成了较强的〈111〉和〈100〉织构，氢随可动位错长程输送的能力降低，降低了氢扩散的驱动力[57−59].Al含量增加不仅显著地降低了钢材密度，也呈现了不同的强韧性机制，钢中的Al对氢脆的影响也会不同. 对奥氏体基 Fe−26Mn−11Al−1.2C 充氢研究表明：氢致断裂机制主要为三叉晶界开裂和滑移辅助晶界开裂，前者在FCC晶体中较常见，后者与含有 κappa碳化物的 Fe−Mn−Al−C 内的滑移局部化导致沿晶界形成空洞，引起微观韧性晶间开裂和宏观脆性断裂有关，如图12所示[13,51].

在晶界处偏聚的氢不仅会影响晶界的强度，也会对不同晶粒尺寸的晶界处氢扩散、晶界运动影响巨大. 不同晶粒度 Fe−31Mn−3Al−3Si钢的充氢实验表明晶粒越细小，氢富集程度越低[49]. 这主要因为晶粒细小时，单位体积的晶界面积越大，晶界上的氢含量也就越低，氢扩散量就越大，越不容易引起氢集中，延缓了裂纹的产生，表6计算了不同晶粒度晶界处的氢扩散.

2.2.2 氢与析出相的作用

对于低 Al高 Mn 含量的 Fe−Mn−Al−C 钢，变形时存在大量孪晶，其强化机制主要是TWIP，且在奥氏体晶界处易析出M3C型碳化物[8]；而高Al高 Mn 含量的 Fe−Mn−Al−C 钢，具有很高的层错能，机械孪晶大大减少，往往析出大量κappa碳化物[60]. 晶界M3C型碳化物明显倾向于晶间断裂，而Al的加入抑制了晶界渗碳体的形成，显著提高了延迟断裂的抗力. 而氢对钢中κappa碳化物Fe3AlC、DO3型析出相Fe3Al的作用表明：其脆化行为与合金中的碳含量有关，低碳合金（C质量分数<0.05%）的氢脆发生在Fe3Al相，高碳合金（C质量分数≥1%）的氢脆发生在枝晶间区，且基体因含有Fe3AlC碳化物而氢脆，但Fe3AlC碳化物限制了裂纹的扩展[61].

鉴于κappa碳化物的化学式构成及晶体结构特征，氢易于与其结合形成一种较为稳定氢化物（Fe3AlH）. 基于密度泛函理论（Density-functional theory, DFT），Timmerscheidt等[62]计算了 κappa 碳化物与溶解在其中氢的相互作用，H-H的相互作用在短距离内表现出强的排斥力，而C-H在长距离内表现出强的排斥力，且直接相邻的碳和氢原子抑制了长程相互作用. κappa碳化物捕获扩散氢的效率取决于C和Mn的含量，决定了空位C的κappa碳化物的数量，从而决定了捕获氢的容量，而Mn含量决定了整体捕获效率. 故要控制κappa碳化物中氢的扩散，应该提高κappa相中C含量的同时降低Mn含量. 此外，若κappa碳化物/奥氏体界面附近存在空位时，则κappa碳化物和基体界面的氢具有很高的溶解性，从而使κappa碳化物/奥氏体界面成为氢的有效捕集中心.

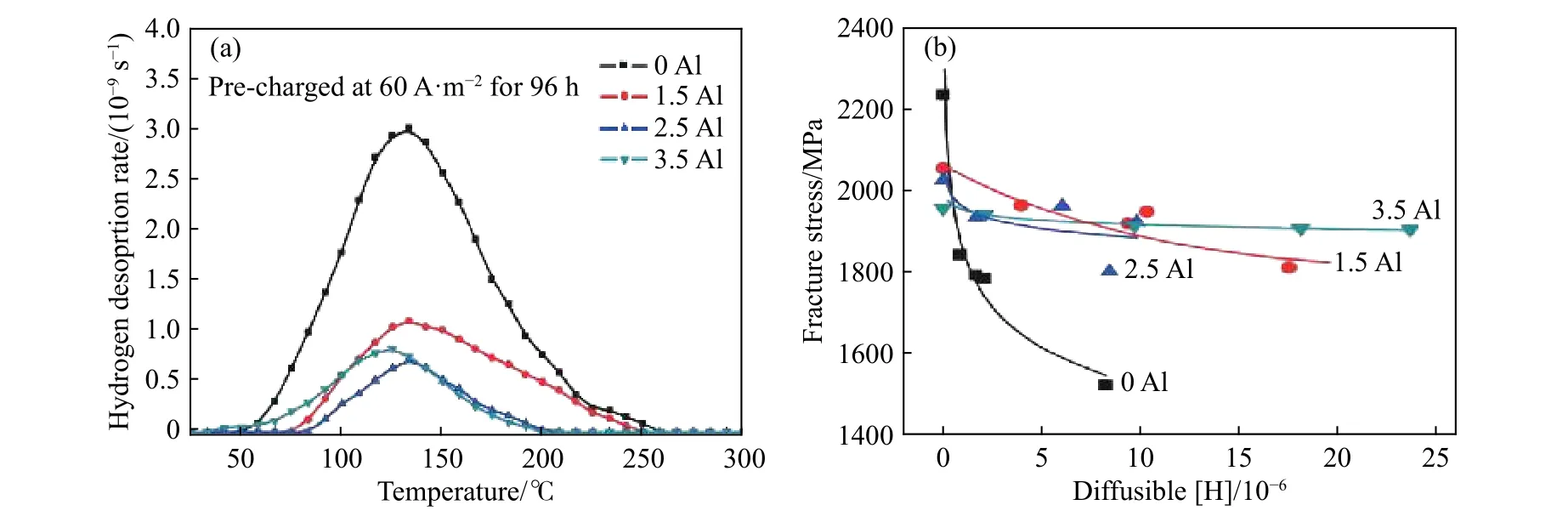
图11 Fe−18Mn−xAl钢的热解吸分析（TDA）曲线和断裂应力[13, 42, 58]. （a）相同充氢条件下的 TDA；（b）不同扩散氢条件下缺口试样的断裂应力Fig.11 TDA profiles and fracture stress with different Al contents in Fe−18Mn−xAl steels[13, 42, 58]:(a) TDA profiles at an identical hydrogen charging condition; (b) plot of fracture stress of notched specimens against diffusible hydrogen content

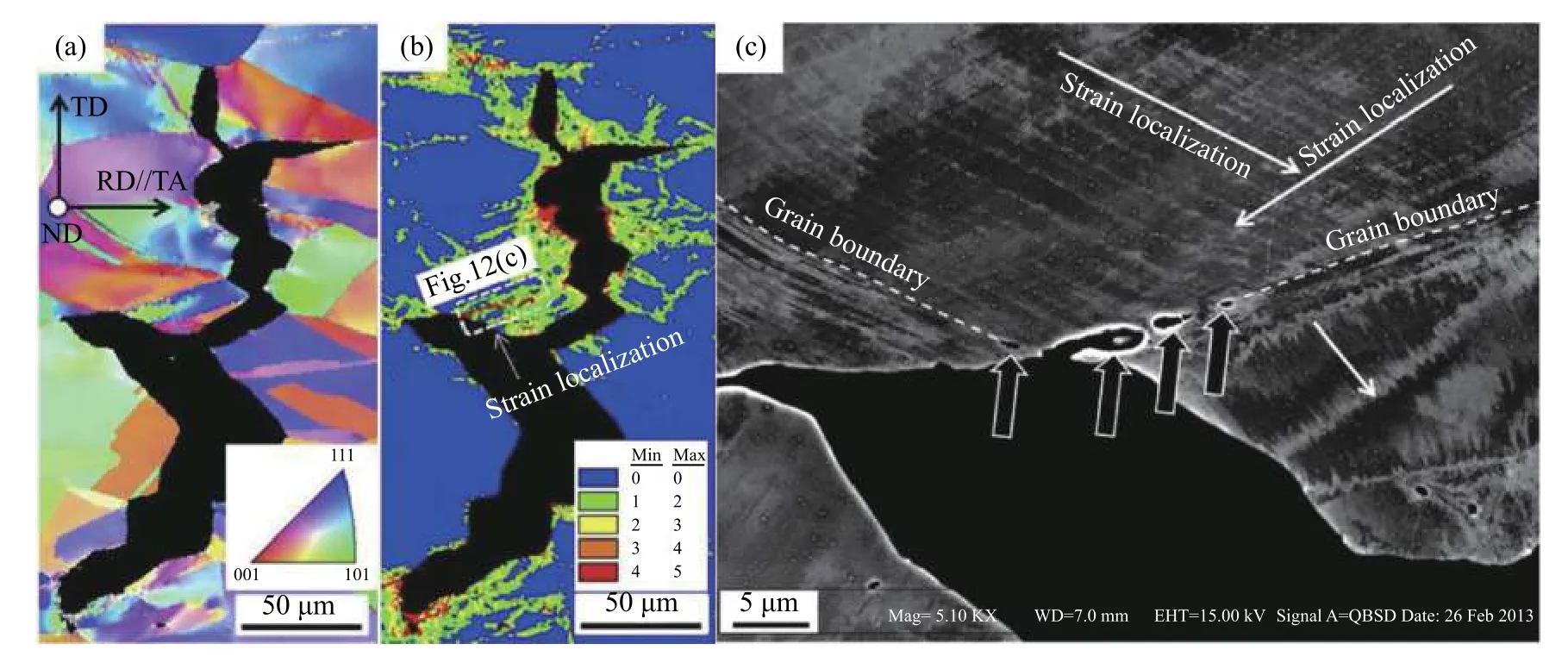
图12 含 κappa 碳化物 Fe−26Mn−11Al−1.2C 奥氏体钢的氢致晶间裂纹[13, 51]. （a）反极图（IPF）；（b）充氢条件下的 KAM 图；（c）晶间裂纹形成Fig.12 Hydrogen-induced intergranular crack in Fe−26Mn−11Al−1.2C austenitic steel containing κ-carbides[13, 51]:(a) inverse pole figure (IPF);(b) kernel average misoritation（KAM）maps under hydrogen charging; (c) intergranular crack formation

表6 晶界处氢扩散的计算数值Table 6 Calculated values of hydrogen diffusion at grain boundaries

此外，在一些高强韧性钢中，通过添加C、N、Ti、V、O等形成一些碳氮析出物或氧化物阻碍氢渗透，影响着此类钢的氢损伤行为[1,63−64]. 由于不是 Fe−Mn−(Al)−C钢主成分体系的常规析出物，在此不做详细论述.

3 氢脆模型机制表达与评价

3.1 模型与机制

3.1.1 氢扩散热力学模型

从热力学角度来看，钢基体晶格中存在的氢一直都在其热力学平衡位置附近作热振动，当其振动能量高于扩散激活能时，将从一个间隙位置跃迁到另一个间隙位置，引起其附近晶体点阵产生局部的弹性畸变和熵变，从而引起氢的迁移，如式（1）～（3）所示[27].

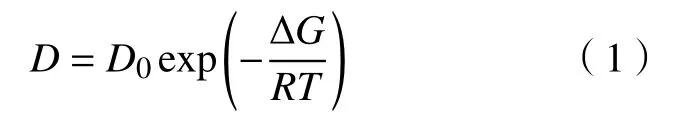
式中，D为晶体 中原子 扩散系 数 ，∆G为扩 散原子Gibbs自由能差，R为气体常数、T为绝对温度.

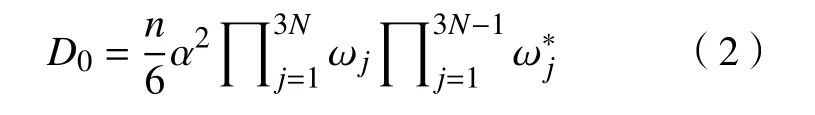
式中，n为 等效跃迁路径数量的几何因子，α为跃迁距离，N为 间隙配位数，为扩散原子在初始状态和过渡状态下的固有振荡频率.

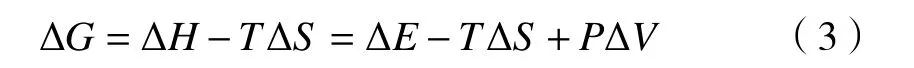
式中，∆E为扩散激活能，∆H为扩散激活焓，∆S为扩散激活熵，∆V为扩散激活体积，P为静液压力.

本质上，氢扩散过程与钢中的化学势密切相关，在化学势能差的驱动下，氢将从化学势高的地方向化学势低的地方扩散，直至达到平衡. 按照Fick定律扩散方程，如式（4）、（5）所示，氢的扩散通量J（单位时间内通过单位面积的扩散物质的量）与氢梯度浓度成正比. 式（6）、（7）分别描述钢中稳态氢的渗透率和固溶度[46,65].

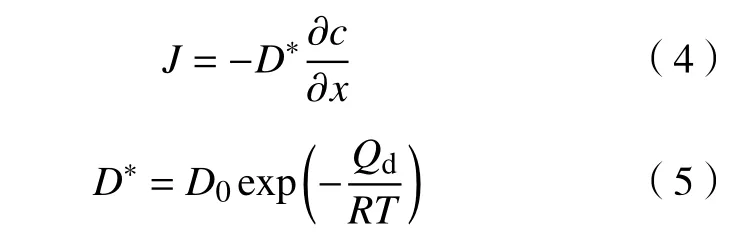
式中，D∗为稳态扩散系数，为氢浓度梯度，Qd为扩散激活能，R为 气体常数、T为绝对温度.

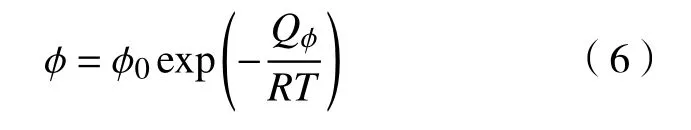
式中，ϕ为稳态渗透系数，ϕ0为渗透频率因子，Qϕ为渗透激活能.

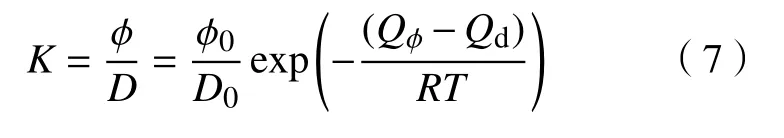
式中，K为稳态固溶度.

3.1.2 作用机制

氢在金属中引起塑韧性损伤的机制主要有：弱键理论，也称为减聚力理论（Hydrogen-enhanced decohesion, HEDE）、氢吸附促进位错发射理论（Adsorption-induced dislocation emission, AIDE）、氢促进塑性局部化理论（Hydrogen-enhanced local plasticity, HELP）等. 在氢与晶体缺陷交互作用时，氢脆往往由几种机制共同作用而导致，其在钢中的作用机制可以用图13表达[66].

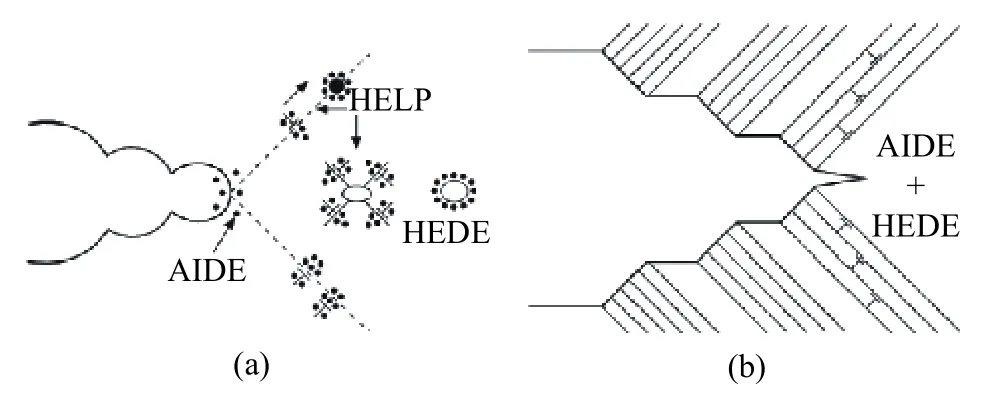
图13 氢辅助裂化混合机制的示意图[66]. （a）HELP 与 HEDE 机制共同作用下的AIDE机制；（b）AIDE与HEDE机制Fig.13 Schematics illustrating the hybrid mechanisms of hydrogenassisted cracking[66]:(a) AIDE with contributions from HELP and HEDE;(b) AIDE alternating with HEDE

由于HEDE源于热力学和第一性原理，对钢中晶界、界面处氢浓度较高的区域，氢降低了金属键能，促进了晶界开裂；而AIDE机制揭示了氢在裂尖表面的吸附可以弱化几个原子层距离厚度内的原子键，促进位错形核与运动. 如果位错发射过程被抑制，则材料更容易发生解理开裂. 如氢的侵入会促进Fe−Al体相中位错的发射、增殖和滑移，从而出现局部塑性变形[67]. HELP机制则由两方面引起：1）氢增加了位错迁移率，导致材料软化；2）H减少了位错−位错的相互作用，促进位错平面滑动和塞积，导致初始损伤[68−69]. 在氢原子与Fe−Mn−Al−C 钢的晶界作用时，可以观察到氢原子倾向于先在三叉晶界形核，应变局部化发生在晶界上；氢进而与发生在晶界的应变局部化作用，扩散氢沿晶界移动到应变局部化区域，通过HELP机制促进应变局部化，在与应变局部化带相交的晶界上形成微孔（图 14（c）黑点处）. 微孔聚结并随后沿晶界传播，其作用机制如图14所示[51]. 这种应变局部化现象，即使不存在微孔隙，也会促进裂纹在弹性应变场中的扩展，以及沿晶界的氢局部化.

3.2 氢脆的评价手段和方法

目前，从宏观层面对氢脆的评价手段和研究方法较多. 氢环境的营造方面，可以通过电化学充氢（预充氢、原位充氢、变形后充氢），对研究样品总的氢浓度可以加以控制，但局域氢浓度较难控制. 物理实验中，利用不同变形模式下的恒载荷拉伸（Constant load test, CLT）、线性增强应力拉伸（Linearly increasing stress test, LIST）、恒应变速率拉伸（Constant strain rate testing, CSRT）、慢应变拉伸（Slow strain rate testing, SSRT）等评价断裂应力受加载方式影响明显[1,70]. 对 Fe−17Mn−xC 钢充氢后，通过SSRT单调变形模式和低周期疲劳（Low cycle fatigue, LCF）循环变形模式下抗 HE 性能研究表明：SSRT条件下，由于细小机械孪晶提供了大量的富氢位点，随着C含量的增加，不滑动位错密度增加，由此产生应力集中，也促进了HE，抗HE性能逐渐恶化. 而在LCF条件下，随着C含量的增加，抗HE性能得到改善，这与其在单调变形模式下的行为相反. C含量的增加使层错（Stacking fault，SF）的滑动模式由平面滑动模式变为螺型滑动模式，从而导致富聚氢的分散[71].

利用热解吸谱（Thermal desorption spectroscopy,TDS）可以探究氢与不同类型陷阱的交互作用，但也容易受温度及充氢方式的影响[44]. Motomichi Koyama研究 Fe−Mn−C TWIP 高强钢充氢实验表明，不同的充氢方式，导致钢中的氢扩散量不一样，且塑性损失也有所不同. 变形后充氢最有利于提升钢的氢扩散量，预充氢次之，原位充氢时扩散量最少[38]. 氢脆的影响因素多且复杂，很多实验结果往往趋于片面、笼统，囿于唯象、定性的分析，缺乏全面、精确地表达H在金属中的行为与作用，有时实验数据还相互矛盾，不能自洽. 基于第一性原理和分子动力学（Molecular dynamics, MD）模拟[72−73]，可以从分子、原子层面较准确地表达氢与钢中缺陷的作用行为[74]. 实验方面，可借助氢原子微 印 技 术 (Hydrogen microprint technique, HMT)[75]、三维原子探针（3-dimensional atom probe, 3DAP）等可以对高强钢中氢在晶界、滑移带、夹杂物及析出相被捕捉、分布情况进行直接观察. 通过理论计算、模拟和物理实验相结合的方法，从微观层面较好地揭示氢脆的作用机制.

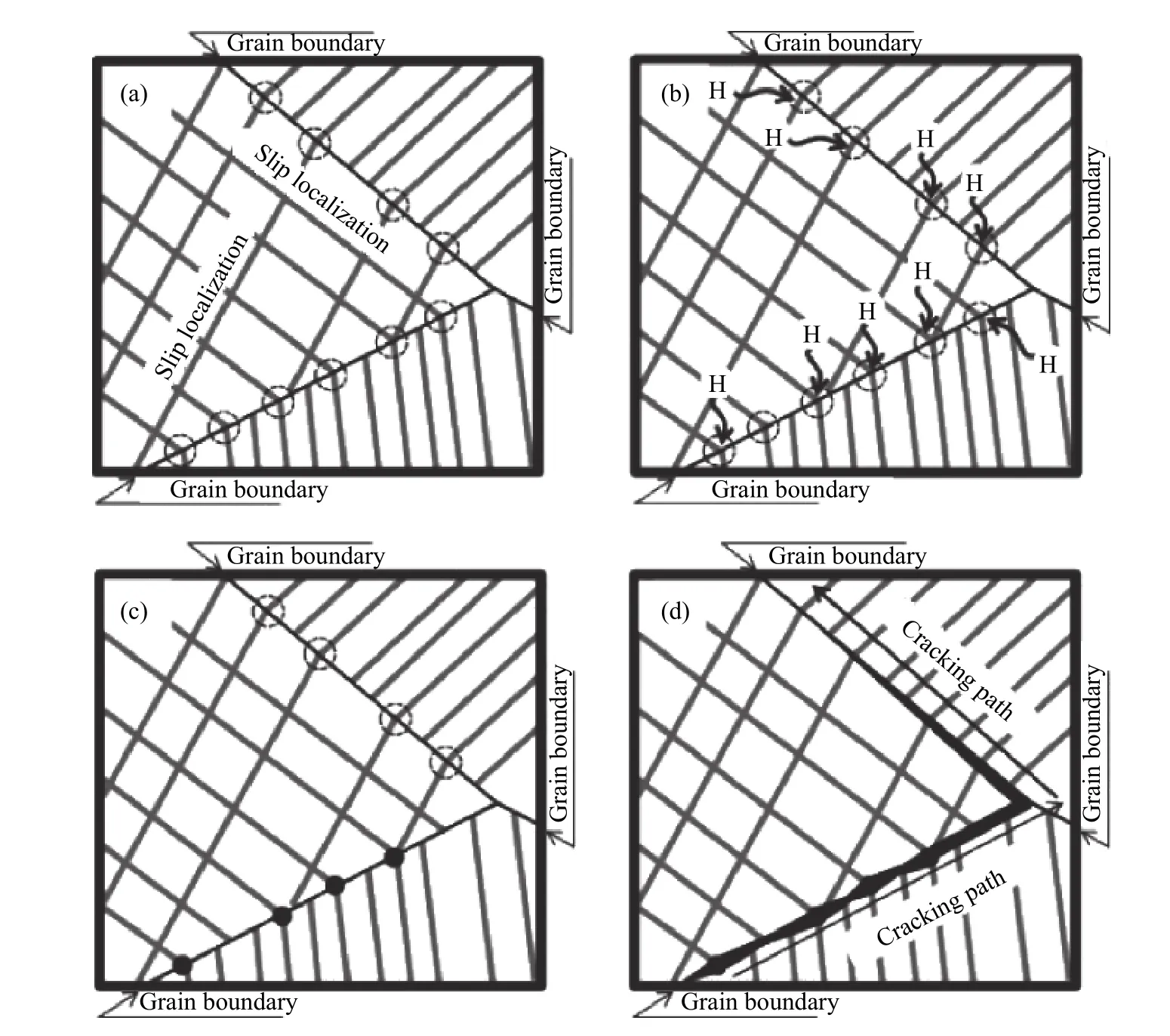
图14 钢中氢辅助裂纹和裂纹扩展的示意图[51]. （a）晶界处应变局部化；（b）扩散氢沿晶界向应变局部化区域迁移；（c）应变局部化带晶界处形成的微空洞；（d）微空洞合并及沿晶界传播Fig.14 Schematic sketches showing hydrogen-assisted cracking and crack propagation in the steel[51]:(a) strain localization occurring particularly on grain boundaries; (b) diffusible hydrogen moving to the strain localization regions along the grain boundaries; (c) formation of micro-voids on the grain boundary intersecting strain localization bands; (d) micro-voids coalescence and subsequent propagation along grain boundaries

4 结束语

随着高强韧性 Fe−Mn−(Al)−C 钢材的应用越来越广泛，材料的显微组织结构越来越复杂多样，面临的HE敏感性越来越突出，高强韧钢材的HE问题必须加以重视. 今后，针对此类高强韧性钢，需要从分子、原子层面研究氢在钢中的作用行为，从微观层面揭示氢脆机制.

（1）高强韧性 Fe−Mn−(Al)−C 钢的组织构成、晶粒形态、大小，以及晶体中空位与溶质原子、位错、层错、孪晶与晶界等缺陷对氢在钢中的行为有重要的影响. 通过对微观组织和晶体缺陷的调控，影响到氢与其交互作用过程中的激活、迁移、结合、氢化物形成的规律，准确地认识氢陷阱的形成、转化规律，有利于深刻地理解相关的科学问题.

（2）基于密度泛函理论的第一性原理计算、分子动力学模拟、氢原子微印技术和三维原子探针的发展对深入研究 Fe−Mn−(Al)−C高强韧性钢中氢原子渗透、溶解和扩散、氢与基体晶格缺陷和析出相的交互作用等方面有重要的帮助.Fe−Mn−(Al)−C钢氢脆的微观作用机制有赖于相关模型的完善和精确计算、表征，这是下一步需要重点关注的研究方向.