基于CNN-LSTM 网络模型的风电功率短期预测研究
2020-09-21彭春华孙惠娟
李 艳,彭春华,傅 裕,孙惠娟
(1.华东交通大学电气与自动化工程学院,江西 南昌330013;2. 国网江西省电力有限公司赣州供电分公司,江西 赣州341000)
目前,风电功率预测方面的研究方法一般可以分为物理模型、统计模型和人工智能三种[1-12]。物理模型是通过物理因素及气象数据来预估风电功率,其在短期预测中表现欠佳。 统计方法是利用基于历史数据的数学模型进行风速、风功率预测,典型统计模型是以风速数据是正态分布且为线性相关为前提的,因不符合实际情况,所以预测性能将不能得以保证。
为改进LSTM 存在的不足,提出一种基于CNN-LSTM 网络模型的风电功率预测方法。借助CNN 序列特征抽象能力以有效提取子序列特征,去除干扰信息后输入数据至LSTM,保留更长的有效记忆信息以解决梯度弥散问题。 与仅使用单一LSTM 模型进行比较,CNN-LSTM 网络模型能提供大量的有效数据作为LSTM的输入数据,从而提高预测精度。
1 风电功率预测影响因素
从物理本质上来说,风电功率影响因素包含风速、风向及温度等[13]。在现有的部分研究中,只使用历史功率数据对未来值进行预测,而不考虑其它相关环境影响因素,此类模型的外推能力不足。 因此,为提升预测的精度,在建立模型时需要考虑其它可能对风电出力造成影响的因素。
存在多个变量时,找出影响预测发电功率较大的变量十分必要。 采用Spearman 方法进行相关性分析。式(1)为2 个n 维向量x,y 的Spearman 相关系数,其中x,y 表示进行相关性分析的两个变量。

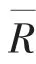
本文实验获取数据包含我国某风电场2018 年的实际测量数据变量,数据采样间隔为15 分钟。 数据包含:测风塔10 m 高度风速、30 m 高度风速、50 m 高度风速、70 m 高度风速和轮毂高度风速、风向、温度、气压、湿度、发电功率。 通过对风电场2018 年风力发电功率与影响因素各变量数据间进行Spearman 相关性计算,分析结果如表1 所示。 风力发电功率与轮毂高度风速具有最强相关性,Spearman 系数达到0.91;同测风塔10 m 风速相关性次之,Spearman 系数是0.90;发电功率与温度相关程度最低为-0.09,所以发电功率与实测数据中的主要影响变量选择为发电功率、测风塔10 m 高度风速、30 m 高度风速、50 m 高度风速、70 m 高度风速和轮毂高度风速。

表1 风力发电功率与影响因子间Spearman 分析结果Tab.1 Results of Spearman analysis between wind power and influence factors
考虑风力发电功率不仅与前一时刻的影响因素有关,在不同时刻下,其影响程度高的因素可能还包含之前几个时刻的风力发电功率及其它影响因子,预测模型输入数据选择为影响发电功率的多个时刻数据值时,其预测准确性就可能比只输入前一时刻数据高。 为此,对表1 中与发电功率影响程度高的影响因子进行分时刻的进一步分析。
对风力发电功率、测风塔10 m 高度风速、30 m 高度风速、50 m 高度风速、70 m 高度风速和轮毂高度风速6 个变量各个时刻数据进行Spearman 相关性分析, 选择出与预测时刻发电功率具有强相关性的某一个或某几个时刻数据,并以此为依据确定分时预测模型的输入数据。 当前风力发电功率与历史风力发电功率部分时刻、发电功率与测风塔10 m 高度风速部分时刻、发电功率与测风塔30 m 高度风速部分时刻、发电功率与测风塔50 m 高度风速部分时刻、发电功率与测风塔70 m 高度风速部分时刻、发电功率与轮毂高度风速部分时刻的相关性分析结果分别如表2~表7 所示。

表2 当前风力发电功率与历史风力发电功率部分时刻Spearman 相关性分析结果Tab.2 Spearman correlation analysis results between current wind power and historical wind power

表3 当前发电功率与测风塔10 m 高度风速部分时刻Spearman 相关性分析结果Tab.3 Spearman correlation analysis results of current generation power and wind speed at the height of 10 m at some time

表4 当前发电功率与测风塔30 m 高度风速部分时刻Spearman 相关性分析结果Tab.4 Spearman correlation analysis results of current generation power and wind speed at the height of 30 m at some time

表5 当前发电功率与测风塔50 m 高度风速部分时刻Spearman 相关性分析结果Tab.5 Spearman correlation analysis results of current generation power and wind speed at the height of 50 m at some time

表6 当前发电功率与测风塔70 m 高度风速部分时刻Spearman 相关性分析结果Tab.6 Spearman correlation analysis results of current generation power and wind speed at the height of 70 m at some time

表7 当前发电功率与轮毂高度风速部分时刻Spearman 相关性分析结果Tab.7 Spearman correlation analysis results of current generation power and wind speed at the height of hub at some time
根据分析情况,选择出与预测时刻发电功率Spearman 相关系数在0.9 以上的时刻数据,并以此为依据确定风电功率网络模型的输入数据。 例如,预测6:45 时刻的发电功率,则输入数据为5:15、5:30、5:45、6:00、6:15、6:30 时刻的发电功率,6:30 时刻的10 m 高度风速,6:30 时刻的30 m 高度风速,6:15、6:30 时刻的50 m高度风速及6:30 时刻的轮毂高度风速。
2 CNN-LSTM 网络模型
2.1 CNN 模型
卷积神经网络源于Hubel 和Wiesel 对于猫脑感受野的探索,是将多层网络结构进行成功训练的学习算法[14]。 CNN 模型通过局部连接及共享权值的方式,交替使用卷积层和池化层以获取数据有效表征。
2.2 LSTM 网络模型
LSTM 的记忆单元结构如图1[15],记忆单元是记忆模块的核心,表示时刻的细胞状态。 LSTM 门结构的作用是增删细胞状态信息,选择性地使信息通过。
各变量之间的计算公式如下
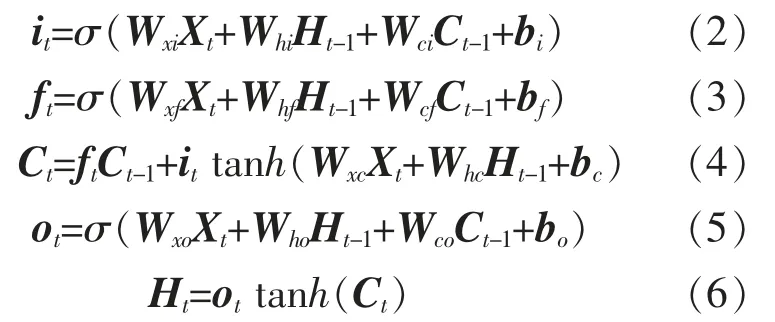
式中:it,ft,ot,Ct分别为输入门、遗忘门、输出门、记忆细胞状态的向量;Wxi,Wxf,Wxc,Wxo为连接输入 信 号Xt的 权 重 矩 阵;Whi,Whf,Whc,Who为 连 接输出信号Ht的权重矩阵;Wci,Wcf,Wco为连接矢量Ct和门函数权重矩阵;bt,bc,bf,bo为偏置向量;σ 为激活函数,通常为或函数。
2.3 CNN-LSTM 网络模型
CNN-LSTM 网络模型的输入数据结构是时间序列特征图。 风力发电功率历史数据、历史时刻风速数据等数据为各自独立的时间序列。 为耦合影响功率的特征信息,将某时刻的历史发电功率和相关的特征表示成向量并联合,成为新的时间序列数据。 如图2 所示,T 时刻的历史功率与相应影响因素耦合构成时刻的特征图,下个时刻的特征图利用滑动窗口的方式滑动一个时间间隔而成。 按顺序把输入的时间序列形成特征图。 n 指时间步数,t 代表特征图以时间为尺度。
CNN-LSTM 网络模型的构成分为两部分,CNN 部分主要进行数据特征提取,LSTM 网络则主要进行功率预测。经实验发现,通过增加CNN层数能够提高提取特征的能力, 模型精度会变得更高,但是当增加到一定层数之后,模型的拟合精度趋向稳定, 因此最后将卷积层(Conv2D)数定为4。 卷积层通过将特征映射到池化层(Maxpooling2D),减少了输出维数,实现特征提取。然后使用Flatten 层进行扁平化操作,再采用全连接层(Dense)输出向量,即归一化后的风电功率预测结果。

图1 LSTM 单元结构Fig.1 LSTM unit
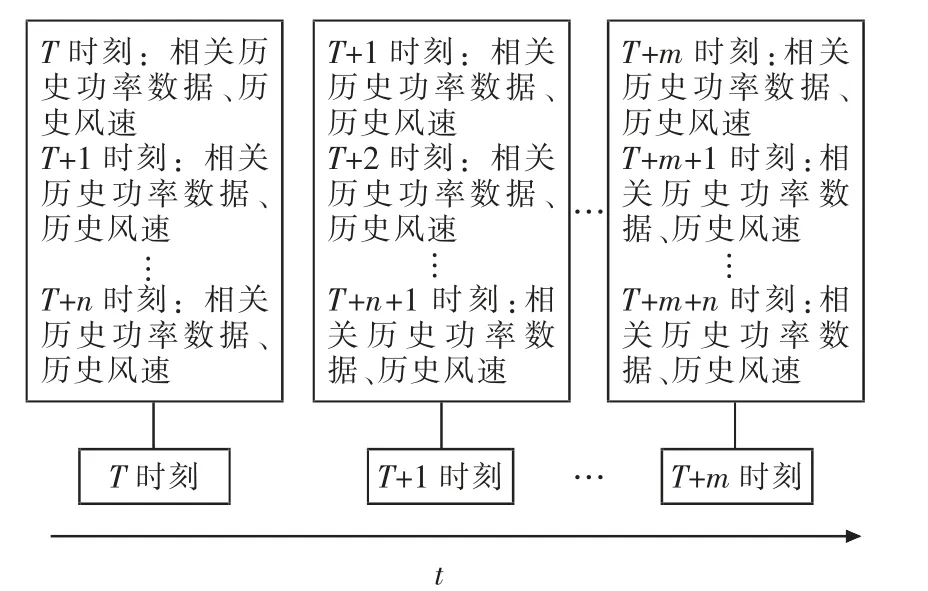
图2 CNN-LSTM 网络模型输入数据结构Fig.2 Structure of input data in CNN-LSTM network model
3 算例分析
3.1 实验评价指标
评估模型预测值与训练值拟合程度采用均方误差(MSE)作为损失函数,若损失函数值越小,说明模型拟合的越好,则预测更精确。计算公式为式(7)。以平均绝对误差(MAE)为指标对预测结果的进行评价,计算公式为式(8)。

式中:N 为样本个数;pi为发电功率预测值;Pi为发电功率实际值。
3.2 实验结果分析
采用国内某风电场2018 年4 月6 日至2018 年4 月10 日采集的数据进行实验,分别应用BP、LSTM 和CNN-LSTM 预测发电功率,可得到如图3 所示的预测结果对比曲线,以及图4 所示的对应各时刻的相对误差情况。 可见CNN-LSTM 的预测结果与实际值最接近。
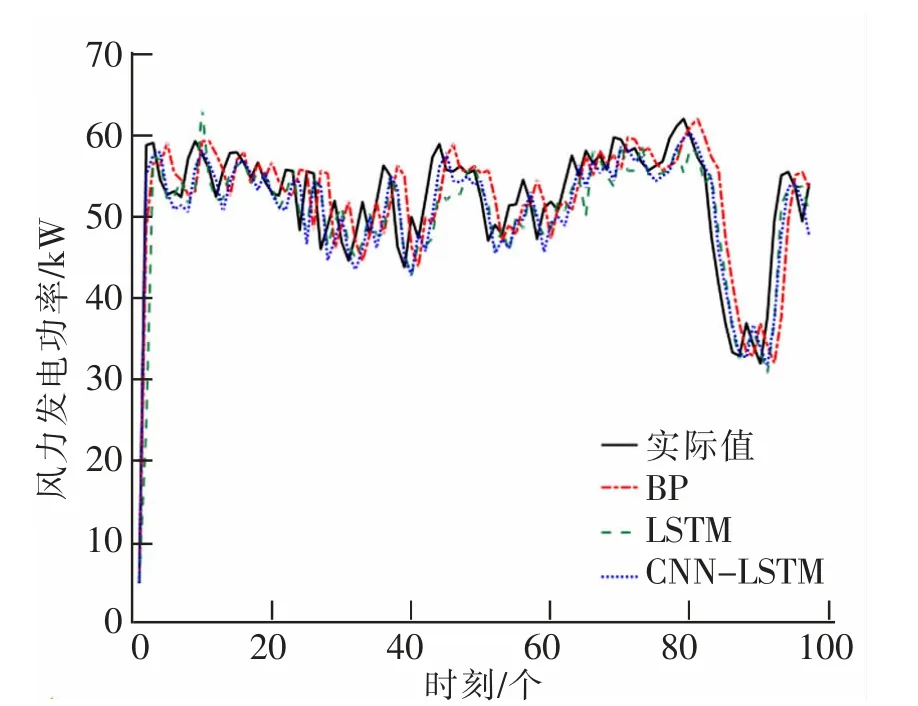
图3 4 月9 日预测结果对比图Fig.3 Comparison chart of forecast results on April 9th

图4 4 月9 日预测相对误差曲线Fig.4 The relative error curveof prediction on April 9th

表8 预测结果误差对比Tab.8 Error comparison of prediction results
从表8 可看出,本文提出的CNN-LSTM 预测方法得到风电场2018 年4 月6 日至2018 年4 月10 日期间的eMAE明显小于BP 和LSTM 网络模型得到的eMAE,说明利用CNN-LSTM 模型可提高预测精度。
4 结论
针对提升预测精度的要求,本文提出一种基于CNN-LSTM 网络的风电功率预测方法,并经过实验验证了其有效性。 算例表明:
1) 采用Spearman 分析不同变量间的相关性,可以对预测模型的多变量输入进行筛选,从而降低数据规模,减少非有效信息给模型精度带来的影响。
2) 基于CNN-LSTM 网络构建的预测模型, 不仅具有CNN 适于提取数据特征的优点, 又包含了LSTM处理时间序列的能力,实验结果验证文中预测方法能够提高风电功率的预测精度。
当风力发电功率出现持续性突变时,深度学习算法的跟踪性能需进一步加强。 下一步的研究可结合优化算法来提升其预测效果。
