水轮发电机组阻尼绕组连接片的包辛格效应

2020-09-21李金泽谢克非

华东交通大学学报 2020年4期

李金泽，谢克非

（南昌工程学院机械与电气工程学院，江西南昌330099）

水轮发电机阻尼绕组主要是防止发电机在负载突变时对发电机绕组的冲击。发电机在负载变化时，其绕组内的电压和电流会形成一个震荡的过程。发电机阻尼绕组（紫铜材质）固定在磁极上受拉，运行一段时间后受热膨胀后相互挤压，常出现烧伤、因拉压导致强度损毁等现象[1-6]。

因此，国内外对解决水轮发电机组阻尼绕组失效的研究一直持续不断，2019 年陈国强[1]对阻尼绕组阻尼条的故障进行了分析与探讨，结合宁钢近年来出现的几起同步电动机故障处理经验,对阻尼条断裂后探索了一种新型处理方法；Bauw G 对带有阻尼绕组的发电机组的噪声及振动问题进行了研究[8]。阻尼绕组问题根本原因在于内部拉压应力的变化，导致材料发生形变。

对阻尼绕组拉压过程进行包辛格效应（Bauschinger Effect，BE）研究，有利于解决阻尼绕组出现的工程问题。阻尼绕组结构包括阻尼铜条、阻尼铜环、磁极、阻尼条和铜环的连接件阻尼连接片构成，见图1，整个结构中，阻尼绕组中阻尼连接片拉压应力最为明显。

图1 阻尼绕组结构Fig.1 Damping winding structure

1 试样制备及实验方法

1.1 试样制备

试验用阻尼绕组连接片为紫铜材质，其中加入少量脱氧元素或其他元素以改善材质和性能,也可称之为紫铜合金。阻尼绕组连接片紫铜合金[9-11]，化学成分为：Cu+Ag 99.90%，Bi 0.001%，Sb 0.004%，As 0.005%，Fe 0.001%，Pb 0.005%，S 0.001 5%，O 0.000 5%。

紫铜试样按国标GBT 26077-2010 金属材料-疲劳试验-轴向应变控制方法加工, 将尺寸为120 mm×120 mm×20 mm 的原材料分割成5 份试样，每份试样的表面磨去0.4～0.5 mm ,以消除表面状态的影响。 BE轴向加载试样如图2 所示，总长度为120 mm，直径为15 mm，中间加载部位长度为20 mm，直径为6 mm。在离最终尺寸还差0.1 mm 时，以每道工序不超过0.005 mm 速度进行研磨，研磨后对试样表面再沿试样轴向进行抛光处理。

图2 试样加工尺寸规格（单位：mm）Fig.2 Processing dimensions and specifications of samples（Unit：mm）

1.2 实验方法

安排5 组试验。其中一个试样进行单向拉伸试验,测量金属拉伸强度，作为紫铜“原始拉伸强度”，其余4个试验分别进行不同预压缩变形后的拉伸试验，测量拉伸屈服强度。试验在电液伺服疲劳试验机（INSTRON 8801）上进行[12-13]，拉伸速率为0.5 mm/min，压缩速率为0.2 mm/min，试验温度为室温。以固定速率（0.2 mm/min）进行4 组压缩试验，分别按1.0%，2.0%，3.0%，4.0%的压缩形变量进行，记录4 组实验的压缩荷载值，以固定速率（0.5 mm/min）进行4 组拉伸试验，拉伸形变量为3%，4 组为上述压缩后试样，记录4 组试验的拉伸荷载值。以固定速率（0.5 mm/min）进行1 组拉伸试验，拉至试样失效，记录实验的拉伸载荷值。

2 试验过程

2.1 压缩试验

对加工好的5 个试样，任取4 个，编号分别为1#，2#，3#，4#，以0.2 mm/min 的速率进行压缩试验，1#试样进行压缩1%（2 mm）的形变量，2#试样压缩2%（4 mm）的形变量，3#试样压缩3%（6 mm）的形变量，4#试样进行压缩4%（8 mm）的形变量。提取部分试验数据绘制成表1 及表2。表1 左表为1#试样压缩试验数据，右表为2#试样压缩试验数据；表2 中左表为3# 试样压缩试验数据，右表为4#试样压缩试验数据。

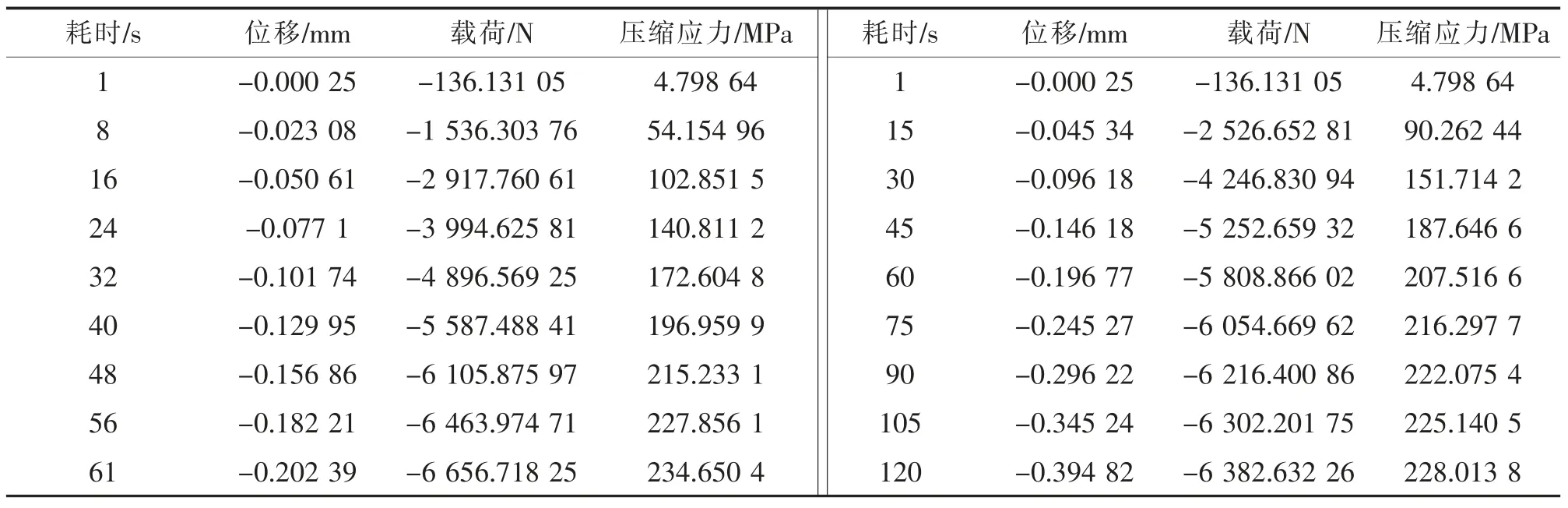
表1 1#和2#试样压缩Tab.1 Sample1#and 2#compression

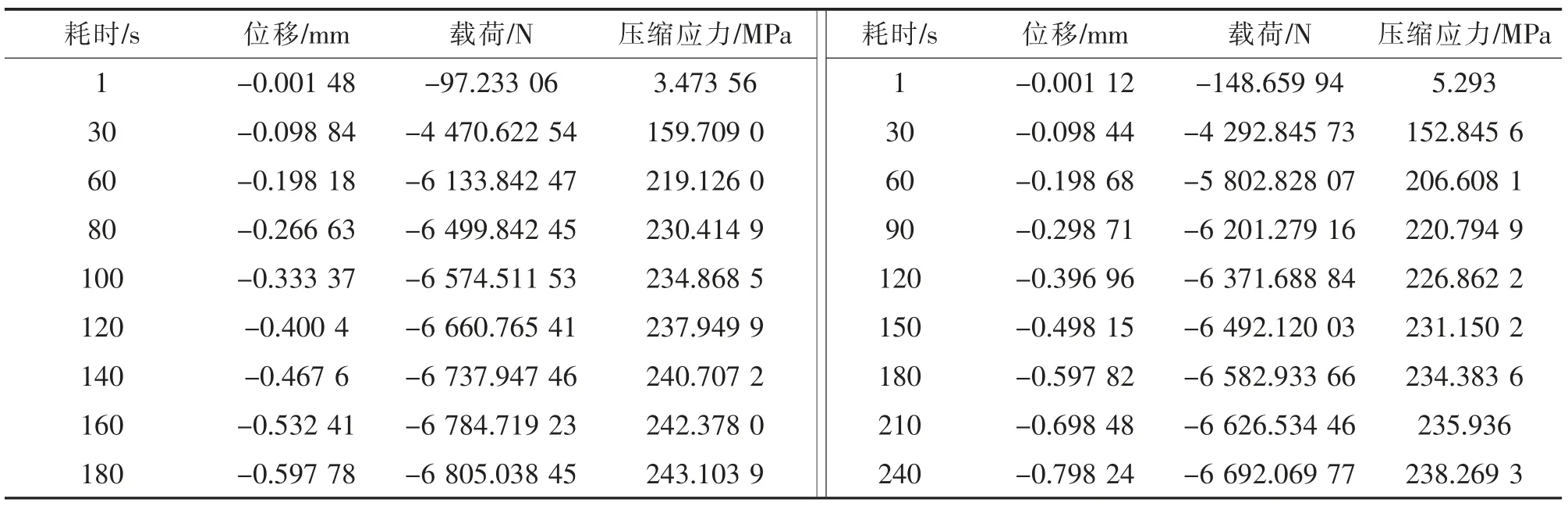
表2 3#和4#试样压缩Tab.2 Compression of Sample 3#and 4#

通过表1 及表2 可以看出，耗时为30 s 时，2#试样的载荷为4 546 N，压缩应力为151 MPa，3#试样的载荷为4 470 N，压缩应力为159 MPa，4#试样的载荷为4 292 N,压缩应力为152 MPa。在不同压缩应变实验下，同时间段的载荷值与压缩应力值基本相同。

1#试样在压缩1%（2 mm）时，荷载值为6 656 N，压缩应力为234 MPa；2#试样在压缩2%（4 mm）时，荷载值为6 382 N，压缩应力为228 MPa；3#试样在压缩3%（6 mm）时，荷载值为6 805 N，压缩应力为243 MPa；4#试样在压缩4%（8 mm）时，荷载值为6 692 N，压缩应力为238 MPa。不同压缩应变试验下，在达到最终压缩形变量时，不同试验的施压荷载值，压缩应力值相差不同，形变量的最终大小与荷载值、压缩应力无明显相关性。

将4 组压缩试验数据绘制成图，如图3 所示。横坐标表示压缩变量，从1%（2 mm）增加到4%（8 mm）,纵坐标为压缩载荷值，以kN 为单位。从图中可以看出，水轮发电机组阻尼绕组紫铜连接片的载荷/应变曲线基本都处于相同的变化趋势，但也有细微的不同，1#，2#和3#试样的变化趋势基本一致，最终荷载值趋向于6 500 N 左右，但4#试样在最终形变时，载荷需求增大，随着压缩形变量的激增，4#试样的载荷需求增大明显。

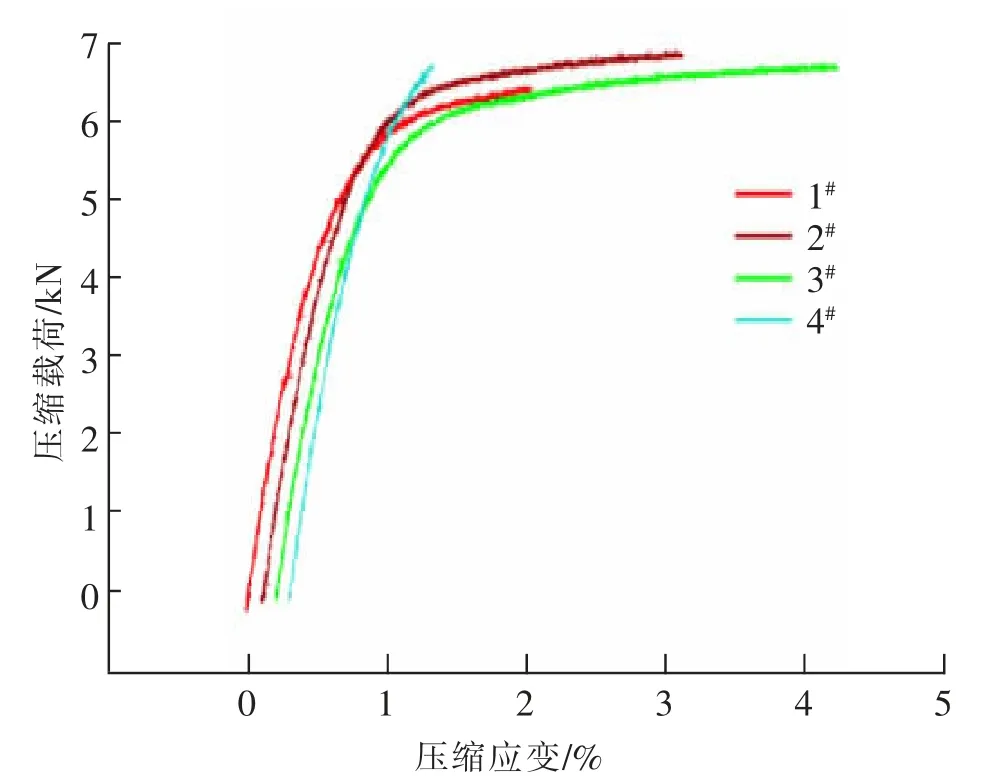
图3 紫铜连接片压缩试验Fig.3 Compression test of copper joint

2.2 拉伸试验

取未压缩的试样，及上述压缩后的4 个试样，进行拉伸试验，编号分别为1′，2′，3′，4′，5′，以0.5 mm/min 的速率进行拉伸试验，1′试样为原始拉伸试样，拉伸至丧失屈服强度，可截取任意段作为对比数据，其余4 个试样拉伸量均为3%（6 mm）；2′试样为压缩1%（2 mm）的形变量下拉伸试验，3′试样为压缩2%（4 mm）的形变量下拉伸试验，4′试样为压缩3%（6 mm）的形变量下拉伸实验，5′试样为压缩4%（8 mm）的形变量下拉伸实验。提取部分试验数据绘制成表3，表4。表3 左表为2′试样拉伸试验数据，右表为3′试样拉伸试验数据；表4 中左表为4′试样拉伸试验数据，右表为5′试样拉伸试验数据。

从表3 及表4 中可以看出，开始拉伸（1 s）时，3′试样的起始载荷为369 N，2′，4′和5′试样的起始载荷都在500～550 N 之间，3′试样的起始载荷远远小于其他的3 个试样，表明3′试样的初始拉伸试样的需求载荷（力）最小，在几个试样试验中荷载处于极小值。随着耗时、拉伸量的增加，最终拉伸量为3%（6 mm）时，2′试样的最终载荷为6 230 N,拉伸应力值为225 MPa；3′试样的最终载荷为6 609 N，拉伸应力为225 MPa；4′试样的最终载荷为6 383 N，拉伸应力为227 MPa；5′试样的最终载荷为7 413 N，拉伸应力为261 MPa。在拉伸量终值时，3′试样的载荷值远远大于2′和4′试样，在前3 组试样中，处于荷载极大值。

表3 2′和3′试样压缩Tab.3 Compression of Specimen 2′and 3′

表4 4′和5′试样压缩Tab.4 Sample4 'and 5' compression

将1′试样，进行拉伸试验，拉伸至试样失去屈服强度，提取部分数据绘制成表5。在表5 中可以看出，初始拉伸（1s）时，试样1′的初始荷载为502 N，拉伸应力为19 MPa，随着耗时、拉伸量的增加，在拉伸量为3%（6 mm）时，试样1′的载荷为6 283 N，拉伸应力为238 MPa。

将试样1′，2′，3′，4′，5′的拉伸试验数据绘制成图，如图4 所示。在图4 中可以看出，试样2′，3′，4′，5′经过压缩试验后，再进行拉伸试样，最终曲线趋向荷载值均小于试样1′的曲线趋向荷载值。说明，包辛格效应在水轮发电机组阻尼绕组紫铜连接片中存在明显。

在2′，3′，4′组试样曲线中可以看出，3′试样在其中属于极值，最终拉伸应力值远高于2′试样和4′试样。但5′试样最终拉伸应力值远超于2′，3′，4′组试样，并且也远超于试样1′的最终拉伸应力，试样5′的现象说明，水轮发电机组阻尼绕组紫铜连接片的包辛格效应在压缩量4%（8 mm）以下再拉伸时，现象明显，超过压缩量4%（8 mm）再拉伸时，包辛格效应不再突出。

此外，通过试样1′的完全拉伸试验可以看出，阻尼绕组连接片的最终拉伸应力值趋近于240 N 左右，不在发生明显变化，阻尼绕组连接片的最终拉伸应变量值在43%左右时，材料发生断裂，彻底损毁，进一步验证了阻尼绕组紫铜连接片的伸长率在45%左右的物性参数。