双幅桁架组合梁空间受力研究

戴文蓉，陈建兵，周 晨

（1.苏州科技大学土木工程学院，江苏 苏州215011；2.中交一公局第二工程有限公司，江苏 苏州215011）

空间管桁架组合梁是以一般钢-混凝土组合梁为基础发展而来的新型组合结构， 将管桁架和混凝土板通过剪力键连接在一起协同工作、共同受力。 双幅桁架组合梁则是通过横向联结系将两幅相同的管桁架组合梁连接在一起。 目前位于四川境内的干海子特大桥就是世界上最长的双幅钢管桁架梁公路桥，由混凝土翼板与管桁架组成的新型结构能够更加充分地发挥钢材和混凝土各自的材料性能，整体性强、空间刚度大、结构截面尺寸小、受力合理、承载能力高、抗震性能和动力性能优越、施工方便等优点[1-2]。

目前已有学者针对单幅钢管混凝土桁架组合梁进行相应试验研究，重点主要包括两个方面：①组合梁的桁架节点承载能力及疲劳性能，例如刘永健等[3]通过对T，Y 形两种桁架节点以及钢管内是否灌注混凝土进行试验研究，得出了节点承载力计算时需要考虑不同的破坏形式。 ②组合梁整体受力性能，例如姜如[4]以干海子大桥为参考依据，研究了其结构自振特性，归纳总结了此类桥的静动力学行为的一般规律；潘年等[5]通过试验实测在结构力学的基础上提出了桁架组合梁的挠度、短期刚度及抗弯承载力计算公式等。 但是在诸多空间桁架组合梁试验分析中关于双幅桁架组合梁受力性能的研究成果却很少，国内外涉及该类型组合结构规范中也没有详细的设计理论和计算公式，仅少数文献有相关结构的介绍及分析，但也只是借助于有限元软件的简单模拟分析，对于该结构的受力性能的试验分析几乎没有，模拟与试验结果不能得到验证；因此有必要进一步针对该新型结构进行受力性能试验研究，且实际工程中双幅桁架组合梁桥对于中等跨径与大跨径的桥梁结构更具有竞争力，有较好的工程应用前景。

通过对双幅桁架组合梁进行试验研究，分析该组合梁在单幅对称加载情况下的受力性能，并且与ABAQUS有限元软件后处理结果比较，结合试验实测与模型数据分析试件在单幅对称加载作用下的位移、沿截面高度纵向应变、混凝土板顶纵向应变、斜腹杆轴向应变以及横向联结系轴向应变随荷载的发展变化和分布规律。

1 试验概况

1.1 试件设计

试验梁尺寸拟参照某钢管混凝土桁架组合连续梁实桥，试验梁的长宽高按实桥1/10 的相似比进行设计，各腹杆外径也是采用实桥1/10 的相似比拟定，缩尺模型以后的双幅桁架组合梁全长2 100 mm，宽2 000 mm，计算跨径1 880 mm，其中单幅混凝土板宽900 mm，厚95 mm，单幅管桁架中，管桁架的轴心高270 mm，上弦杆之间轴心距离450 mm，试件几何尺寸如图1 所示。

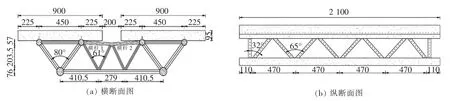
图1 双幅桁架组合梁几何尺寸图（单位：mm）Fig.1 Geometrical dimensions of double-span truss composite beams （Unit： mm）

混凝土板采用C40，板内双层配筋，纵筋与横向箍筋均是φ8@100。 在管桁架上焊接抗剪刚度较大，强度较高及抗疲劳能力较强的开孔钢板新型剪力键[6-7]，可以减小混凝土板与桁架交界处滑移效应对试件的影响，每片剪力键长160 mm、宽30 mm、厚3 mm，钢片上钻2 个直径12 mm 的孔，2 个孔距离120 mm，箍筋穿过开孔连接件，让混凝土板与管桁架的连接更牢固。

双幅管桁架的上下弦杆、斜腹杆以及拉杆均采用Q345 级热轧无缝圆钢管，上弦杆型号为D57×3，下弦杆型号为D76×3，腹杆型号为D32×3，拉杆型号为D26×3，腹杆与弦杆的节点连接处采用直接焊接。 沿组合梁横向，斜腹杆之间的角度是80°；沿组合梁纵向，其中直腹杆与斜腹杆夹角是32°，斜腹杆之间角度是65°，各个斜腹杆相邻节点距离470 mm。因为加载组合梁时支座处会产生集中力，所以上下弦杆中均灌入强度为C60 的混凝土砂浆，可以避免弦杆受压内凹和局部屈服[8]。

横向联结系是由横斜腹杆、横杆以及横向连接下弦杆组成，型号分别是D20×3，D26×3，D34×3。沿组合梁横向，横斜腹杆之间的角度是61°，沿组合梁纵向，横斜腹杆之间的角度是65°。 横向联结系中的横杆与上弦杆焊接时， 沿组合梁的竖直方向往下偏14 mm， 避免加载时混凝土板下压触碰到横向联结系导致杆件受力。

1.2 材性试验

按照《混凝土结构设计规范》[9]的相关要求，制作试验梁的同时浇筑尺寸为150 mm×150 mm×150 mm 的标准立方体试块， 按规定养护并得到C40 混凝土的平均抗压强度为37.66 MPa， 轴心抗压强度标准值为25.19 MPa，弹性模量为3.20×104 MPa。 钢材的屈服强度fy、抗拉强度fu和弹性模量E 如表1 所示。

表1 钢材力学性能Tab.1 Mechanical properties of steel

1.3 加载方案

试验梁加载装置主要包括2 个500 kN 的手动液压千斤顶、压力传感器、WH-1000 型荷载仪等。 在支座处垫上圆柱形钢棒来模拟竖向铰接约束。 试验采用2 个液压千斤顶同步加载，两个加载点位于A 幅跨中位置上弦杆正上方。在试验开始前，试件需要通过预加载来消除试件与加载装置之间的缝隙，并且检查测试仪器能否正常工作。

1.4 测点布置

用DH3821Net 静态应变测试系统对混凝土板上单向应变片以及管桁架应变片的数据进行采集。 试验梁竖向变形采用量程为±100 mm 位移计测量。

为了得到混凝土翼缘板各截面纵向应变，在L/4，3L/8，L/2 三个测试截面顶部及底部各均匀布置11 个混凝土应变片； 为了得到双幅桁架组合梁在荷载作用下的挠度，在跨中截面的下弦杆以及混凝土板处都布置了位移计， 表2 为各个位移计编号；为了得到管桁架腹杆的轴向应变，在各个测试腹杆沿轴线4 个方向都贴上应变片；为了得到加载时双幅桁架组合梁的横向联结系的受力状态，横斜腹杆四周以及节点位置处都需要布置应变片。

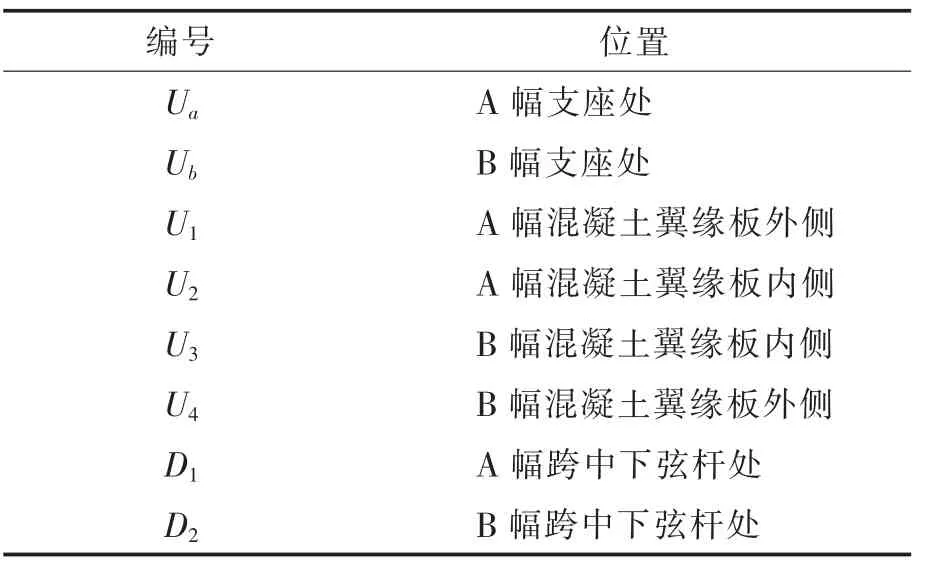
表2 位移计编号Tab.2 Displacement gauge number

2 试验结果及分析

2.1 试件现象及结果

以20 kN 为一个荷载等级在试件的A 幅施加双点对称集中力，①加载初期，因为施加荷载值较小，通过开孔剪力键连接在一起的混凝土板与管桁架协同工作、共同受力，表现出双幅桁架组合梁在弹性阶段良好的工作性能；②当P=100 kN 时，试验梁的A 幅混凝土板和下弦杆开始出现明显下挠，而B 幅混凝土板外侧则轻微上翘；③当P=200 kN 时，混凝土板底以及板侧可以观察到细小裂缝，此后荷载增加速度远远小于跨中挠度的增长速度，表明试件开始进入弹塑性状态；④当P=240 kN 时，A 幅混凝土板顶加载点附近有明显横向裂缝，随着荷载的增长，其翼板裂缝宽度、长度也在进一步扩展，同时可以观察到A 幅梁斜腹杆中受压杆出现明显弯曲，横向联结系中压杆也出现明显的弯曲；⑤最后当P=260 kN 时，混凝土翼板顶板横向裂缝变大、顶板压碎，同时伴随着一声巨响，A 幅的下弦杆与斜腹杆的焊接处断裂，试件加载破坏。 A 幅的斜腹杆与弦杆之间发生冲剪破坏，所以试件是由于斜腹杆和上下弦杆之间断裂而提前退出工作，试验以节点的拉断终止，其中焊接工艺的好坏是试件加载破坏的主要原因。

2.2 荷载-挠度曲线

图2 为双幅组合梁单幅对称加载作用下A幅跨中截面下弦杆底部荷载-挠度关系曲线，观察可知挠度曲线变化特征体现了试验梁在整个加载过程中经历了弹性、弹塑性以及破坏3 个阶段。 由挠度的发展趋势可知，当P＜200 kN 时，挠度随荷载增加呈线性发展，弹性阶段时双幅桁架组合梁具有良好的整体工作性能； 当P=240 kN时， 试验梁的挠度增长速率大于荷载的增长速率； 直至P=260 kN 时，A 幅梁发生弯曲破坏，同时斜腹杆与上下弦杆连接处断裂，所以试验梁整体的抗弯极限承载力为260 kN。

图2 双幅桁架组合梁荷载挠度曲线Fig.2 Load deflection curve of double-span truss composite beam

图3 为试验梁沿宽度方向挠度的变化曲线，可以看出双幅桁架组合梁在屈服前即荷载还未达到200 kN 时， 加载点所在A 幅梁的跨中挠度从中点处向两边逐渐减小， 随着荷载的增加，其挠度变形的增量也不断增加。由图可以观察到虽然加载点位于A 幅梁， 但是B 幅梁跨中挠度也有较小幅度的变化，由于横向联结系的作用B 幅混凝土板内侧也有向下挠度，而B 幅混凝土板外侧有反向位移，位移变化在1 mm 左右，B 幅跨中下弦杆的位移接近0，所以单侧加载时另一幅梁受力影响小且未发生倾覆情况，该双幅桁架组合梁稳定性较强。

图3 沿梁宽各点挠度曲线Fig.3 Deflection curves at various points along the width of the beam

2.3 组合梁沿截面高度纵向应变分布

双幅桁架组合梁跨中沿截面高度纵向应变分布如图4 所示， ①当组合梁处于弹性工作状态时，混凝土板与管桁架连接处未出现滑移，随着荷载增加，交界面处滑移效应明显；②下弦杆处出现拐点应该是下弦杆同时承受受拉和受弯的内力所导致的； ③图中虚线表示忽略上弦杆与混凝土板的滑移效应以及下弦杆的内力作用则纵向应变沿梁高近似呈线性分布， 所以组合梁纵向应变沿跨中截面高度分布基本符合平截面假定；④当加载到80%极限荷载时，虚线斜率逐渐减小， 且中和轴也随着荷载增加逐步上移，表明跨中混凝土板底发生明显开裂，从而退出工作。

图4 组合梁沿截面高度纵向应变发展Fig.4 Longitudinal strain development of composite beams along the section height

2.4 剪力滞效应分析

单幅加载作用下的组合梁混凝土板沿板宽方向的纵向应变分布有较大的差异， 出现了剪力滞后的现象[10]。 如图5 所示，混凝土板板顶应变横向分布的变化幅度随着荷载的增加而离散程度越大，并且呈现出混凝土板与管桁架交界处应变值达到最大， 向翼板两侧逐渐减小的现象。剪力滞效应较为明显。 由此可见，单幅加载作用下双幅桁架组合梁跨中截面沿纵向的最危险（不利）截面在混凝土板与管桁架交界处。 所以在实际工程中， 我们对双幅桁架组合梁进行设计时，不能忽略单幅加载时组合梁的剪力滞效应。

将各测点纵向应变换算成相应的剪力滞系数，并且绘制剪力滞系数沿组合梁横向分布图，如图6 所示。 当P=220 kN 时，其梁肋处剪力滞系数λ 分别为1.21，1.42，梁肋处系数达到峰值，向两边逐渐减小，并在跨中截面的中心位置处达到最小。 随着荷载的增加，曲线的离散程度也逐渐增大，但是变化趋势相同，梁肋处剪力滞系数越大，表示该处的应力分布越不均匀。

图5 混凝土顶板应变分布Fig.5 Strain distribution of concrete roof

当A 幅施加一对集中荷载时，探讨剪力滞效应沿组合梁纵向的分布规律，整个组合梁的计算跨径为1 880 mm，纵向的参考点分别设置在1/4 截面（525，1 575 mm），3/8 截面（787.5，1 312.5 mm）以及跨中截面处（1 050 mm），共5 个参考点，当P=100 kN 和P=200 kN 时，计算出该5 个参考点的剪力滞系数，同时绘制出剪力滞系数沿桥梁纵向的分布曲线如图7 所示。 由图可知，当荷载为100 kN，整个组合梁处于弹性阶段时，剪力滞系数的影响范围在787.5～1 312.5 mm，而且以跨中为对称轴变化。 当荷载为200 kN 时，试件进入屈服阶段，此时对比弹性工作状态，可以明显发现剪力滞效应的影响范围扩大，影响范围在656.25～1 443.75 mm，可知随着荷载的增大，加载点截面处的应力分布不均匀性也在逐渐扩大。 弹性阶段下剪力滞效应沿桥纵向的影响范围很小，主要集中在加载点的位置，而组合梁开始屈服时，剪力滞效应的影响范围扩大，主要由集中力作用处向两边发展，且剪力滞系数峰值也比弹性阶段时有所增加，200 kN 时剪力滞系数曲线可以观察到两边出现拐点突变，主要是加载后期产生明显的端部滑移，且后期变形集中于中间区域[11]。

图6 剪力滞系数横向分布Fig.6 Lateral distribution of shear lag coefficient

图7 剪力滞系数纵向分布Fig.7 Longitudinal distribution of shear lag coefficient

2.5 组合梁腹杆轴向应变

双幅桁架组合梁中A 幅腹杆的编号如图8所示，同时绘制出A 幅各腹杆的荷载平均轴应变曲线如图9、图10 所示。 B 幅梁跨中斜腹杆9 和斜腹杆10 的荷载平均轴应变如图11 所示。

斜腹杆1，3，5，7 为压杆，斜腹杆2，4，6，8 为拉杆，各个压杆的变化趋势一致，且同等荷载作用下对应的应变大小相近，偏差较小。 而各个拉杆之间的偏差较大，表现为同等荷载作用下，支座处的拉杆比跨中处的拉杆应变值变化大。当P＜200 kN 时，荷载-轴应变的关系曲线都呈线性发展，当加载至90%极限荷载，拉杆的应变值均小于压杆的应变值，从之前的破坏特征来看，拉断的是斜腹杆2 和斜腹杆6，这两根拉杆的拉应变值达到屈服值， 即1/8 截面处斜腹杆6 与上弦杆节点破坏以及1/4 截面处斜腹杆2 与下弦杆节点破坏。

图8 A 幅腹杆编号Fig.8 Number of A-frame abdominal rods

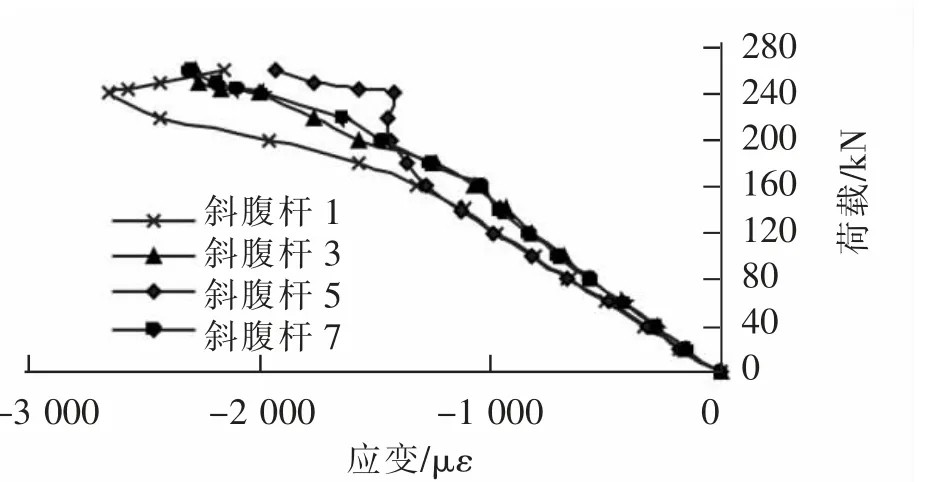
图9 压杆荷载平均轴应变Fig.9 Average axial strain of load on compression bar

图10 拉杆荷载平均轴应变Fig.10 Mean axial strain of tie rod load

图11 B 幅跨中腹杆荷载平均轴应变Fig.11 Mean axial strain of mid-span beam load in B-frame

2.6 组合梁横向联结系腹杆荷载轴应变分析

试件极限加载破坏后，分析单幅加载作用下横向联结系的受力状态，分别对支座处以及跨中处的横向联结系进行编号，如图12 所示，并绘制各腹杆荷载轴应变分布图，如图13，14 所示。

1） 支座处横向联结系， 横斜腹杆1，3 是拉杆，横斜腹杆2，4 是压杆，该4 根横斜腹杆的变化规律相同，在荷载达到200 kN 之前，整个横斜腹杆的荷载应变呈线性发展，之后随着荷载的增加， 应变的增长幅度远大于荷载的增长幅度，但是横斜腹杆并没有达到屈服强度，并且发现，在同等荷载作用下，靠近A 幅梁一侧的横斜腹杆1，2 的应变绝对值要大于靠近B 幅梁一侧的横斜腹杆3，4 的应变绝对值。 再对比横斜腹杆1，2 以及横斜腹杆3，4，发现对应位置处横斜腹杆的拉应变与压应变绝对值的相差不大。

图12 横向联结系编号Fig.12 Number of horizontal connections

图13 支座处横斜腹杆荷载轴向应变Fig.13 Axial strain of the transverse web at the bearing

图14 跨中处横斜腹杆荷载轴向应变Fig.14 Axial strain of transverse web member under mid-span load

2） 跨中处横向联结系，横斜腹杆6，8 是拉杆，横斜腹杆5，7 是压杆，在弹性工作状态下，应变随荷载增加都呈线性发展，与支座处横向联结系的变化规律相同即靠近A 幅一侧的横斜腹杆的应变绝对值大于另一侧腹杆应变绝对值，但位于同一侧的拉压杆应变绝对值相近，对比支座与跨中位置的横向联结系，支座横斜腹杆轴力均小于跨中横斜腹杆轴力。

3 结论

1） 双幅桁架组合梁在单幅对称加载作用下破坏形态表现为A 幅弯曲破坏， 同时伴随着受拉腹杆节点位置的冲剪破坏，B 幅仅斜腹杆受轴力且影响较小，所以确保节点的焊接质量是工程中不可或缺的一步。

2） 组合梁试验结果表明，当P＜200 kN 时组合梁处于弹性状态，试件屈服后塑性区域不断向上发展，内力重新分布，中性轴上移。 组合梁刚度下降，位移增加速率比弹性阶段快，非线性特征明显。

3） 剪力滞系数沿横向分布规律为梁肋处的剪力滞系数达到峰值，且由此向两边逐渐减小，说明梁肋处应力分布最不均匀；在单幅跨中施加一对集中荷载，剪力滞效应沿组合梁纵向的影响范围很小，主要分布在加载点附近，加载后期曲线出现拐点突变是因为加载后期产生明显的端部滑移，而变形集中于中间区域。

4） 单幅对称加载，组合梁的弦杆、斜腹杆以及横向联结系中横斜腹杆主要承受轴向力，而弯曲效应影响较小，但是下弦杆处弯曲效应对杆件的受力影响较大，不容忽视。