Maxwell 方程特征值问题的谱方法

陈亚飞，茆晋晋

（1. 淮北师范大学数学科学学院,安徽 淮北235000 ；2. 中国矿业大学数学学院,江苏 徐州221116）

谱方法起源于经典的Ritz-Galerkin 方法，是一种数值求解偏微分方程的方法：谱方法最大的优点是具有“无穷阶”收敛性及可采用快速算法，现已被广泛用于气象、物理、力学等诸多领域，成为继差分法和有限元法之后又一种重要的数值方法。 2015 年，樊占玲[1]将两类线性基本问题的谱方法基础上，分别构造出一维、 二维非线性Sine-Gordon 方程的半离散与全离散格式， 最后用数值模拟验证了该方法的有效性。 2016年，刘文杰[2]应用Chebyshev－Galerkin 谱方法离散一维半线性抛物方程的空间变量，然后使用谱配置法或块谱配置法离散时间变量，得到了在L2权范数下的空间半离散格式的最优阶误差估计结果。2017 年，刘贺[3]用谱方法来研究一类一维空间周期型的Cahn-Hilliard 方程并证明了其收敛性。 2018 年，董帅等[4]对非线性项用Legendre 插值，在空间上用Legendre-Galerkin-Chebyshev 方法，在时间上用二阶Crank-Nicolson 格式，提出Burgers 方程的广义多项式混沌-谱方法将Burgers 方程转化为非线性微分方程组。 基于以上各种间断Galerkin 算子的谱性质，本文考虑真空中电磁场的Maxwell 方程问题形如下[5]

对于三维Maxwell 方程[5]

其中：E＝（Ex，Ey，Ez）为电场分量，H=（Hx，Hy，Hz）为磁场分量，对应的数值通量分别为[6]

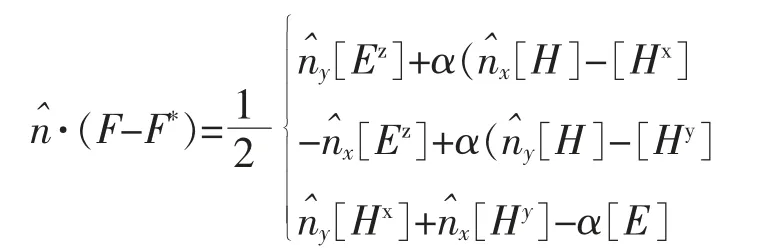
其中：（Hhx，Hhy，Ehz）为近似解。

1 局部格式

考虑Maxwell 调和形式方程

局部散度为零的条件为

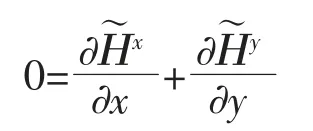
边界条件为

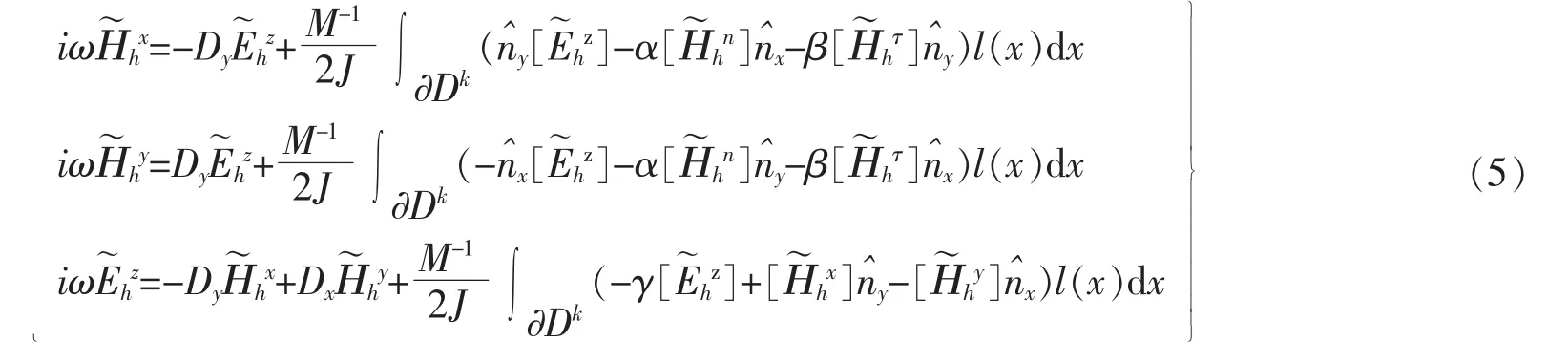
假设存在一个离散特征对ω=0，但（Hx，Hy，Hz）非零，则局部单元Lax-Fridrichs 格式为

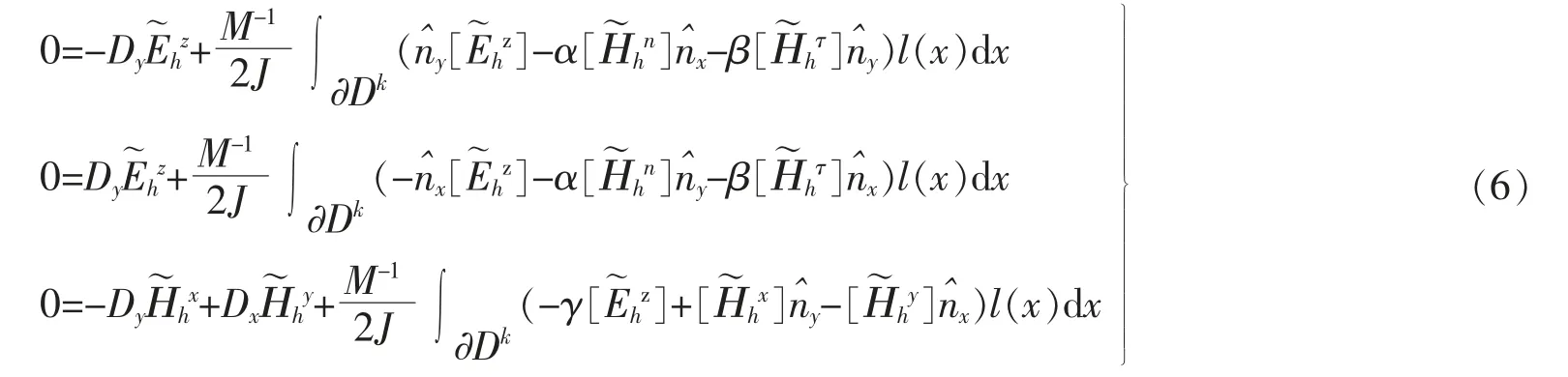
对于方程（5）格式，可以推出求解方程（4）的迎风格式［7-8］、非协调惩罚格式［9-10］、以及经 典 的Lax-Fridrichs 通量公式，由于谱方法中，测试函数通常是全局光滑的，取基函数与试验函数相同，得到

其中：α，β，γ 取任何非负数时，半离散格式L2稳定；当α=0，β=1，γ=1 时，该格式是迎风通量；当α=1，β=0，γ=1 时，该格式是惩罚通量；当α=1，β=1，γ=1 时，该格式是Lax-Fridrichs 通量。

2 数值算例

本节我们来讨论Maxwell 特征值问题谱方法的实用性与有效性，考虑二维Maxwell 方程

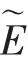
图1 用于计算理想边界条件金属方块域上特征值问题的交错网格Fig.1 Staggered grid for calculating eigenvalue problems over metal square domains with ideal boundary conditions

下面将运用两种不同的局部基函数，分别由迎风、惩罚和Lax-Fridrichs 通量来进行求解，一种是应用完备的N 阶多项式基，另一种是不同通量结合局部散度为零的基函数。

这个函数满足▽·φn=0，将磁场表示为

表1 给出了MATLAB 数值模拟完备多项式基N＝3 与N＝5 的数值结果， 可以看出该格式对方程可以达O（h2N+1）到阶精度。 表2 是局部散度为零的基函数对特征值得到的收敛阶，看到对N=3 收敛阶O（h2N+1），而由线性算子的条件数影响N＝5 的结果很不平稳。 表3 给出了惩罚通量格式完备多项式基N＝3 与N＝5 的数值结果，可以看出该格式对方程可以达到O（h2N-1）阶精度。 表4 是局部散度为零的基函数对特征值得到的收敛阶， 看到对N＝3 收敛阶O （h2N-1）， 而由线性算子的条件数影响N＝5 的结果很不平稳。 表5 给出了Lax-Fridrichs 格式完备多项式基N＝3 与N＝5 的数值结果，可以看出该格式对方程可以达到O（h2N+1）阶精度。 表6是局部散度为零的基函数对特征值得到的收敛阶，看到对N＝3 收敛阶O（h2N+1），而由线性算子的条件数影响N＝5 的结果很不平稳。

表1 具有迎风通量的前10 个特征值的收敛性Tab.1 Convergence for the first 10 eigenvalues of operator with an upwind flux

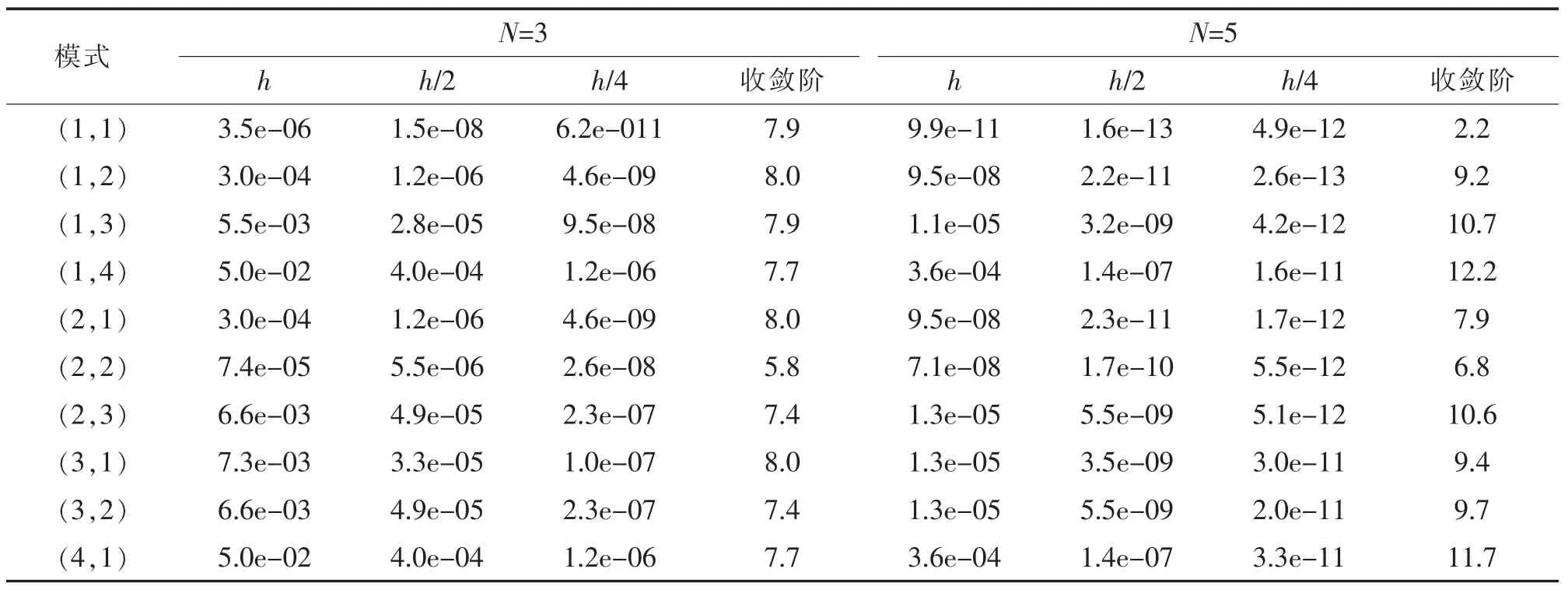
表2 局部散度为零的基对应迎风通量格式前10 个特征值的收敛性Tab.2 Convergence for the first 10 eigenvalues of operator with upwind flux and locally divergence-free basis

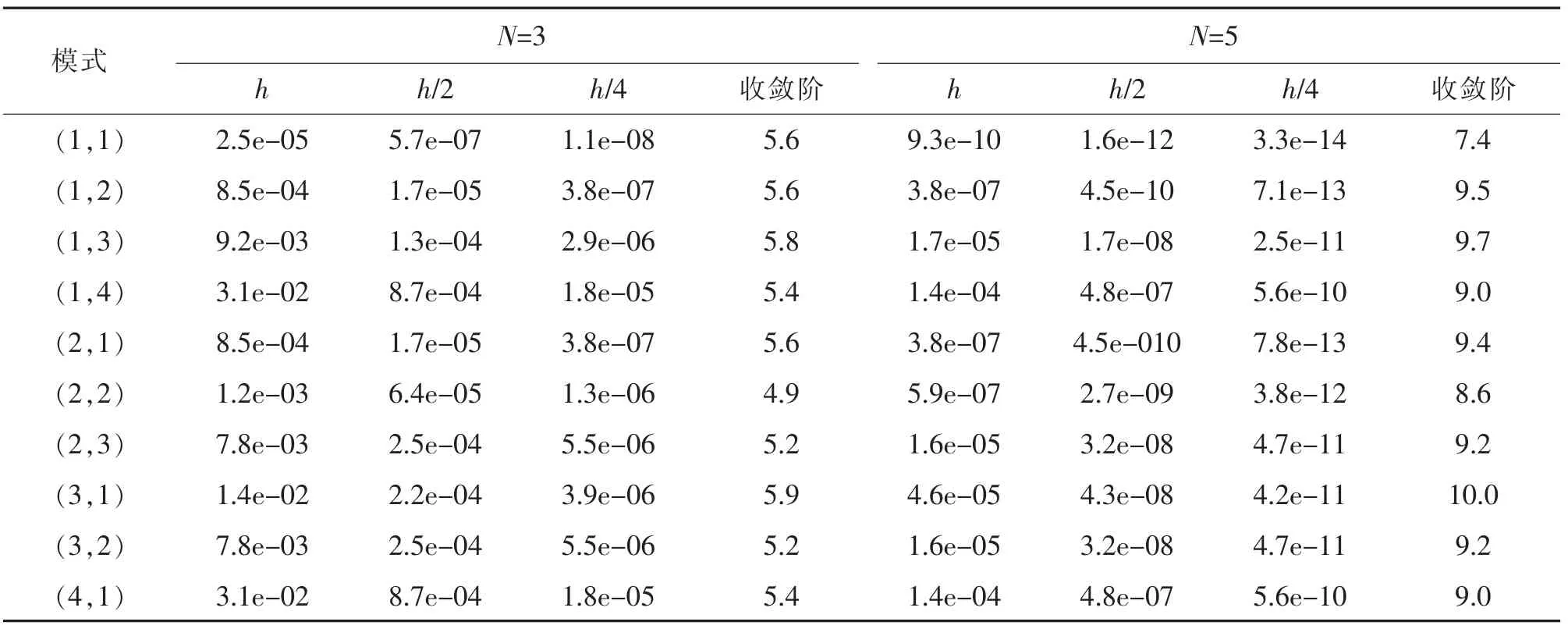
表3 具惩罚通量的前10 个特征值的收敛性Tab.3 Convergence for the first 10 eigenvalues of operator with a penalty flux

表4 局部散度为零的基对应惩罚通量格式前10 个特征值的收敛性Tab.4 Convergence for the first 10 eigenvalues of operator with penalty flux and locally divergence-free basis

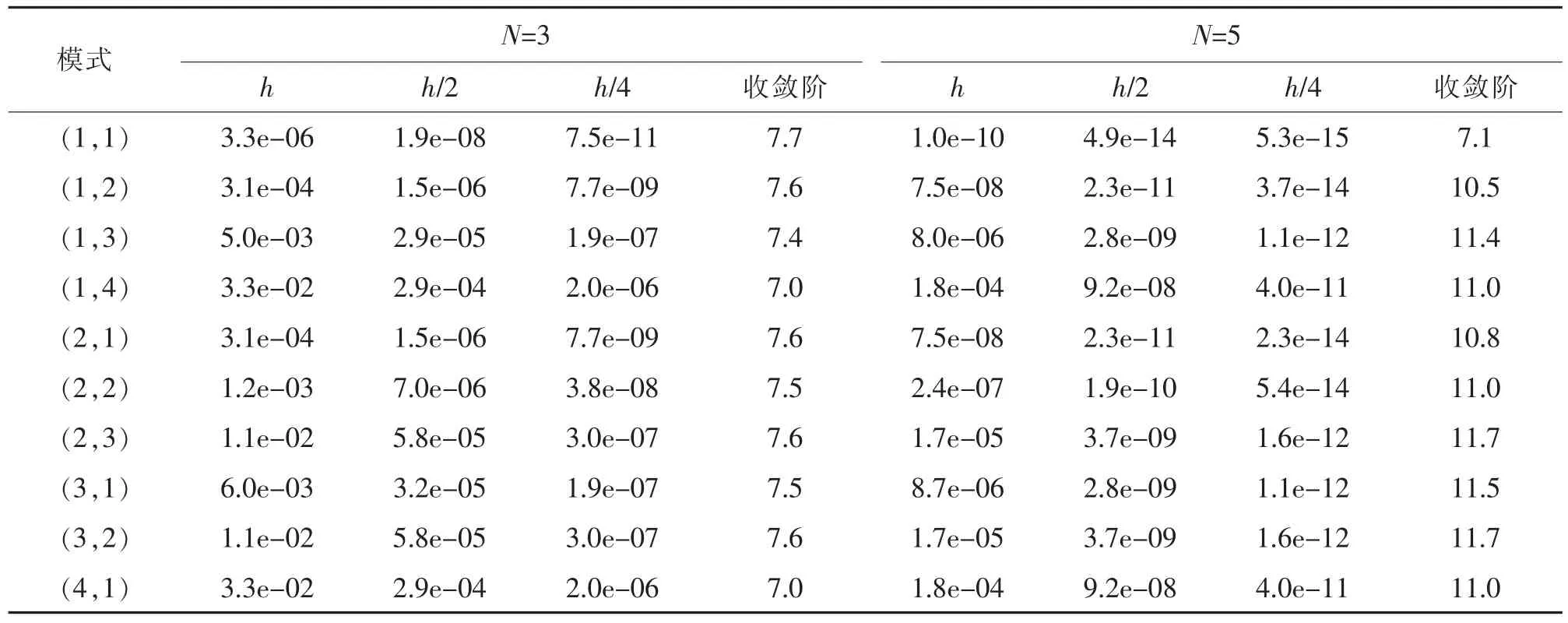
表5 具有Lax-Friedrichs 通量的前10 个特征值的收敛性Tab.5 Convergence for the first 10 eigenvalues of operator with Lax-Friedrichs flux

表6 局部散度为零的基对应Lax-Friedrichs 通量格式前10 个特征值的收敛性Tab.6 Convergence for the first 10 eigenvalues of operator with Lax-Friedrichs flux and locally divergence-free basis

从表1～表6 的结果可以看出，本文所运用的谱方法算法稳定可靠，所需迭代次数和计算时间虽然较大，特别迎风通量和惩罚格式互补，迎风通量用于惩罚磁场的切向分量，惩罚格式用于惩罚磁场的法向分量，但还是达到了相当好的收敛阶效果。