一类奇摄动Kdv-Burgers方程与孤波解
2020-09-18李瑞翔包立平吴立群
李瑞翔,包立平,吴立群
(杭州电子科技大学数学研究所,浙江 杭州 310018)
0 引 言
Kdv-Burgers方程常用于描述弛豫介质中有限振幅波的传播。Kdv-Burgers方程可以用来表述孤波,引起人们高度关注。孤波的形成是由于同时含有频散和非线性效应,两种效应最终达到互补从而形成一个形状不变的稳定局部扰动向前传播。文献[1]使用tanh方法给出Burgers方程、Kdv-Burgers方程的复解。文献[2]使用逆散射法求解摄动Kdv方程,给出精确的N-孤子解,并进一步研究2-孤子解情况下孤子的运动。文献[3-4]研究广义Burgers-Kdv方程行波的存在性和渐近性,给出相关常微分方程的异宿轨道,并用几何方法证明Burgers-Kdv方程行波解的存在性。文献[5]通过求解具有边界条件、行波速度、非线性强度和色散系数的椭圆方程,在零边界条件下,发现了孤立波。文献[6]使用Lyapunov-Schmidt方法,证明一类奇摄动非线性Schrödinger方程孤波解的存在,这些解集中在其势函数的非退化临界点处。但是,以上研究未涉及方程中的频散项,主要是通过逆散射、几何奇摄动等方法求解几类带高阶项的奇摄动问题。本文研究一类吸收项和弛豫项均带小参数的Kdv-Burgers方程,目的在于讨论吸收项和弛豫项对Kdv-Burgers方程产生扰动(孤子)的影响。
1 形式展开
根据文献[7],在弛豫介质中,有限振幅波的传播方程可以表示为带小参数ε的Kdv-Burgers方程:
(1)
式中,a,b是正常数,ε是非零小参数。假设φ(x)是与ε无关的函数且至少三阶连续可微。
求方程(1)的退化解
并代入方程(1),可得:
(2)
定理1方程(2)的解为u0=φ(x+u0t)。
证明方程(2)的特征方程为
求得隐函数解
u0=Ψ(x+u0t)
(3)
式中,函数Ψ是任意函数。式(3)代入方程(1)中的初值条件可知
u0(x,0)=Ψ(x)=φ(x)
因此式(3)可以写为:
u0=φ(x+u0t)
证毕。
根据定理1,求得方程(1)的外解。
接着求方程(1)的内解。对方程(1)做合成展开式,其零次幂项为:

(4)
式中,ξ=(x-ct)/ε,常数c是行波速。将式(4)代入方程(1)得:
(5)
定理2方程(5)存在孤子解。
证明在ξ是有限的情况下,x趋于0,此时
u0(x,t)=u0(ξε+ct,t)
(6)
式(6)按ε展开后取零次幂近似,有
u0(x,t)≈u0(ct,t)
(7)
式(7)右端是只与t有关的函数。方程(5)两边对ξ积分得:
(8)
(9)
再对式(9)两端积分并整理得:
因此
最终可得:
证毕。
根据定理2,求得方程(1)的内解。
2 余项估计
定理3方程(1)的渐近解的余项R满足
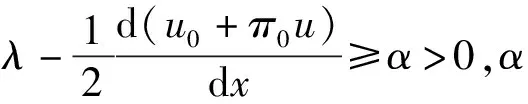
证明考虑方程(1)的余项

代入方程(1)得
化简得
(10)

令R=eλtP,λ为任意常数,代入式(10)得
(11)
令
其中,D=suppφ=[-N,N]×[0,T],D1=[-N-δ,-N]∪[N,N+δ]×[-δ,0]∪[T,T+δ],N是足够大的正常数,δ是足够小的正常数。
定义算子Lε,对满足式(11)的函数P,有
(12)
式中,(x,t)∈D。
事实上,对满足式(11)的任意函数ω,有
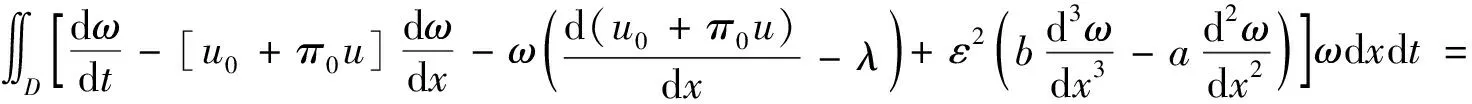
由式(12)得
因此
可得
(13)
式(13)右端与N无关,所以当N→∞时,等式依然成立。最终可得U(x,t,ε)在无界区域的渐近解一致有效。证毕。
3 结束语
本文讨论一类奇摄动Kdv-Burgers方程在无界区域上带初值条件的波运动问题,计算其形式渐近解,得到简单波与孤子解,并证明解的一致有效性,这表明该方程仍能在外解的某间断处产生孤子解。后期将对内外解展开式的高阶项做进一步研究,确定孤子解出现的位置,并研究高维奇摄动Kdv-Burgers方程问题。
