基于实时电流采样数据的超导电缆失超检测方法研究
2020-09-18张会明邓祥力张乾波张宏杰朱承治
张会明 丘 明 邓祥力 杨 梅 张乾波 张宏杰 朱承治
(1.中国电力科学研究院有限公司, 北京 100192;2.上海电力大学 电气工程学院, 上海 200090;3.国网浙江省电力有限公司, 杭州 310000)
对超导电缆失超的检测,国内外的研究主要集中在非电气量检测方法和电气量检测方法两方面.非电气量检测方法主要有检测超导输电线路的温度[1-2]、液氮对低温容器的压力[2]、液氮流速[3]等,根据失超过程中非电气量的变化特性,提出物理性的失超检测方法.但非电气量不能及时检测出来,且受外界环境影响大[4].电气量检测主要根据超导电缆的电流和电压电气量,提出能够反映失超状态的电气量特征,如幅值、相角等[5-8],具有速度快、检测精度高等优势.
由于投运的超导输电工程较少,获取数据样本少,试验系统成本高、系统复杂,因此数字仿真系统的建立对失超算法的仿真具有重要的意义.利用已有的研究成果,建立反映超导输电线路多状态的超导电缆数字仿真模型,有助于对算法的分析研究.超导电缆有稳态模型和暂态模型,稳态模型主要用于超导带材结构的最优化设计[9],暂态模型主要用于研究失超过程中电流的分布及温度变化.文献[10-13]研究了超导电缆在失超过程中,铜骨架和支撑层材料对分流的影响;文献[14-17]研究了超导电缆在短路冲击下电缆的温度分布;文献[18]精确考虑了超导带材间隙中的液氮冷却液在失超过程中对散热的影响;文献[19-21]建立了超导电缆失超过程中,电气和温度的耦合模型,用于仿真失超过程;文献[21-22]还利用电磁暂态仿真软件对模型进行了实现.
本文从简化的超导输电线路的稳态模型出发,求取了超导电缆在超导态的超导层和屏蔽层电流波形补偿系数;在暂态模型中,利用Hausdorff距离值对波形差异性进行度量,提出基于Hausdorff距离的失超检测方法.本文建立考虑铜骨架互感参数的超导电缆失超数字仿真模型,对波形差异失超检测方法进行了仿真,验证了所提方法的正确性.
1 超导电缆失超过程中电流波形差异性分析
含有多层超导传输层和屏蔽层的超导电缆的简化分析电路如图1所示.

图1 超导电缆失超电流分布
图中i1、i2和i3分别为流过铜骨架、超导层和屏蔽层的电流,Δu为超导电缆上产生的压降.Rf和Rc分别为铜骨架电阻和超导层电阻,Lf、Lc和Lm分别为铜骨架、超导层和屏蔽层的自感,Mfc、Mfm和Mcm分别为铜骨架、超导层和屏蔽层之间的互感.
1.1 正常运行超导态
设施加在超导电缆上的电压为工频电压Δu=Umcos(wt+θu),超导层电阻为0,铜骨架支路没有电流,那么i1为0,Rc为0,超导层和屏蔽层电流的大小如公式(1)所示:

所以,屏蔽层电流通过乘以补偿系数k1以后,和超导层电流完全相等,瞬时值波形完全重合,即Δi=i2-k1i3=0.
1.2 超导电缆暂态失超阶段
暂态失超过程中,超导电缆电阻逐渐增加,铜骨架和超导层支路中都会流过电流.在失超过程中,流过超导层的电流越小,在电感上的压降越小,即电感上的压降Δu1=Um1cos(wt+θu1),越小.其中,Um1受铜骨架电流,失超电阻等影响,在失超过程中越来越小,θu1与失超电阻的大小有关.超导层和屏蔽层的电流大小如式(2)所示.
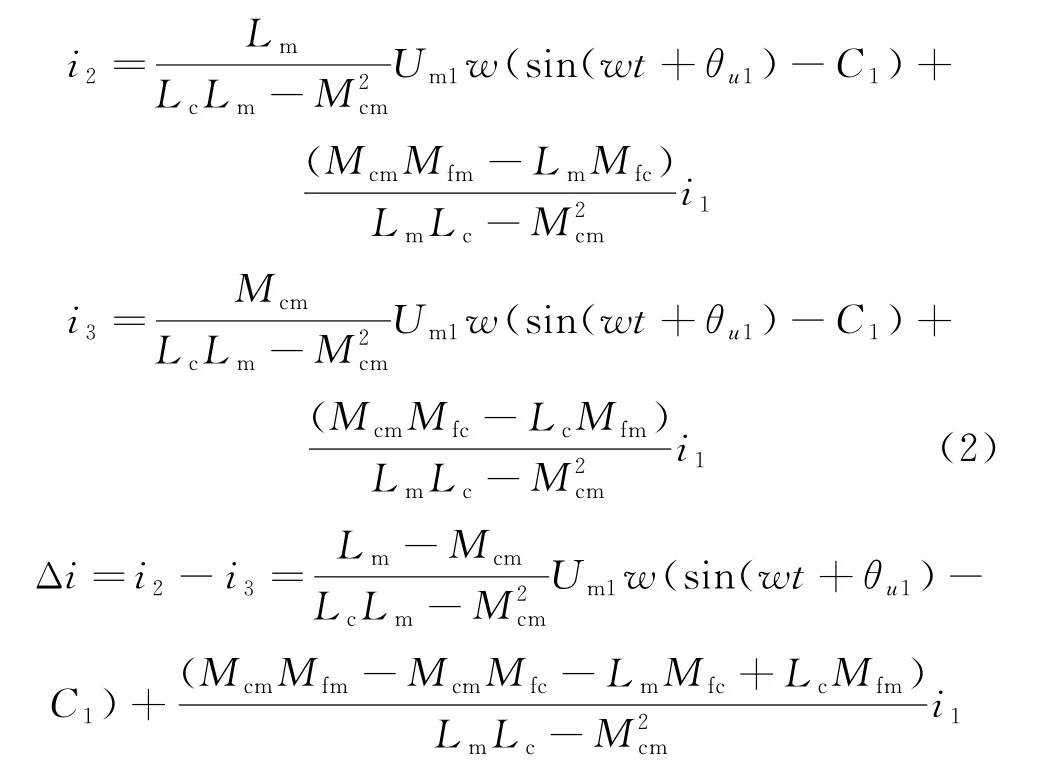
由上式可知,失超过程中的电流分布除了与自身的结构有关外,还与失超过程中的电阻,铜骨架的电流有关.由于McmMfm-McmMfc-LmMfc+LcMfm的值很小,约等于0,导体层与屏蔽层的电流差主要受电感压降的影响,即电流差异在失超过程中越来越小.
1.3 TA饱和对失超检测的影响
电网中发生故障时,超导电缆中流过的电流为:

其中:Tp为电网中的衰减时间常数;Ipm为短路前电流的幅值.
通过TA传变后,二次电流为:

式中:k2为TA的变比;i0为TA的励磁电流,电网正常运行时,其值接近为0.但电网中发生故障,出现很大的衰减直流分量时,电流公式如下:

其中:Ts为TA二次回路衰减时间常数;Tp为与电网频率和衰减时间常数相关的系数.
当电网发生故障时,超导电缆中流过的电流如公式(3)所示,其中包括衰减时间常数为Tp的非周期分量,经过TA传变,如公式(4),在二次电流中除了按照Tp衰减的分量以外,还有按照Ts衰减的分量,造成传变误差.在每个工频周期中,电流波形过零点的一段时间TA能够正确传变,随着直流分量的衰减,二次电流乘以TA变比后和一次电流重合,TA退出饱和状态.
2 基于Hausdorff距离计算的电流波形差异检测方法
2.1 波形差异度的计算
Hausdorff距离的计算能够满足对两个波形差异性的刻画(下文简称H距离).
定义两个电流波形采样点的集合A、B;那么A集合中的ai可以对应B集合中的某个点bj,ai到bj的距离由公式(6)计算:

其中,‖·‖为欧氏距离.
定义集合A到集合B的H距离单向距离为h(A,B),其值由公式(6)决定:

对于集合A和集合B来说有两个单相H距离,分别是h(A,B)和h(B,A),所以集合A和B之间的Hausdorff距离定义为两个单相距离的最大值,如公式(8):
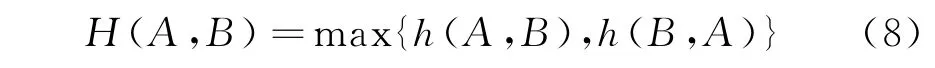
所以,可将两个电流波形差异性的评判转换为两个电流波形集合的H距离的大小,距离越大波形差异性越大.在H距离瞬时值计算数据窗时长tm内,利用超导层和屏蔽层的电流的n个采样点,分别形成集合A和B,计算集合A和集合B之间的H距离的瞬时值.其中,tm/n为采样间隔时间,计算起始时间为t1=(i-1)·tm/n,计算时长的结束时间为t2=tm+(i-1)·tm/n,i为数据采样点的序号,初始值为1;根据K1个连续H距离瞬时值计算H距离平均值Have,H距离算术平均值的计算公式为:

式中:Hj为超导电缆在第j个计算时长tm内的超导传输和屏蔽层电流波形之间的H距离.
考虑到检测误差和噪声干扰的影响,设置失超检测门槛值Hset,当上述距离平均值Have大于失超检测门槛值Hset时,确定超导电缆为失超状态.
2.2 TA饱和的判别
如前所述,电网中发生区外故障,TA剩磁很大并且一次电流中的衰减直流分量很大时,TA会产生直流饱和现象,使得失超检查判据误判别.如图2所示,在一个工频周期内,一次电流在过零点附近时,会进行一段时间的线性传变.通过对二次回路衰减时间常数的分析,在50 Hz频率的电网中,即在一个工频周期20 ms内,线性传变的时间不会少于3 ms.在一个工频周期内,如果数据窗长度为1 ms,至少有2 ms的时间内H距离是为0的,如图2所示.

图2 TA饱和时H距离值的计算示意图
3 超导电缆失超检验算法仿真
本文利用PSCAD/EMTDC和Matlab语言建立了如图3所示的超导电缆的失超检测仿真模型[23].

图3 失超检测仿真模型
利用PSCAD/EMTDC提供的接口程序,用Matlab计算电流与温度耦合过程的电阻值来修改PSCAD/EMTDC模型仿真过程中超导电缆电阻值.和超导电缆连接的两个电网等效为两个无穷大系统G1和G2,额定电压110 k V,T1和T2为Δ/Y0-11,容量250 MV·A,电压110/35 k V的变压器,绕组电阻和漏电感分别为(标幺值):0.002和0.08.HTS为三相超导电缆传输层,SL为三相超导电缆屏蔽层,TA1、TA2、TA3和TA4为电流互感器,用于采集传输层和屏蔽层电流.仿真步长为0.01 ms,仿真时间为0.1 s.
利用以上仿真模型对本文提出的H距离识别方法和电流有效值以及相角识别方法进行了仿真.3种方法的参数整定如下:波形识别失超检测方法Hset整定为0.5,闭锁条件为每个周波(20 ms)H距离连续大于0.5的时间小于18 ms;电流比值法的有效值幅值比整定为1.2;相角差法的相位差整定为1 700.
3.1 TA正确传变的超导电缆失超态仿真
仿真中超导电缆的温度设定为77 K,超导电缆流过不同电流时,3种判据的检测结果如图4~5所示.

图4 温度为77 K时,电缆中电流变化时的超导层和屏蔽层电流的有效值比、相位差、H距离
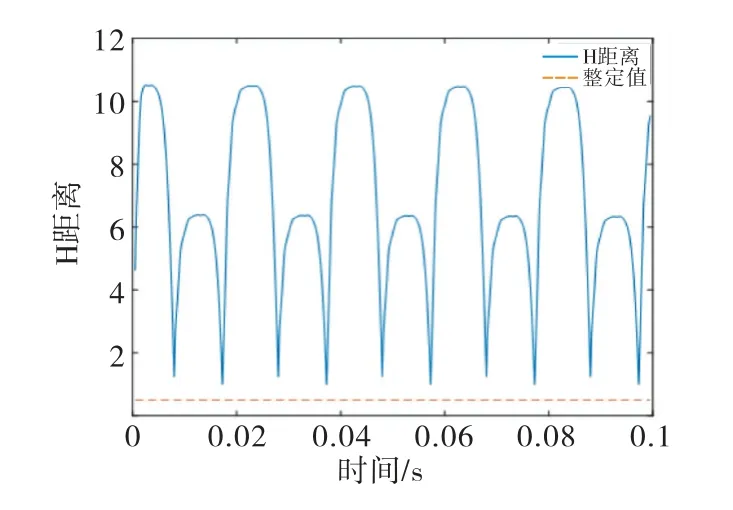
图5 电流为10 k A,温度为77 K时的H距离
从图4,图5中可以看出,当超导电缆失超时,电流比值法,相位差法,H距离均可检测到超导电缆的失超.失超发生时,流过超导层的电流达到失超临界电流,流过超导层电感的电压降达到最大值,电流大小差别最明显.流过超导电缆的电流越大,失超电阻越大,超导电缆中的电压电流的相角越偏离180°,即超导层与屏蔽层的电流相角越来越偏离180°,波形差异也越来越大,即H距离也越来越大.
图6表示超导电缆电流设定为20 k A,失超过程中温度变化时3种判据的检测结果.

图6 电流为20 k A,温度变化时的电流比、相位差、H距离均值
由结果可知,当失超严重时,电流比值法不能检测出失超.在失超过程中,由于热量的积累,温度升高,临界电流越来越小,失超电阻越来越大,超导层与屏蔽层的相角差越来越偏移180°,流过超导层的电流减小,超导层上的电感压降减少,因此屏蔽层的电流以及屏蔽层与超导层的电流差值也减少,波形差异也相对减少.
3.2 TA饱和对失超检测的影响
为了研究TA饱和对失超检测的影响,定义TA的饱和度SD,如公式(10)所示:
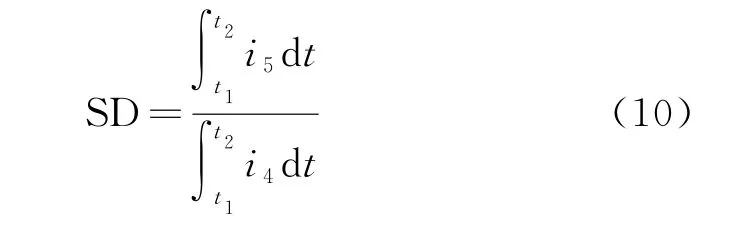
其中:i4为折算后TA一次侧电流;i5为TA二次侧电流.TA的饱和程度越高,SD的数值越大.
假设超导层电流通过TA以后发生畸变,屏蔽层电流正确传导.TA饱和对应的H距离如图7所示.在每个工频周期,饱和时每个工频周期内小于Hset的时间大于2 ms.随着TA饱和程度的加深,屏蔽层波形缺失的面积越来越大,3种判据的结果如图8所示.
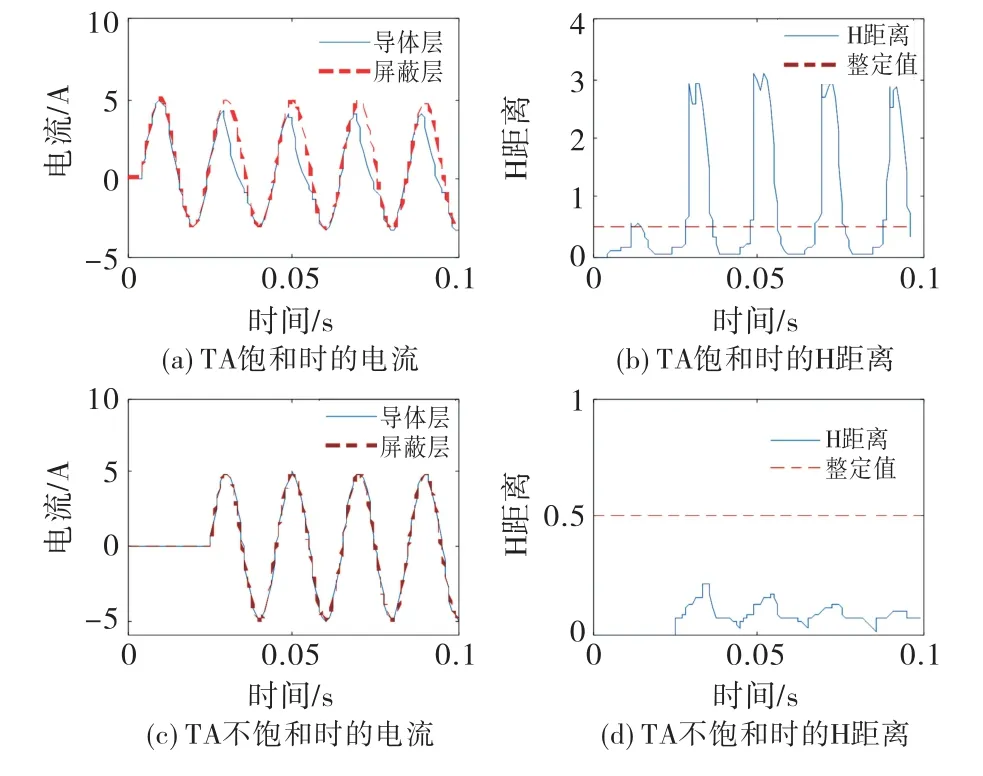
图7 互感器饱和与不饱和的H距离差异
当SD超过24.76%时,电流有效值比不能区分互感器饱和与超导失超;当SD超过40%时,相角差法不能区分互感器饱和与超导失超;当SD超过7.5%时,波形检测法满足闭锁条件,判断为不失超.
从图4和图6可以看出,H距离均值法对超导层和屏蔽层电流的波形差异性进行识别,在轻微失超和严重失超时比传统的基于幅值和相角的方法具有更高的灵敏度.从图8可以看出,幅值检测法在互感器饱和严重和失超严重时均不能正确检测,相位差法在互感器饱和时易误判断;H距离检测法因互感器饱和时H距离波形有明显的间断角,失超状态时H距离波形没有间断角,可以用来用来区分互感器饱和与超导电缆失超,比幅值法和相角法具有更高的灵敏度.
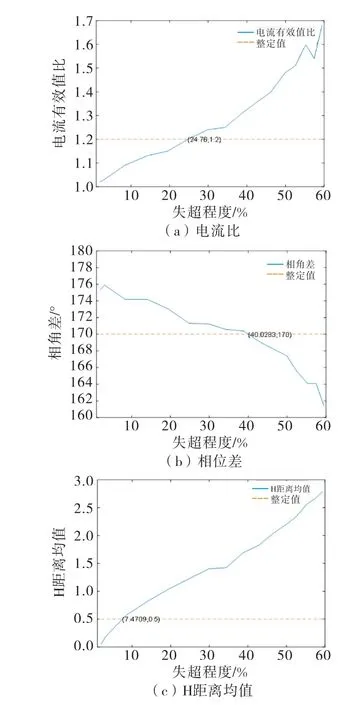
图8 超导态时,不同程度互感器饱和的电流有效值比值,相位差,H距离均值
4 结 语
本文通过分析超导电缆在超导态和失超过程中,超导层和屏蔽层电流波形差异性的电气量特征,提出了基于H距离的电流波形差异的超导电缆失超检测方法,有以下几点结论:
1)通过简化的超导电缆数学模型的分析,在超导态时,屏蔽层电流补偿后和超导层电流完全重合,没有差异性.在失超暂态过程中,电流波形出现差异性.可用波形的差异性来做失超检测.
2)考虑超导层和屏蔽层电流差波形,在超导电缆失超和TA饱和的情况下的差异,提出了超导态情况下TA饱和的闭锁判据,用于TA饱和对失超检测判据的闭锁.
3)基于H距离反映电流差异度的失超检测方法能够快速灵敏地检测出超导电缆的失超状态,通过对本文提出的算法和传统失超检测判别方法的比较仿真,验证了本文算法的优越性.
