铅铋合金中颗粒物对弯管的冲蚀研究
2020-09-18杜晓超袁显宝张彬航
杜晓超 刘 鹏 洪 锋 袁显宝 张彬航
(三峡大学 机械与动力学院, 湖北 宜昌 443002)
铅铋合金由于具有良好的中子学和热工水力学特性,已成为第四代先进核反应堆、加速器驱动次临界核能系统以及聚变堆冷却剂或散裂靶的主要候选材料之一[1-2].但是铅铋合金对直接暴露在其中的钢材具有较强腐蚀性.实验研究表明,不锈钢样品表面因腐蚀脱落产生的固相杂质从微米到几百微米不等[2],因此高温铅铋合金对管路造成腐蚀和冲刷将产生大量的腐蚀产物等固态颗粒物.从而流动的铅铋合金系统中不可避免地会存在一些杂质,其中熔点较高的杂质因为不能熔化而在铅铋流体中以颗粒物形式存在[3],在管道系统中最终形成铅铋合金夹带着固体颗粒一起流动的运动状态.夹杂颗粒物的铅铋合金流体对管道的冲刷与腐蚀不是简单的叠加.首先,冲刷能加速传质过程,促进氧到达管壁的表面,同时由于冲刷作用,腐蚀产物脱离材料表面,从而加速腐蚀;冲刷的力学作用使管壁的氧化膜减薄、破裂或使材料发生塑性变形、应力聚集,从而加速局部腐蚀.冲刷也会造成氧化膜表面出现凹凸不平的冲蚀坑[4-5],造成微湍流的形成,导致冲蚀增强[6].另外,起保护作用的氧化膜表层结构较为疏松[7-8],在强冲蚀作用下很容易造成氧化膜脱落或减薄,这对于保护性氧化膜的影响是不容忽视的.
目前,对于管道壁面材料冲蚀的研究主要有水中颗粒物、油中颗粒物和气体中颗粒物对管道的冲蚀[9-10],研究成果较多;但是对铅铋合金中颗粒物的研究较少,主要有周涛,杨瑞昌,胡雨,等[11]对亚微米颗粒在Sierpinski海绵模型中热泳沉积做了研究;刘亮,周涛,杨旭,等[12]对铅铋合金中颗粒物的沉积做了研究,并且设计了一种防铅铋合金中颗粒物沉积的管道;杨旭,周涛,方晓璐,等[13]对矩形通道内不溶性腐蚀产物的沉积分布进行了研究;陈娟,周涛,方晓璐,等[14]对纳米颗粒在液态金属内的热泳规律进行了研究;雷玉成,陈钢,朱强,等[3-4]的研究表明,铅铋合金中剥落的氧化物对管壁氧化膜的冲蚀作用不能忽略;颗粒物对管道壁面冲蚀磨损问题的更进一步详细的研究未见文献报道,另外,铅铋合金开展实验研究相对困难[15],采用数值模拟方法对相关问题开展理论分析,对液态铅铋合金中颗粒物对管道壁面的冲蚀研究很有意义.
1 计算模型
1.1 离散相控制方程
在DPM离散相模型中,流场中颗粒的运动轨迹是通过对拉氏坐标系下的颗粒作用力微分方程进行积分得到的,颗粒的作用力平衡方程为:

式中:up为离散相颗粒速度(m/s);u为连续相液相速度(m/s);FD(u-up)为单位质量颗粒受到的阻力(N);Fx为其他方向上的作用力(N);gx为x方向重力加速度(m/s2);ρ为连续相密度(kg/m3);ρp为离散相颗粒密度(kg/m3).其中:
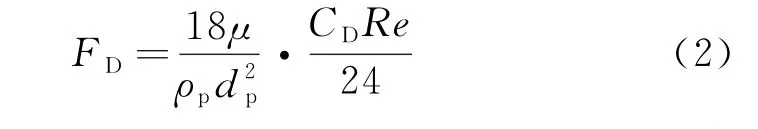
式中:μ为连续相黏度(Pa·s);dp为离散相颗粒直径(m);CD为曳力系数;Re为相对雷诺数.

式中:对于球形颗粒,a1,a2,a3在一定雷诺数范围内是常数.
1.2 冲蚀磨损模型
在Fluent中定义的冲蚀模型采用冲蚀磨损率表示.冲蚀磨损率是指固体颗粒物以一定的速度冲刷靶材所造成的磨损速率,即高速运动的颗粒物在单位时间内对单位面积的靶材所造成的磨损质量.冲蚀速率表达式为:

式中:Rerosion为壁面磨损速率[kg/(m2·s)];N为碰撞颗粒数目;mp为颗粒质量流量(kg/s);C(dp)为颗粒直径函数;θ为颗粒对壁面的碰撞角(°);f(θ)为侵入角函数(m/s);up为颗粒相对于壁面的速率(m/s);b(v)为相对速率函数;Aface为壁面计算单元的面积(m2).
其中C(dp)取为1.8×10-9,b(v)取为2.6.侵入角函数f(θ)对于冲蚀现象是一个重要的参数,参考Finnie、Levy、Foley等[16-18]的工作,在不失参考价值前提下采用保守数据进行计算;在Fluent中采用分段线性方式进行定义,数据见表1.

表1 侵入角函数表
固体颗粒与壁面发生碰撞时存在能量转移和能量损失,主要表现在碰撞前后速度分量的变化.通常以碰撞前后速度分量的比值衡量能量的损失情况,并将该比值定义为恢复系数,本文参考文献[19-22]总结获得的恢复系数公式为:

式中:eN为法向恢复系数;eT为切向恢复系数.
2 模拟计算基础
采用Fluent程序对夹杂固态颗粒的铅铋合金的流动规律进行模拟.
2.1 物性数据库
由于Fluent自带的数据库没有铅铋合金,所以需要在Fluent中创建新材料的物性数据库.本次计算中关联紧密的是流体力学和热物性参数[23,24],其中主要经验关系式见表2.
代数方程的求解全部采用SIMPLE算法,方程的求解差分方式采用标准差分方式,湍流动能k、以及动量和能量等均采用二阶迎风差分格式,这种格式使得计算的速度较快,同时又具有较好的精度和收敛性;选择双向耦合方式,即颗粒物能影响流场,同时流场的参数变化又会反过来对颗粒物的运动产生影响.分别计算不同颗粒密度下的冲蚀,以及不同流速、不同颗粒质量流量、不同温度、不同粒径下的冲蚀情况.

表2 液态LBE物性参数经验关系式
2.2 建立模型
使用Solidworks软件创建管径为D(D=38.1 mm),弯管角度为α的管道模型,如图1(a)所示.为研究弯管形状的影响,建立了从α=0°到α=90°的10个不同角度的弯管模型分别进行计算.将模型导入Icem中进行网格划分,为了反映近壁面处各物理参数的剧烈变化,对管道壁面处的网格进行加密,设置了5层边界层,如图1(b)所示,经过网格无关化验证,网格数为15万左右.

图1 管道模型和截面网格
模拟仿真中的连续相为液态铅铋合金,入口处的边界条件为速度入口(velocity inlet),出口处的边界条件为自由出口(outflow),管壁的边界条件设置为“wall”类型,属性设置为“reflect”,表示颗粒碰撞壁面后反弹,侵入角函数以及恢复系数在此属性里进行设置.
3 模拟计算结果与分析
3.1 颗粒粒径对冲蚀位置的影响
参考A.Marino[25-27]等在CRAFT回路上的实验研究以及CFD仿真,模拟计算了温度为623.15 K、流速为0.2 m/s(管径为38.1 mm时质量流量为2.4 kg/s)的铅铋合金流体的流动规律,主要分析夹杂固体颗粒的铅铋合金对管壁的冲蚀作用.此次计算中,模拟了颗粒物直径从1~1000μm时两相流对管壁的冲蚀速率,分别选取了10个1~10μm的颗粒粒径、10个10~100μm的颗粒粒径、10个100~1 000μm的颗粒粒径,共完成300个算例.
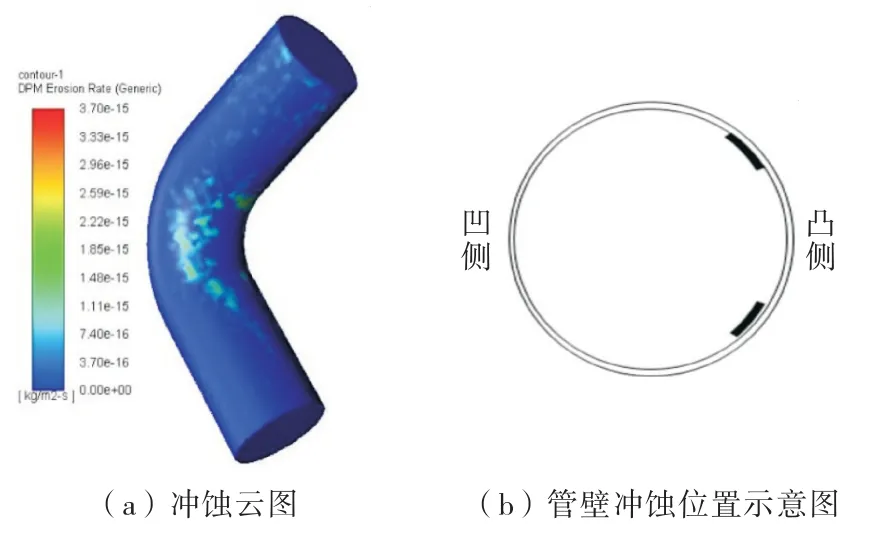
计算发现,夹杂不同粒径颗粒物的两相流,其对管壁的冲蚀作用位置也不同.颗粒粒径d<10μm时,冲蚀位置相对集中,冲蚀发生在弯管凸侧,冲蚀云图如图2(a)所示;随着颗粒粒径增加,冲蚀位置开始变得分散,围绕弯管凸侧附近,沿周向有向两边扩散的分布趋势,图3所示为颗粒粒径10μm 图2 粒径为1~10μm的颗粒冲蚀情况图 图3 粒径为10~100μm的颗粒冲蚀情况图 图4 粒径为100~1 000μm的颗粒冲蚀情况图 出现这一现象的原因主要是: 1)小粒径颗粒(1μm 2)大粒径颗粒(d>100μm)的冲蚀位置在管道凹侧:随着粒径的增加,颗粒物在流场中的跟随性逐步减弱,当颗粒粒径10μm 由于铅铋合金中腐蚀产物和析出物情况复杂,可能存在各种尺寸固态颗粒,计算夹杂不同粒径颗粒的铅铋合金流体对管道壁面的冲蚀作用就很有必要.在所建弯管模型上分别计算,结果如图5所示. 图5 不同粒径下的冲蚀速率 可以看出,当固态颗粒的粒径d<100μm时,两相流体对管壁的冲蚀速率较小,且随弯管角度的增加而增加的幅度很小,特别是粒径在10μm 铅铋合金工作系统往往是非等温回路系统,由高温段和低温段一起构成闭合循环回路.例如,CRAFT回路[25-27]的铅铋合金温度在573.15 K至773.15 K之间,因此在流动的铅铋合金系统中需要考虑温度的影响.选取管径为38.1 mm、几个不同角度的弯管为研究对象,设定颗粒粒径为100μm,铅铋流体的流速为0.2 m/s(管径为38.1 mm时质量流量为2.4 kg/s),分析不同温度下流体的冲蚀速率.计算结果如图6所示. 图6 不同温度下的冲蚀速率 由图6可以看出,流体的冲蚀速率随温度的升高而减小,在直管中减小的程度较弱,从573.15 K时的1.226×10-14kg/(m2·s)降为773.15 K的1.001×10-14kg/(m2·s),降幅约为17%;在40°的管道中,从573.15 K时的5.248×10-14kg/(m2·s)降为773.15 K的3.616×10-14kg/(m2·s),降幅约为31%.即,温度对流体冲蚀速率的影响为负效果,流体温度越高,流体对管壁冲蚀速率越小.造成此结果的主要原因,在于温度对颗粒冲蚀速率的影响是源于铅铋合金物性参数的变化,铅铋合金的密度以及黏度随温度的升高而降低,导致铅铋合金对颗粒的曳力、压差力等降低,进而颗粒的跟随性变差,从而对管道的冲蚀速率降低. 考虑弯管角度的影响,分别建立了弯管角度从0°增加到90°时10个不同的管道模型,分析流体对管道的冲蚀速率.设定颗粒粒径为100μm、管径为38.1 mm、流速为0.2 m/s(管径为38.1 mm时质量流量为2.4 kg/s),不同温度的金属流体温度对管壁的冲蚀速率,计算结果如图7所示.图中的点是模型计算结果,实线为数据拟合结果,通过对不同温度的计算结果进行线性拟合处理发现,流体的冲蚀速率随着弯管角度的增加而增加. 在573.15 K时,直管中流体对壁面冲蚀速率为1.226×10-14kg/(m2·s),90°的弯管中的冲蚀速率为7.454×10-14kg/(m2·s),约为直管中流体冲蚀速率的6倍;在773.15 K时,直管的冲蚀速率为1.001×10-14kg/(m2·s),90°弯管的冲蚀速率为3.172×10-14kg/(m2·s),约为直管冲蚀速率的3倍.即,在低温时弯管角度对流体冲蚀速率的影响明显. 图7 不同弯管角度的冲蚀速率 铅铋合金是典型的重金属材料,其密度大约是水的10倍,且铅铋合金与传统的结构材料相容性较差,工程应用中会不可避免地生成固态产物,夹杂颗粒物的铅铋合金的冲蚀现象是不能忽视的重要问题.本文基于CFD方法对影响铅铋合金中颗粒物对管壁冲蚀的相关参数进行了计算分析,利用Fluent对管壁的冲蚀问题进行了数值模拟. 1)不同粒径的颗粒物对弯管管壁的冲蚀位置不同,夹杂小颗粒的流体冲蚀作用在弯管内壁的凸侧,大颗粒流体的冲蚀作用在弯管内壁的凹侧. 2)不同粒径的颗粒物对弯管壁面的冲蚀速率不同,随着夹杂的颗粒物粒径增加,铅铋合金的冲蚀速率先减小后持豫,随后迅速增加,当粒径d>100μm时,夹杂流体对管壁的冲蚀作用影响较大.故应设置净化装置,将冲蚀速率降至最低. 3)夹杂颗粒物的铅铋合金流体,低温时冲蚀速率较大,高温时冲蚀速率较小.不同弯管角度中的冲蚀情况也不同,且弯管角度对冲蚀速率的影响受温度影响,整体上看,冲蚀速率随着弯管角度的增加而增加.

3.2 颗粒粒径对冲蚀速率的影响

3.3 温度对冲蚀速率的影响

3.4 弯管角度对冲蚀速率的影响

4 结 论
