梯形滑块在直线与圆弧导轨过渡阶段行走曲线的分析与研究

蔡吉飞 位士博 郭凯明

直线导轨与曲线导轨过渡曲线对滑块运转性能起着十分重要的作用。通过对滑块在直曲线和圆弧导轨上各阶段工作要求分析，给出了滑块运动轨迹的求解方程，得出了确定圆弧导轨半径参数的基本方法。通过对导轨系统结构和速度分析，给出了影响圆弧导轨半径尺寸的相关因素，得到了其振动频率的求解方法。

导轨作为机械设备上一种零部件，现已形成了标准化、通用化生产，在机械设备上得到了广泛应用，如图1所示。目前所使用的导轨主要以直线导轨或环形导轨为主，曲线导轨使用很少，主要是造价远高于常规的直线或圆形导轨。很多企业都把曲线导轨设计的相关资料列为机密技术，不向外界透露任何信息。本文针对梯形滑块从直线导轨到曲线导轨过渡时的行走曲线进行了分析研究，为需要这类技术人员提供一点帮助和支持。

环形导轨设计的关键是直线和直线之间的过渡段。这个过渡段多数是用圆弧直接过渡的一段式结构，有的则是用过渡曲线+圆弧曲线+过渡曲线的三段式结构。直接采用圆弧过渡曲线，结构简单，加工成本低。但由直线段到圆弧段存在的问题是法向加速度出现跳跃式突变，容易产生冲击和振动。

梯形滑块在导轨上的运动过程分析

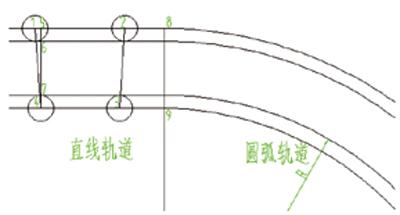
由滑块上的1、2、3、4点组成的梯形滑块（如果不需要转弯，则选用矩形滑块即可）如图2所示。当前的滑块位于直线导轨上，导轨的宽度为l67，滚子的半径为l47，则可由梯形边长参数求出导轨的宽度。

由于工作环境、导轨误差等多种因素，要保证滑块能够自由移动，l67至少要有负公差0.05～0.1mm。过大误差，滑块可能会摆动;过小误差，滑块可能会卡死。

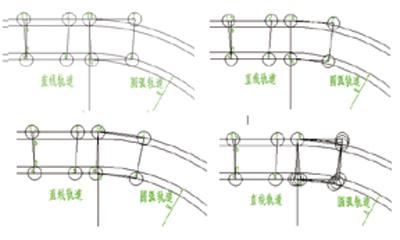
滑块上面的点2从圆弧轨道外侧起始点8的位置开始进入圆弧形轨道。假如滑块仍然处于直行状态，则滑块各项指标要求同前，如图3的左上角图所示。当梯形滑块上面的点1移动到圆弧轨道外侧起始点8时，如果滑块上的点2仍然保持水平状态，则后面的导轨仍然是直线导轨。如果滑块上的点3刚好到达圆弧轨道内侧起始点9的位置，如图3的右上角所示，这时梯形滑块底边已经向下倾斜了一个角度。如果滑块上的点3与垂直线有一个向左侧的倾斜角度，且这个角度与梯形滑块滑块上的点1、点5、点7这3点组成的小三角形内最小角相等，如图3的左下角所示。这时的圆弧半径R即为所允许的最小Rmin，如果再小于这个值，滑块就会与导轨之间硬性卡死。因此圆弧导轨R的取值区间为（Rmin，+∞），如图3的右下角所示。

R的值越来越大时，圆弧导轨就越来越接近直线导轨，其占用的空间也随之越来越大，从而导致机器的体积和圆弧导轨的加工成本都要大幅度增加。要找到一个比较理想的R值，既能够不增加成本，又能够使滑块前进的阻力最小，就需要对可能的R值进行研究分析。如图3右下角所示，这是梯形滑块可能的几个位置状态，其中一个状态是梯形滑块上的点1和点4在同一条垂直线上（如图3左下角图所示，滑块上的点1和点4与垂直直线上的圆弧轨道外侧起始点8和圆弧轨道内侧起始点9重合）。这时梯形滑块的斜边14与直线导轨处于垂直状态，因而其与直线轨道之间的间隙最大（假定圆弧轨道的径向宽度与直线导轨宽度相等）。如果后面联接的圆弧半径選择这个值，则滑块转弯的难度最低。这个圆弧的半径就是由滑块在4个点等腰梯形延伸成三角形的斜边长度：

滑块运动曲线各阶段过程分析

1.直线与圆弧之间的过渡曲线分析

从上面分析可以看出，如果由直线直接过渡到圆弧，则会出现梯形滑块运动轨迹曲率半径发生变化，由无线大直接变成图中的圆弧半径R值，这个跳跃就会产生振动，导致梯形滑块上的滚子与滑道产生冲击。因此理想的梯形滑块运动轨迹的曲线应该是曲率半径是渐变的，从而使梯形滑块在运动过程中不产生冲击或者产生的冲击尽可能小。假定梯形滑块上的点2从圆弧轨道外侧起始点8位置开始进入过渡曲线，当滑块上的点1到达圆弧轨道外侧起始点8位置时，这时滑块上的点1与点2同时与曲线导轨开始接触，这个过渡曲线的直线距离就是梯形的底边。

显然要使过渡曲线与两端平稳衔接，则必须采用样条曲线，即保持位移和一阶导数连续，则过渡曲线的表达式可以表示为：

（x，y）为圆弧中心坐标，而圆弧中心即为坐标系的原点。如果坐标系中心不在圆心，则可通过坐标系转换来求得转换结果。根据两端的边界条件，即可求出4个系数值，从而求得x，y之间的函数关系，画出过渡曲线。

上面用简单的样条曲线将直线导轨与圆弧导轨连接起来，但理论上还有很多问题要考虑，如这段曲线必须要求是外凸形的，即曲率中心必须在轨道内侧;同时还要求两端的连接过渡要平稳，交接时不出现抖动，则至少要求两端连接点3阶及4阶以上导数连续（需要采用7阶以上多项式连接，如下面公式所示）。两端的参数直线段上各阶导数都为0，圆弧上的各阶导数可用圆弧方程连续求导得出。

理论计算结果如图3所示。图3中的左上角为位移曲线，右上角为一阶导数曲线，左下角为二阶导数曲线，右下角为三阶导数曲线。从一阶异数曲线可以看出，位移曲线应该是连续光滑的（曲线上无折点）;从二阶导数曲线可以看出，位移曲线应该是内凹的（二阶导数全部为负值）;从三阶导数曲线可以看出，内凹的过程墨迹是渐近的（三阶导数是连续的）。这种过渡曲线理论上显然可以满足高速滑块运转的要求。

2.滑块从过渡曲线到圆弧之间的过渡过程分析

当滑块长边的前端点进入到圆弧轨道表面时，滑块长边的后端点正好到达过渡曲线上，这时可根据几何关系求出梯形滑块上面点3的运动轨迹，因为滑块上面点4此时已经进入圆弧轨道的内径上，运动轨迹已经确定。当然也可假定滑块上的点1的轨迹与滑块上的点2的轨迹完全相同，则根据滑块上的点2的两个约束条件（一是滑块上的点2与滑块上的点1之间距离为固定值，即梯形底边的长度;二是滑块上的点2在圆弧表面，满足其坐标的平方和为固定值）来求得梯形短边上滑块上的点3和滑块上的点4两个点的运动轨迹。实际上这种求解编程更为方便，本程序最后求解即采用这个计算公式。

3.滑块在圆弧曲线上的运动过程分析

当滑块长边的后端点进入到圆弧表面时，滑块上面与轨道接触的4个点全部到达圆弧曲线上，这时滑块和圆弧轨道处于理想接触状态。理论分析可以看出，只有梯形滑块的上底和下底边都在同心圆上，滑块才可以在圆弧轨道上无间隙移动。据此推理，圆弧轨道的径向宽度要大于直线导轨的宽度。

4.滑块从圆弧到垂直导轨的过渡曲线分析

当梯形滑块长边的前端点到达圆弧曲线的末端时，开始进入过渡曲线。这段过渡曲线可从前一段过渡曲线以45°角为对称轴镜像得到（即对称曲线），因此曲线上的各点坐标值可直接通过坐标变换来得到。

5.滑块从过渡曲线到垂直导轨的运动过程分析

由于滑块长边的前端点已经进入到垂直直线上，滑块长边的后端点进入到过渡曲线上。因此可通过梯形长边约束和过渡曲线上的点及梯形长边前端点坐标的x值，可求出梯形长边前端点坐标的y值。

滑块运动轨迹求解过程及运动误差的进一步分析

1.求解方法可进一步简化，编程更加方便

上述是对滑块在每一阶段的运动轨迹做了详细分析，并给出了求解方法。更简单的方法就是让滑块在起始的水平位置与过渡曲线或圆弧曲线之间留有一段水平运动轨迹（直线段），即滑块第一段运动轨迹为直线，第二段运动轨迹为过渡曲线，第三段运动轨迹为圆弧，则后面的运动轨迹都可通过镜像得到，不需要再做进一步讨论。假如是90°的圆弧导轨，则可以45°直线镜像得到后半部分曲线;如果是半圆弧导轨则可以通过圆心的水平直线镜像得到后半部分曲线。

2.滑块运动轨迹的误差分析

假定在采用过渡曲线的条件下，梯形长边的前端点和后端点都在轨道外侧的曲线上，则梯形短边后端点刚进入导轨时与短边前端点的起始位置之间存在误差。如果此值为零，则表示重合;如果不为零，则表明有运动误差存在，可能会影响滑块的运动精度。

假定在不采用过渡曲线的条件下，梯形长边的前端点和后端点都在轨道外侧的圆弧曲线上，则梯形短边后端点刚进入导轨时与短边前端点的起始位置之间的误差。如果此值为零，则表示重合;如果不为零，则表明有运动误差存在。如果要求导轨在直线上和圆弧上与导轨之间间隙都接近于零，则直线导轨和圆弧导轨过渡点必然有一个跳跃，从而可能会导致滑块前行时与圆弧导轨的跳跃部分形成冲击，所以必须将这个跳跃打成斜坡，保证滑块向前运动不受直接撞击。当然在滑块由圆弧导轨进入直线导轨时又会产生二次冲击。

根据滑块的运动规律，滑块进入圆弧轨道时要向外形成离心力，因而圆弧轨道内侧与直线导轨之间最好光滑过度，外侧与圆弧导轨之间可用斜坡过渡（如果不在一条直线上或者宽度不相等的话）。上面提到的过渡曲线也应首先保证内侧曲线为平滑过渡曲线。

3.圆弧导轨参数的影响因素分析

①圆弧导轨内外径设计分析

假如圆弧轨道的半径为前述的最小值，即滑块进入圆弧轨道后，梯形斜边14与23线重合，这是后接圆弧轨道半径所允许的最小值。如果再继续增加摆动角度的话，梯形滑块就会与导轨之间卡死。同时在梯形滑块摆动过程中，它的最大摆动角度将达到梯形斜边与垂直直线夹角的两倍以上。滑块摆动角度与后接导轨半径近似成反比，因此在满足空间要求的前提下，尽可能通过增大圆弧导轨的半径来减小滑块的摆动角度。

②滑块参数对圆弧导轨参数的影响分析

上面提到的圆弧半径R值实际上受到滑块参数的影响，梯形滑块的上下底边差距越小，滑块与圆弧导轨之间的间距就越小，其在过渡过程中的摆动角就越小。因此要使圆弧导轨的半径小一点，同时过渡过程中摆角也要小一些，则最好的办法就是使梯形上下底边差最小，同时其长度也要尽可能地短一些。如果滑道的宽度能小一些，也有利于减小圆弧轨道的半径值。但如果滑块参数的变化可能会对其所携带的负载产生比较大的影响，从负载的角度讲，滑块各方面参数应尽可能大一些为佳。

③机器运动速度对圆弧半径的影响分析

机器速度越快，滑块进入圆弧轨道后的离心力就越大，这会对传送皮带形成比较大的离心拉力，容易加速皮带疲劳损坏。由于这个离心力是周期性的，因而还会形成系统振动，当其振动固有频率与系统上的某些部件固有频率接近时，会引起系统共振。其工作频率为：

V为机器运转的速度，n为单位长度内的头数，4为环形导轨上的四段圆弧导轨。假定机器速度为18米/分，每米有3个安装手套装置，则f=6H?Z左右。这是基频频率，它还有可能会产生2次或3次谐波，从而有可能对机器工作状态产生影响。当机器的速度要求比较高时，可通过ANSYS软件分析滑块与轨道之间的接触受力状况，为滑块和导轨的强度和刚度设计提供理论依据。

④圆弧导轨和滑块的啮合分析

要使滑块在圆弧导轨上无间隙运动（如图5所示），只有梯形滑块頂边和底边完全在同心圆上。由于可以画出无数个通过四点的同心圆，所以R可以有无数个值。但当轨道的宽度确定后，R只能有唯一一个值。假定圆心的点用0表示。

其中Rh为圆弧导轨的宽度。改变Rh的值，R的值就随着改变，Rh的最大值就是梯形滑块斜边的长度。这种结果会导致圆弧导轨和直线导轨直接连接时，出现厚度不一样偏差。梯形上下底边长度差值越小，这个导轨过渡位置的偏差就越小，但导轨的半径就越大。同时又要偏差小，又要半径小是很难同时做到的。所以采用过渡曲线来连接直线导轨和圆弧导轨，这样才能保证滑块在直线运动时和曲线运动时与导轨之间的间隙最小。

上面对直线导轨与圆弧导轨对接的影响因素做了简要分析。但是要使圆弧导轨能够正常工作，还有其他因素要分析研究，如负载对象的控制精度直接影响到导轨相关参数的确定。为保证圆弧导轨长时间工作，对导轨表面的热处理和加工方法也有一些特殊要求。除此之外导轨在安装过程中还需要反复进行运转灵活性测试，确保运动过程中无卡顿和撞击现象。鉴于滑块运动过程中的离心力存在，在研磨轨道时最好研磨圆弧轨道的外侧，即始终保持圆弧轨道的内侧与梯形滑块的滚子接触。圆弧轨道外侧的修磨长度不大于梯形底边的长度。

总之直线导轨与圆弧导轨对接给滑块运动带来了很多技术难题，在高精度设计时必须对这些问题逐一研究，才能够保证滑块负载的运动精度达到规定的技术要求。本文重点讨论的是梯形滑块的运动规律，如果采用的其他滑块结构，其研究方法也与此类似。

作者单位：北京印刷学院机电工程学院 北京印刷学院智能制造实验室 北京华德液压工业集团有限责任公司

注：本论文资助基金项目：国家重点研发计划项目（2019 YFB170302）;北京市科技重大专项（Z191100009119002）

责任编辑：李倩 liqian@cprint.cn