珊瑚岛礁场地地震作用下稳定性分析研究

赵文燕 王桂萱

(大连大学土木工程技术研究与开发中心 辽宁 大连 116622)

引言

在工程地质学中，珊瑚礁被认为是一种发育于热带海洋环境中的特殊地质体，它是由地质和生物作用共同形成的陆地类型。国内外在珊瑚岛礁方面的研究日益成熟。从19世纪50年代珊瑚礁形成演化的推理过程被达尔文提出后，与珊瑚礁的相关研究不断涌现出来，围绕珊瑚礁地形地貌、结构、海平面环境[1-2]以及稳定性[3-5]等研究层出不穷。珊瑚礁开展了许多工程应用，越来越多的建筑都建在由珊瑚碎屑、珊瑚礁碎屑和钙质砂等组成的礁石平台上[6]。1940年，澳大利亚利用珊瑚礁在太平洋岛屿上修建了高速公路和飞机跑道，据报道这些设施今天仍在使用[7]；1960年，在伊朗波斯湾附近首次发现与近海石油平台稳定性有关的岩土工程问题[8]。然而，这些问题当时并没有引起广泛关注。1970年后，珊瑚礁建设方面的问题被广泛报道，引起了人们的关注，并开始对珊瑚礁的力学特性进行研究[9-12]。

珊瑚礁方面的研究之所以能够发展迅速，由于它的出现解决了陆地不足和高额的建设成本问题，就地取材，将其作为理想的填筑材料。因此，迫切需要对珊瑚礁场地稳定性相关问题进行研究，期望为未来珊瑚岛礁工程建设以及珊瑚岛礁场地稳定性研究提供些许启发和借鉴。

一、岛礁场地地震作用下稳定性问题研究现状

近些年，岛礁工程受地震灾害影响较大，故岛礁场地的地震反应问题备受关注。有关学者相继做出了一些研究成果。孙宗勋[13]等通过非线性E-v本构模型探究了永署礁地基变形情况；Guo等[14]利用GEO-SLOPE软件对地震作用下礁体的剪切变形进行模拟，借助GEO-SLOPE、FLAC等软件以及岩土工程模拟方法测评礁体稳定性可在一定程度上评判礁体稳定性；陈国兴[15]等建立珊瑚岛礁二维地震反应分析模型，对岛礁场地地震峰值加速度及规律等进行了研究；胡进军[16]等探究了南海岛礁场地地震安全性研究所涉及的关键问题进行地震波垂直入射下岛礁地震反应研究；杨笑梅[17]等研究了二维土层下的地震反应分析的时域等效线性化解法。这些研究在地震工程学和岩土工程领域里，对珊瑚岛礁场地地震作用下的反应分析研究都具有重要参考价值。然而，为做好岛礁结构工程长期的稳定和发展，还有许多的工作需要进一步深究。

二、岛礁场地地震作用下稳定性分析原理及方法

珊瑚岛礁稳定性的影响因素主要为人为因素和地质因素两类。评估珊瑚岛礁在场地地震作用下的稳定性尤其重要。重点研究地震作用下礁体边坡的稳定性问题。目前广泛应用的分析稳定性分析方法主要有：有限元分析方法、极限平衡法以及数值分析方法等。其中，应用最广的是极限平衡法和Newmark分析方法。对具体原理及方法下文做了详细介绍。

(一)基本原理

目前工程上通常采用基于Mohr-Coulomb准则的弹塑性有限元数值计算方法得出应力分布，然后采用极限平衡原理计算出最危险的滑动面和最小安全系数，评估边坡的稳定性。在计算中，通常将力和位移作为判断边坡破坏的指标。

1.安全系数的定义

通常将安全系数定义为极限应力与许用应力之比。对于物体上的任意一点，若安全系数大于1，则该点稳定；若安全系数等于1，则该点处于不稳定的关键状态；否则认为该点认为不稳定。选择安全系数Fs作为标准，其定义是将块体的抗剪强度指标(粘聚力c′和内摩擦角φ′)减少为c′/Fs和tanφ′/Fs，则块体在某一滑裂面上能够达到极限平衡状态[18]，即

(1)

(2)

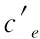
2.Mohr-Coulomb强度准则

Coulomb(库伦)公式通常表示为

(3)

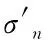
Mohr(莫尔)公式常表示为

τ=f(σ)

(4)

式中，σ为正应力。

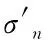
(5)

式中，α为底倾角，tanα=dy/dx；u为孔隙水压力，通常定义孔隙水压力系数为

(6)

式中，γ为平均容重，h为中线的高度；uw为正孔隙水压力。

3.静力平衡条件

若将滑动土体分成多个土条，如图1所示，在每个土条和整个滑动土体都必须满足力和力矩平衡条件。在静力平衡方程组中，未知数的个数超过了方程组的个数，解决这一不静定问题的方法是对冗余的未知数作假定，使剩下的未知数的数目等于方程组的数目，从而求出静力平衡方程的解。

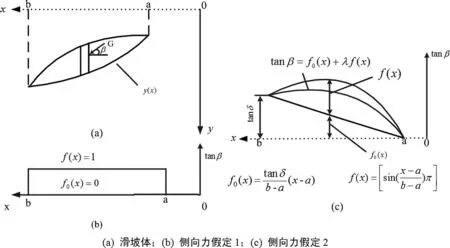
图1 边坡稳定的条分法

Fig.1 Slice method for slope stability

对于任一土条i，其受力情况如图 2所示。设想该土条沿y=y(x)下滑，分别考虑水平和垂直向上的力的平衡，建立x和y方向的静力平衡方程：

ΔTcosα-ΔNsinα-ΔQ+Δ(Gcosβ)=0

(7)

ΔNcosα+ΔTsinα-(ΔW+qΔx)+Δ(Gsinβ)=0

(8)

式中，ΔW—土条重量，浸润线上为天然容重，浸润线下为饱和容重；

qΔx—坡表面垂直荷重；

ΔQ=ηΔW—水平的地震力，其作用点与底面的垂直距离为he；

X—土条垂直面上的剪应力；

G—土条垂直边上的总作用力

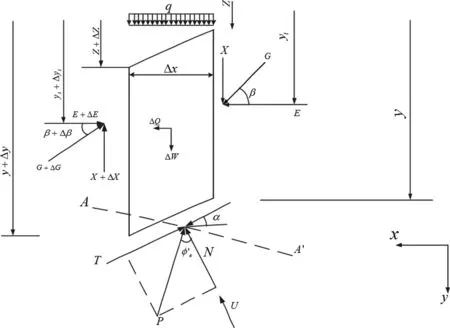
图2 任一条块的受力分析

将式(5)代入式(7)和式(8)中，消去ΔN，令Δx→0，得到静力平衡的微分方程：

(9)

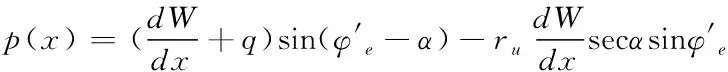
(10)

同时，将作用在土条上的力对土条底中点取距，建立力矩平衡方程：

(11)

对于静力平衡方程的解的问题，对微分方程(9)和(11)需要加入边界条件：

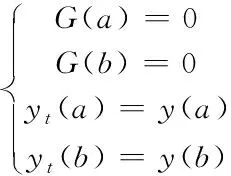
(12)

式中，a和b为滑体左、右端点的x坐标。

Morgenstern和Price假定它符合某个分布形状，留下一个待定常数λ和F一起求解，即假定tanβ=λf(x)。因此，稳定分析就转化为求解仅包含两个未知数λ和F的联立方程组的问题。通常，我们假设f(x)=常数=1，如图1(b)所示。尽管实际计算结果表明f(x)的形状对安全系数数值的影响不大，但需要β(x)在该两端为指定值以确保x=a和x=b处的剪应力成对原理不被破坏。因此，假设tanβ=f0(x)+λf(x)，则f(x)在x=a和x=b处为指定值，f0(x)在x=a和x=b处为零，如图1(c)所示，同时，对式(11)积分可以计算出土条垂直面上的有效法向应力作用点的纵坐标：

(13)

(二)极限平衡法

极限平衡法是一种已被长期的工程实践证明对岩土稳定性分析有效且相对可靠的方法。基本方法：假定边坡不稳定发生破坏时，边坡内部会产生滑动面，坡体沿滑动面滑动即造成失稳破坏。根据静力平衡原理，引入假定条件，得出了一些列的破坏荷载和最危险滑动面，从而达到定量评价的目的。

极限平衡法是建立在莫尔-库伦强度准则的基础上，其表达式为

τf=c′+σ′tanφ′=c′+(σ-u)tanφ′

(14)

式中，τf为破坏面上的剪应力；c′为土的有效粘聚力；σ和σ′为破坏面上总应力和有效法向应力；φ′为土的有效内摩擦角。

在20世纪60年代，由Morgenstern和Price提出的Morgenstern—Price法是最典型的方法，并且它是唯一一种对静力平衡要求、滑裂面的几何形状以及假定多余未知数的选择上都不做假设的方法。M-P极限平衡条分法主要将土条侧面的总水平推力E和切向力X分别替代式(7)和(8)中的Gcosβ和Gsinβ，同样消去N′后令Δx→0，得到静力平衡的微分方程：

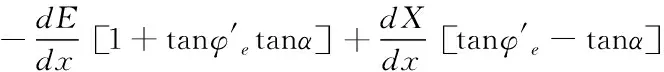
(15)

力矩平衡方程为

(16)

在求解过程中，每个土条的几何物理参数需要进行线性化：

对底滑面

y=Ax+B

(17)

对土条重量

(18)

对土条水平荷载

(19)

对式(13)中的侧向力假定为函数

f(x)=kx+m

(20)

则力矩平衡方程(16)可转化为

(21)

(22)

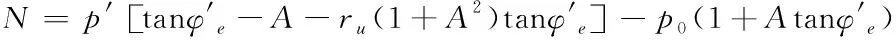
(23)

(24)

(25)

基于线性化在xt到xt+Δxt区间对方程式(21)进行积分，可以解得

(26)

从边坡顶部第一个界面E0=0开始，至上而下，逐次求出法向条间力Et，同时，最后一土条必须满足条件

En(F,λ)=0

(27)

对微分方程式(16)积分，考虑到E(a)=E(b)=0，可得

(28)

三、总结与展望

通过上述分析可知，目前，围绕影响岛礁地基稳定性的研究已取得一些成绩。然而，为做好岛礁工程结构长期稳定与运筹工作，仍需要开展大量的研究工作，为此，笔者对珊瑚岛礁地震作用下稳定性分析总结如下：

(1)极限平衡法原理简单、计算方便、易于操作，能够给出容易接受的稳定性指标，因此已广泛应用于边坡稳定性评价中。另外，基于简化的Newmark位移模型，可以快速评估该区域内的地震滑坡情况，并能够快速识别出地震滑坡的高易发区和高风险区，为地震应急响应工作提供重要的参考依据；但是，极限平衡法很难分析复杂的边坡稳定性，且求得的安全系数仅为假定滑动面上的平均安全度。目前，复杂工程较多使用的是有限元极限平衡法，即将有限元计算和极限平衡法结合起来。

(2)Newmark分析法算法简单、适用性广泛，是评估边坡地震稳定性的有效手段之一。目前应用Newmark分析方法计算地震边坡的永久位移还存在较多问题，应加深对边坡动力特性、地震反应以及地震动的模拟方面的认识。

(3)珊瑚礁在不受外力作用时是稳定的，当礁体内部受到外部应力的作用时，其应力状态将发生变化，应力出现局部集中现象，笔者建议，在岛礁上进行相关工程建设时，可以通过了解珊瑚礁现有的土工特性、地质组成、地形地貌及相关的动力因素的基础上，加固天然地基，采用应用较广的极限平衡法来礁体评估边坡稳定性。具体包括创建礁体斜坡有限元模型、滑移模式，确定礁体地层结构、土体强度、地形参数、水动力等指标，引入GEO-SLOPE软件模拟不同风浪、地震烈度的稳定性。当然，在评价珊瑚岛礁边坡稳定性时，考虑到波浪可增加土体的孔隙水压力，而潮汐可增强土体内孔隙水的渗流力，由于这些因素的影响，研究还需要分析其产生的应力值，例如对所研究的礁体相应区域的底床土进行适当的土工试验，结合相应的解析表达式和软件数值模拟等进行计算与分析。最终，通过上述仿真模拟及实验得出的结果，可以预测出礁体稳定性的变化趋势，从而确定礁体发生失稳破坏的可能性。