高强矩形螺旋钢筋约束高强混凝土剪力墙截面弯矩-曲率计算方法研究
2020-09-17赵花静李青宁李书锋
赵花静,李青宁,赵 珺,李书锋,郑 玉
(1. 西安建筑科技大学理学院,陕西,西安 710055;2. 西安建筑科技大学土木工程学院,陕西,西安 710055;3. 许昌学院交通运输学院,河南,许昌 461000)
剪力墙墙肢的塑性变形能力和抗地震倒塌能力,除了与纵筋配筋率、截面相对受压区高度或轴压比有关外,还与墙体采用的混凝土材料[1]、两端的约束范围、约束区配箍特征值及配箍形式等有关[2]。通常在剪力墙两端设置约束边缘构件,使墙肢端部成为箍筋约束混凝土,从而具有较大的受压变形能力[3]。因为高强矩形螺旋箍筋所具有的高强、连续、封闭的特点,已被广泛应用于梁、柱、节点等构件[4−5]。本文将其应用到高强混凝土剪力墙约束边缘构件中,能够显著提高约束混凝土的极限压应变,从而有效提高高强混凝土剪力墙的承载能力和变形能力。
本文基于10 片HRSR 高强混凝土剪力墙的低周往复加载试验结果,拟对考虑边缘构件约束混凝土影响的HRSR 高强混凝土剪力墙截面弯矩-曲率分析法[6]进行研究;以开裂点、屈服点、峰值点和极限破坏点为特征点,将实际的弯矩-曲率曲线简化为4 线型骨架曲线模型[7];基于试验中剪力墙截面应变的实际分布,分别建立HRSR 高强混凝土剪力墙开裂状态、屈服状态、峰值状态、极限破坏状态时的弯矩-曲率计算方法,推导了各状态弯矩和曲率的表达式。
1 试验概况
1.1 试件设计
对两组共10 个1/2 缩尺模型—HRSR 高强混凝土剪力墙试件[8−9]进行了拟静力试验。墙体截面两端设置约束边缘构件,纵筋采用HRB400 级热轧钢筋。箍筋和水平分布筋采用直径为5 mm的HTH1000 高强度热处理钢筋[10],以嵌套方式配置,形成高强矩形螺旋箍筋和高强螺旋水平分布筋。试件几何尺寸及配筋见图1。主要参数详见表1。混凝土及钢筋的力学性能指标见表2 和表3。
1.2 加载装置与加载制度
试验拟静力加载装置如图2 所示。加载制度同文献[8]。
1.3 测试内容及测点布置
试验中主要测试内容有:1) 墙顶水平荷载和位移;2) 墙体塑性铰区弯曲变形、钢筋滑移变形以及总水平位移;3)墙体塑性铰区以上区域剪切变形;4) 梁的刚体位移;5) 墙体塑性铰区纵筋及竖向分布筋应变;6) 荷载-位移滞回曲线。位移计布置如图3 所示。
2 本构关系

本文采用的高强箍筋约束高强混凝土应力-应变全曲线[11],如图4 所示。该模型的上升段和下降段分别采用Popovics 模型[12]和Fafitis 和Shah 模型[13]的表达形式。因本文与文献[11]所采用的为同一批高强矩形螺旋钢筋,且通过对峰值状态时的剪力墙约束区应变试算比较符合,因此采用该本构模型。

图1 试件几何尺寸及配筋 /mm Fig. 1 Dimensions and reinforcements arrangement of specimen
其具体表达式如下:

式中:fcc与 εcc分别为约束混凝土的峰值应力和峰值应变;fc0与 εc0分别为非约束混凝土的峰值应力和峰值应变,取 εc0=0.002[8];fc与 εc分别为墙身混凝土的抗压强度及对应的应变; α为控制曲线初始刚度和上升段的系数, α值越大,表明上升段越接近直线且弹性模量越大。 ε85与 ε085分别为约束与非约束混凝土强度下降至峰值的85%时所对应的应变[11];fle为约束混凝土达到峰值应力时对应的箍筋有效侧向约束力[14]; ρsv为面积配箍率。
3 骨架曲线
取低周反复水平荷载作用下剪力墙试件P-Δ滞回曲线的外包线得其骨架曲线,将其简化为4 线 型,如 图5 所 示。图 中Mcr、φcr、My、φy、Mp、φp、Mu、φu分别表示开裂点、屈服点、峰值点和极限破坏点对应的弯矩和曲率[7]。
4 HRSR 高强混凝土剪力墙正截面弯矩-曲率方程
针对以弯压破坏为主的HRSR 高强混凝土剪力墙构件,考虑其边缘构件高强螺旋箍筋对混凝土的约束作用,分析轴力N和弯矩M共同作用下的偏心受压计算,提出对称配筋的HRSR 高强混凝土剪力墙各阶段正截面弯矩-曲率的计算方法。
4.1 开裂弯矩和曲率
图6 为实测的HRSR 高强混凝土剪力墙开裂点截面应变分布图。当剪力墙截面受拉区边缘混凝土应变达到其极限拉应变 εtu时,受拉区混凝土开裂,剪力墙截面进入开裂状态,对应的开裂弯矩为Mcr。

表1 试件主要参数Table 1 Parameters of specimens
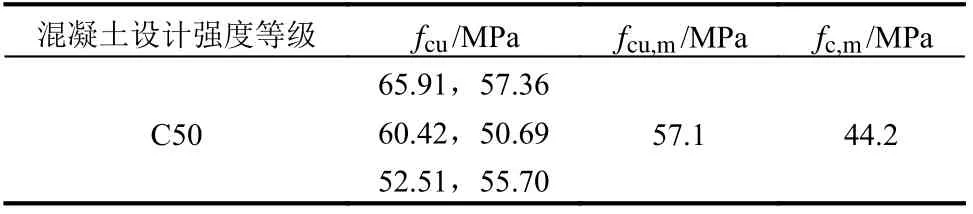
表2 混凝土力学性能指标Table 2 The mechanical properties of concrete
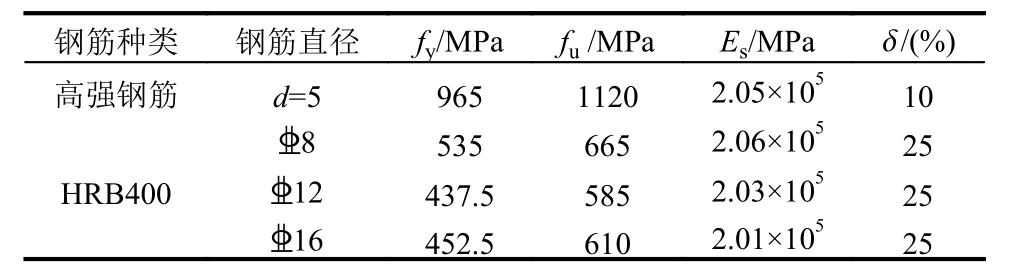
表3 钢筋力学性能指标Table 3 The mechanical properties of reinforcements

图2 试验装置图Fig. 2 Test set-up
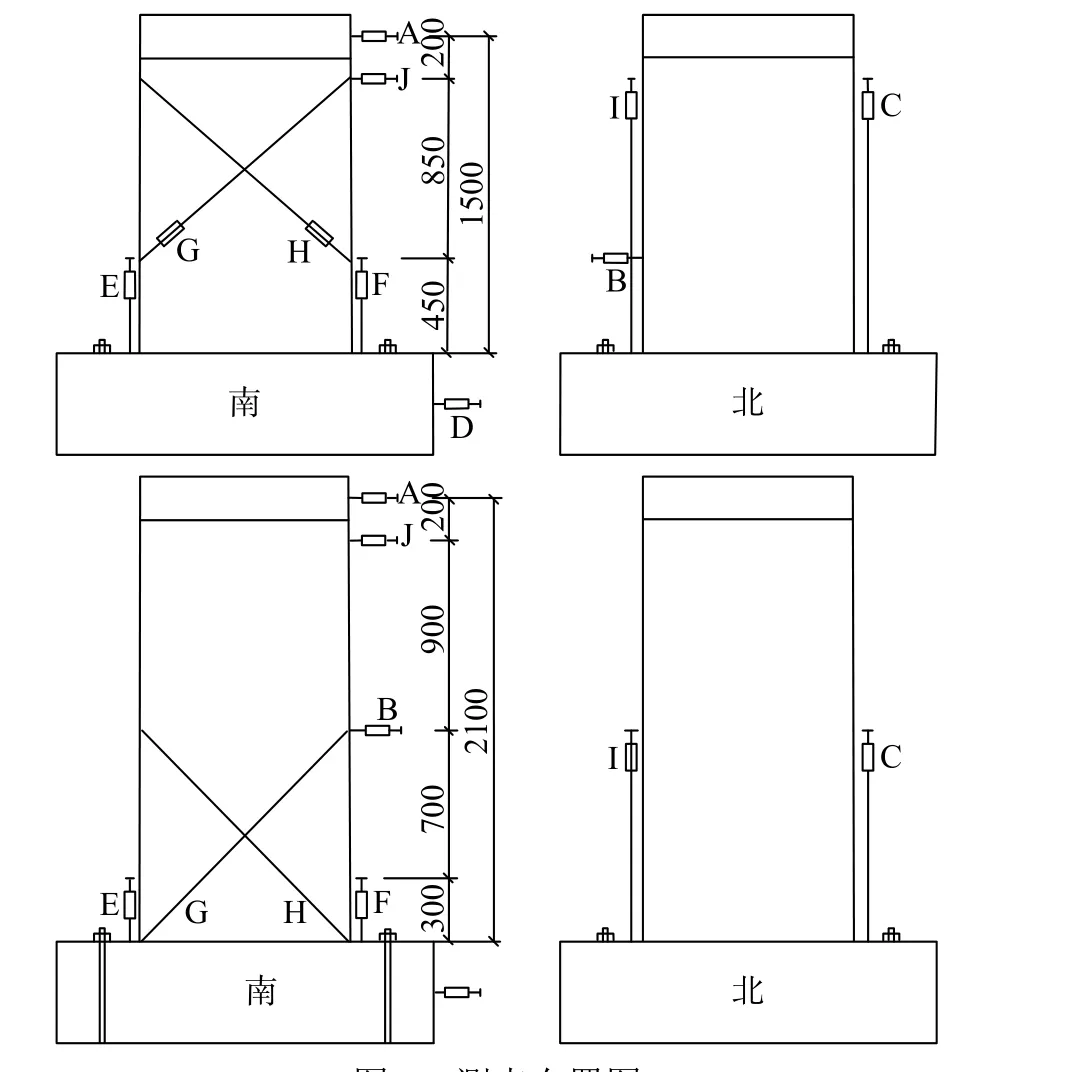
图3 测点布置图 /mm Fig. 3 Displacement measuring point arrangement

图4 应力-应变全曲线Fig. 4 Stress-strain curve
该阶段基本特点为:1)剪力墙截面受拉区边缘混凝土达到其极限拉应变 εtu,截面受拉区混凝土应力呈曲线分布,为简化计算,按照开裂弯矩相等的原则,将受拉区曲线应力图转换为三角形分布图[15],其最外边缘混凝土应力取 γft, γ=2.0;2)截面受压区混凝土应力仍处于弹性阶段,压应力图形为三角形分布;此时螺旋箍筋的拉应力很小,对核心混凝土的约束作用不明显,因此不考虑高强螺旋箍筋约束作用;3)考虑约束边缘构件中受拉和受压纵筋的作用;4)竖向分布筋应力按三角形分布计算;若其配筋率较小时,可忽略其作用。
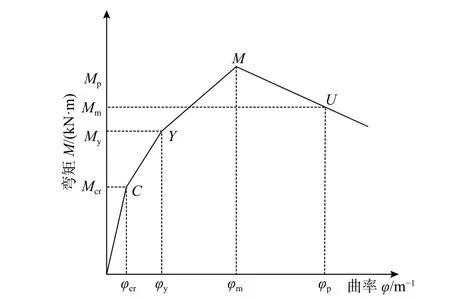
图5 弯矩-曲率骨架曲线Fig. 5 Moment-curvature skeleton curve
根据上述分析,可得图7 所示剪力墙开裂截面的应力、应变分布。由图7 所示截面应变图,可得截面开裂曲率,即:

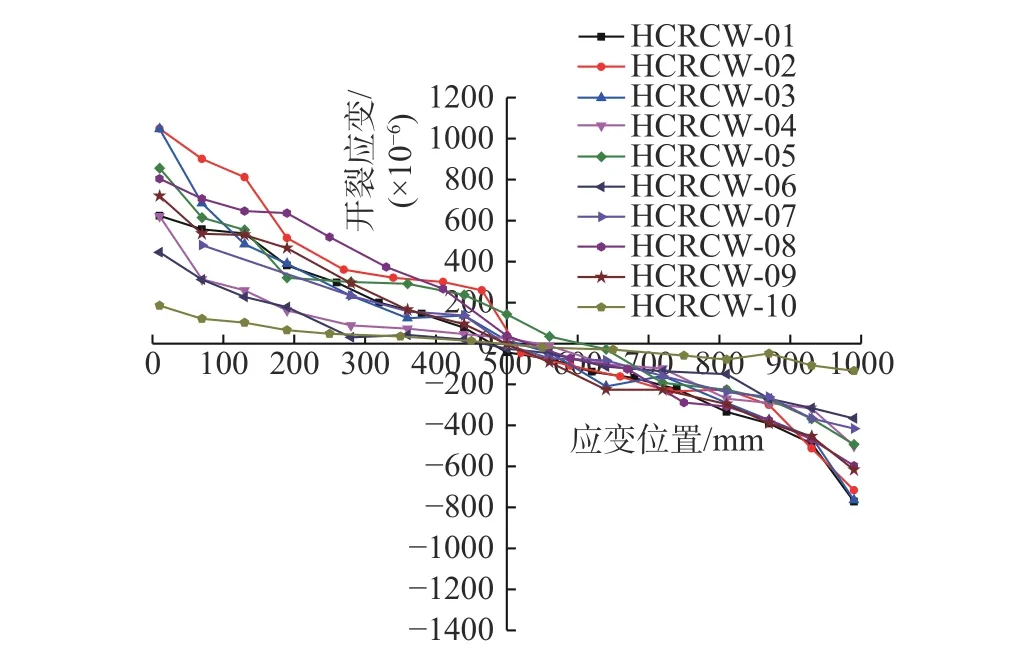
图6 实测开裂状态截面应变分布图Fig. 6 Measured strain distribution of section at cracking state

图7 截面开裂状态应力、应变分布图Fig. 7 Stress and strain distribution of section at cracking state


4.2 屈服弯矩与曲率
图8 为实测HRSR 高强混凝土剪力墙屈服点截面应变分布图。可以看出,截面屈服时受拉区纵向受力钢筋应变已达到其屈服应变,且实测平均应变沿墙截面高度的变化规律仍能基本符合平截面假定。所有试件在截面受拉区边缘出现应变突增,主要原因是受剪切变形的影响;其中试件HCRCW-01、HCRCW-02 和HCRCW-07 在截面中心区域竖向受拉分布筋出现应力突然增大,应变加快。原因在于该处有斜裂缝穿过,导致钢筋应力增长。总体而言,截面应变仍然满足平截面假定。

图8 实测的屈服状态截面应变分布图Fig. 8 Measured strain distribution of section at yielding state

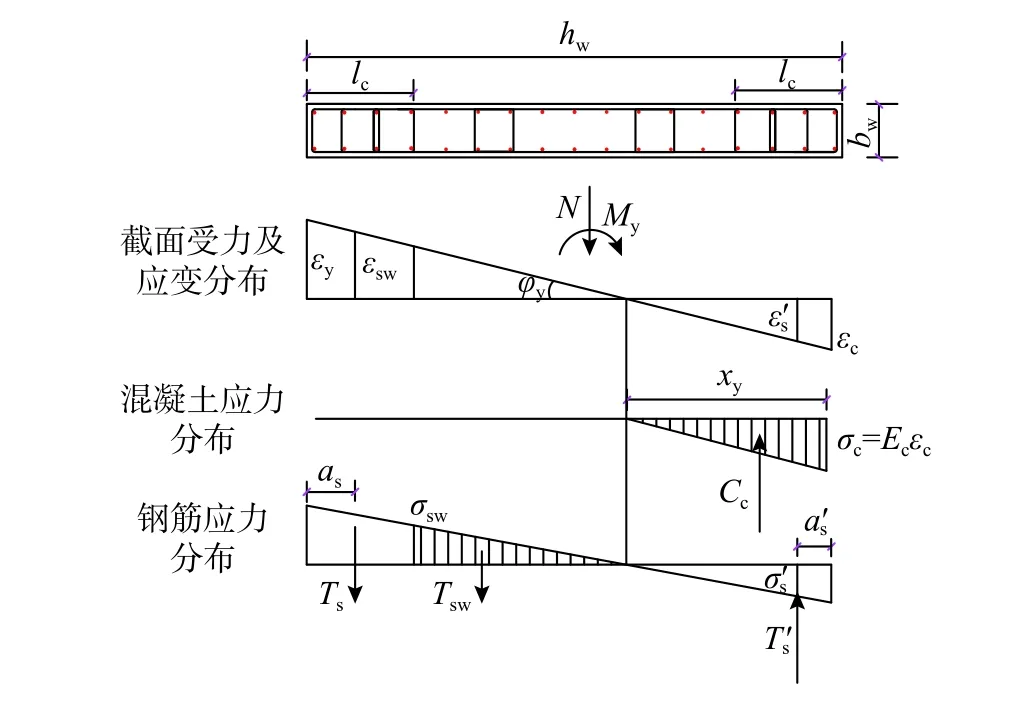
图9 截面屈服状态应力、应变分布图Fig. 9 Stress and strain distribution ofsection at yielding state

4.3 峰值弯矩与曲率
试验表明[8−9],剪力墙边缘构件设置高强螺旋箍筋可提高其极限承载力及变形能力,因此计算时应考虑高强螺旋箍筋对核心区混凝土的约束作用[16]。图10 为实测HRSR 高强混凝土剪力墙峰值荷载点截面应变分布图。可以看出,截面受压区约束边缘构件应变出现大幅度增长,截面应变不再符合平截面假定。由图10 可知,从截面受拉端至非约束区受压外侧应变分布为线性分布,截面受压侧约束边缘构件应变梯度增大[17]。依据峰值荷载状态实测应变,HRSR 高强混凝土剪力墙达到峰值荷载时,约束区截面外侧(扣除混凝土保护层)受压应变平均值为13892×10−6,非约束区受压外侧平均应变为2980×10−6,达到了非约束混凝土的极限压应变。

图10 峰值状态截面应变分布图Fig. 10 Measured strain distribution ofsection at peaking state
本文提出高强螺旋钢筋约束高强混凝土剪力墙截面峰值状态承载力计算简图如图11 所示,当截面受压外侧达到约束混凝土的极限压应变εccu(取应力下降至峰值应力85%时对应的应变 ε85),非约束区受压外侧应变达到混凝土极限压应变εcu( εcu=0.003)时,剪力墙截面达到最大承载能力,此时对应的峰值弯矩为Mp。
该阶段的基本特点为:1)墙体屈服后,截面受拉区与受压区应变分布不再符合平截面假定,主要由于粘结滑移影响而导致[18];2)不考虑受拉混凝土的作用;受压区非约束区混凝土应力达到fc,约束混凝土内侧应力达到峰值应力fcc[11],约束混凝土外边缘应力约为峰值应力的0.85 倍,即受压区约束混凝土应力取峰值应力fcc下降至0.85fcc的直线;3)在峰值荷载状态下,拉、压约束边缘构件纵向钢筋应力均已达到极限抗拉强度fs=fu(用于设计计算时取fs=fy);4)达到峰值承载力时,墙体水平分布筋未达到屈服,受压区竖向分布筋尚未屈服,不予考虑。只考虑竖向分布钢筋受拉作用。
竖向分布筋屈服强度较高(fyw=965 MPa),当剪力墙达到峰值荷载时,靠近约束边缘构件的竖向分布筋能达到屈服强度,受拉应变平均值为4765×10−6,靠近形心轴的受拉应变平均值为1660×10−6,根据试验中应变的实际大小及分布,规定受拉区竖向分布筋应力呈三角形分布。
因非约束区混凝土应力呈曲线分布,用等效矩形应力图代替实际的混凝土压应力图形,等效矩形应力图形高度为压区实际高度的0.8 倍[13,18−19]。
约束区混凝土采用文献[11]的高强箍筋约束高强混凝土应力-应变关系,非约束区混凝土采用文献[15]的应力-应变关系。
1)当x>lc时(即受压区高度大于约束区长度时),如图11(a)所示,可得截面的峰值曲率,即
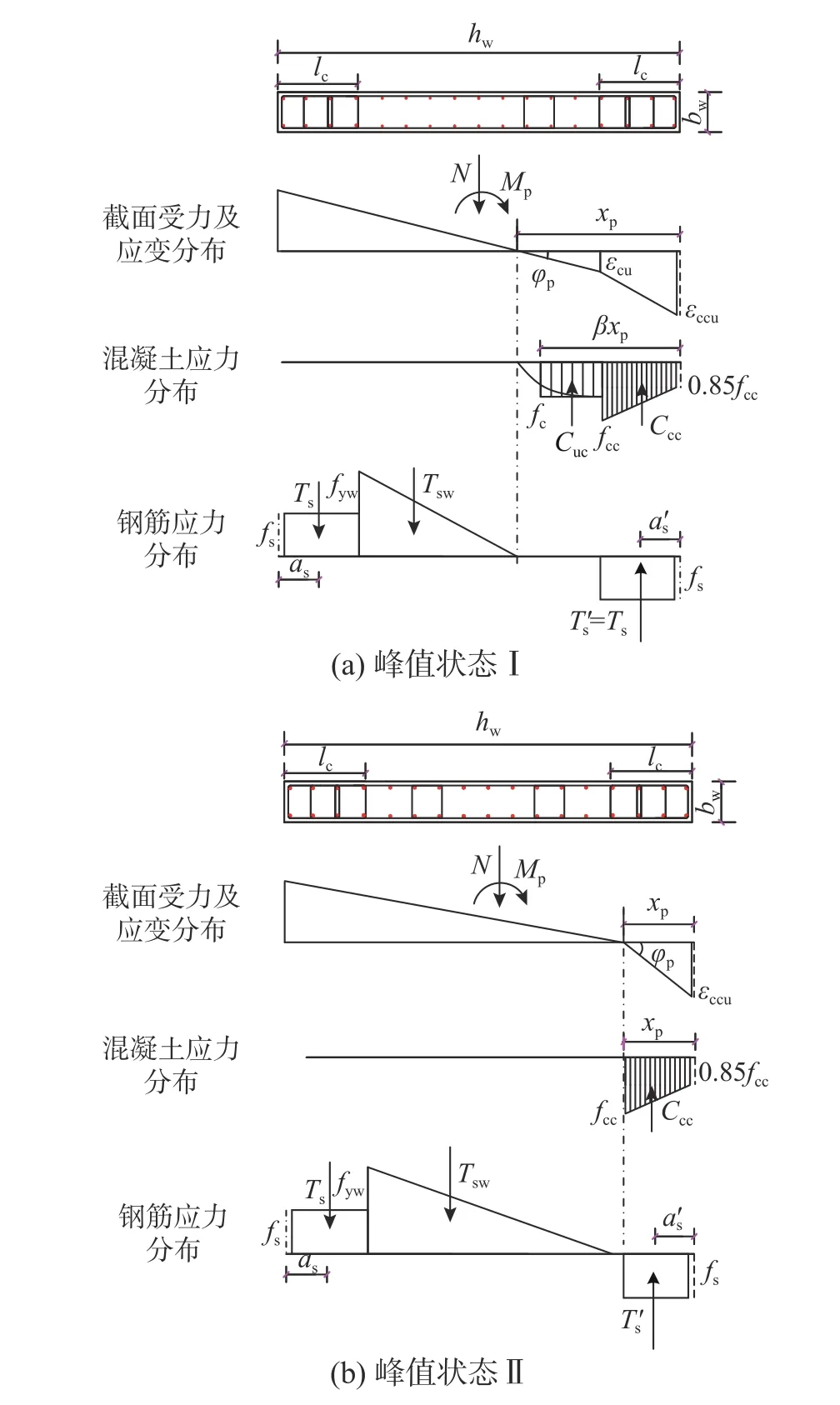
图11 截面峰值状态应力、应变分布图Fig. 11 Stress and strain distribution of wall at peaking state

式中, εcu为非约束混凝土极限压应变,取εcu=0.003;xp为峰值状态下剪力墙截面受压区高度;lc为剪力墙约束区高度。
截面各力的关系式如下:
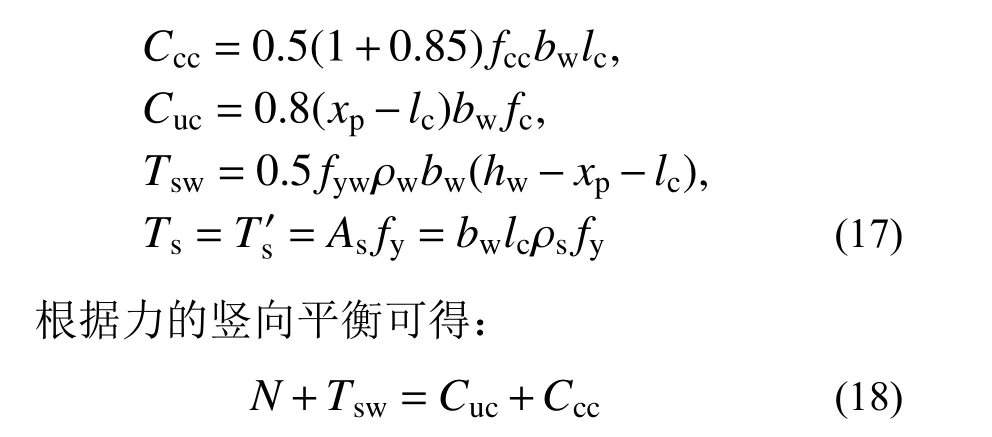
对形心轴取矩,截面峰值弯矩为:

其中:

联立式(16)~式(20)可求得xp和Mp。
2)当x 截面各力的关系式如下: 根据力的竖向平衡可得: 对形心轴取矩,截面峰值弯矩为: 当剪力墙承载力降到85%峰值荷载时,受压区约束混凝土应变达到相应的极限压应变 εccu。此时,HRSR 混凝土剪力墙达到破坏状态。该阶段截面应变不再符合平截面假定。受拉纵筋均达到极限抗拉强度甚至可能发生断裂,受压区混凝土被压碎。达到破坏状态时,破坏弯矩Mu=0.85Mp,εccu取约束混凝土强度下降至峰值强度的65%时所对应的应变[11],即: 破坏曲率φu为截面边缘压应变达到 εccu对应的曲率,即: 试验表明,当截面边缘混凝土压应变达到混凝土峰值应变后,截面受压区高度基本保持不变[7,18],因此计算破坏曲率时可取受压区高度xu=xp。 表4 和表5 分别列出了10 个HRSR 混凝土剪力墙开裂点、屈服点以及峰值点时水平承载力的计算值与试验值,其中试件HCRCW-04 在塑性铰区加有槽钢,HCRCW-08 和HCRCW-09 分别在剪力墙塑性铰区和墙身外套螺旋钢筋,因此这三个试件计算结果与试验结果相比均偏小,误差较大。在后面的结果分析中,剔除这三个试件的影响。 表4 开裂、屈服荷载计算值与试验值的比较Table 4 Comparison between calculated values and test values of cracking and yielding loads 由表4 结果可知,开裂状态误差较大。因试件加载时,通过肉眼判断其产生裂缝为开裂状态,这种方法并不精确,裂缝可能产生在加载过程中,观察具有滞后性,且高强螺旋箍筋的约束作用,也能提高开裂荷载,计算时未考虑这部分作用,因此导致计算值偏小。 从表4 可以看出,试件HCRCW-01 开裂荷载较大,说明开裂荷载随着轴压比的增大而提高。开裂荷载计算值与试验值比值的平均值为0.873,标准差为0.101,变异系数为0.115。计算结果偏于安全。由表4 可以看出,屈服荷载计算值与试验值相比,基本吻合。其中试件HCRCW-06 和HCRCW-07 计算值偏大,主要因为其纵筋配筋率过大,并未全部达到屈服,计算时过高估计了纵筋的贡献。屈服荷载计算值与试验值比值的平均值为0.959,标准差为0.0385,变异系数为0.040。 分别按照fs=fu和fs=fy两种方法计算HRSR剪力墙的峰值荷载,结果见表5。图11 是按照HRSR高强混凝土剪力墙截面应变分布实测值进行简化而得,结果证明,计算的峰值荷载计算值与试验值比值的平均值为1.024,标准差为0.038,变异系数为0.037。从表5 可以看出,当纵筋的强度取极限抗拉强度时,即fs=fu时,峰值荷载吻合良好,这与试验现象是相符的,因试件达到峰值荷载时纵向受力钢筋已达到了极限抗拉强度。当进行试件设计时,应采用fs=fy,至少有10%的安全储备。可以看出,采用高强矩形螺旋钢筋约束的高强混凝土剪力墙能够充分发挥纵筋的抗拉强度以及混凝土的抗压强度,达到较高的承载力,表明本文建议的峰值荷载计算公式较为合理。 表5 峰值荷载计算值与试验值的比较Table 5 Comparison between calculated values and test values of peaking load 表6 列出了HRSR 高强混凝土剪力墙各阶段曲率的计算值与试验值,对比结果可知,曲率计算值与试验值偏差较大,尤其是开裂状态。主要原因是开裂荷载无法精确判定所导致。试件HCRCW-04 因在塑性铰区加有槽钢,试验时未监测塑性铰区的弯曲变形。试件HCRCW-08 因塑性铰区加有外套螺旋钢筋,试验值与计算值差别较大。从表6中可以看出,试件达到屈服荷载前,曲率随着轴压比的增加而逐渐增大;达到屈服荷载后,曲率随着轴压比的增加而逐渐减小。 表6 截面曲率计算值与试验值的比较Table 6 Comparison between calculated values and test values of curvature 本文通过对10 片HRSR 高强混凝土剪力墙试件的拟静力试验研究与理论分析,得出以下结论: (1)基于HRSR 对高强混凝土的约束作用,且根据试件截面应变分布实测值,利用四折线模型,建立HRSR 高强混凝土剪力墙开裂、屈服、峰值和极限破坏状态对应的弯矩-曲率计算方法。通过与试验结果比较,其计算值与试验值吻合较好,表明本文建议的方法较为合理。 (2)采用HRSR 约束的高强混凝土剪力墙,能够充分发挥纵筋的抗拉强度以及混凝土的抗压强度,达到较高的承载力。约束边缘构件采用的高强连续封闭螺旋箍筋,在达到承载能力极限状态时核心区混凝土全部达到约束混凝土抗压强度,因此计算时应采用约束混凝土本构关系。 (3)计算结果表明,HRSR 高强混凝土剪力墙塑性铰区外套高强矩形螺旋钢筋可以提高其承载力和变形能力,本文在计算时,未考虑该部分作用,因此导致试件HCRCW-08 和HCRCW-09 计算值偏小。在后续研究中,应进一步考虑该部分作用。



4.4 破坏弯矩与曲率
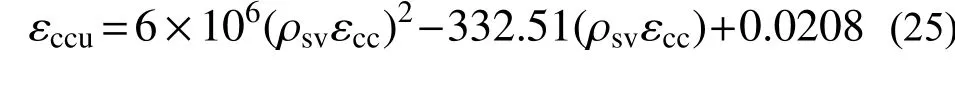

5 计算结果与试验结果对比分析



6 结论
