高职院校工程数学课程改革实证研究

2020-09-17谢旭华

石家庄职业技术学院学报 2020年4期

牛铭，谢旭华

(石家庄职业技术学院机电工程系,河北石家庄 050081)

党的十九大从新时代坚持和发展中国特色社会主义的战略高度，作出了优先发展教育事业，加快教育现代化，建设教育强国的重大部署.教育信息化是教育现代化的特征之一.信息技术在教育中的应用正在引起一场教育革命，如教育观念、教育过程、教育模式、教师角色等发生了一系列的变化.这场变革以“提高教师应用信息技术水平，更新教学观念，改进教学方法，提高教学效果；鼓励学生利用信息手段主动学习、自主学习，增强运用信息技术分析问题、解决问题的能力”[1]为教育教学改革的重点.

工程数学是高职院校理工类各专业的一门重要基础课，为后续工程技术类专业课的学习提供必需的数学基础知识和用数学知识解决工程实际问题的能力.此课程的特点是内容多而抽象，学时少，尤其是线性代数部分，在具有独特的程序化计算特征的同时，又具有枯燥的、繁琐的数值计算的特点，而这正好是计算机的专长.如何利用计算机培养学生的学习兴趣、数学素质和能力，应是高职院校工程数学课程改革的方向之一.钱学森先生在1989年曾说：“现在已经可以看到电子计算机对工程技术工作的影响，今后对一个问题求解可以全部让电子计算机去干，不需要人去一点一点算.而直到今天，理工科大学一二年级的数学课是构筑在人自己去算这一要求上的.所以理工科的数学课必须改革，数学课不是为了学生学会自己去求解，而是为了学生学会让电子计算机去求解，学会理解电子计算机给出的答案，知其所以然，这就是理工科教学改革的部分内容.”[2]因此，在现代教育背景下，对高职院校的工程数学课程进行改革，让学生学会用电子计算机去求解问题，学会理解电子计算机给出的答案，就显得非常重要和必要.

1 工程数学课程教学中存在的主要问题

(1)注重手工运算能力的培养，缺乏对大数据处理能力的培养

目前，工程数学课程教学解决的主要是运算能力问题，也就是教给学生会运算，且以手工运算为主，计算机运算较少，对这种计算问题，利用计算机则可以快速解决.而培养学生用计算机进行大数据处理的能力，不借助于数学软件的传统教学方式是无法实现的.大学生是网络化生存和电子化生活的一代，他们对电脑及软件的使用比较感兴趣.而对传统手工运算，学生相对兴趣较低且错误率较高.针对学生喜欢电脑和工程数学课程的特点，用电脑软件可以很好地解决工程数学的数值计算问题，也可以提高学生学习工程数学的兴趣和数据处理能力.

(2)理论与实际联系不够紧密

教师教学时，大多单纯从数学角度讲解课程内容，与学生的专业知识和生活实际联系不紧密，且忽视学生所学专业的差异，导致教师重理论，学生重结果，缺乏将工程数学转化为相关数学模型，进而应用于生活中解决实际问题的能力.

(3)课程考核内容相对单一

工程数学课程的考核以考查概念和手工运算技巧为主，很少涉及开放性的数学应用问题.这容易让学生认为工程数学就是做题，而这与现代教育背景下高职人才的培养应走“实用型”这一教育思想相悖.

2 工程数学课程改革的实证研究

本文采用实证研究的方法，以石家庄职业技术学院2018级机械制造专业与机电一体化专业两个教学班分别作为实验班和对照班，选取工程数学课程中的线性代数部分作为实验教学内容，由同一名教师分别对两个教学班进行授课，授课时间一致，授课学时相等.在实验班采取将MATLAB软件的使用与线性代数的内容融合在一起的、理实一体的教学模式组织教学，并对教学内容的编排进行了适当调整，突出了矩阵运算的应用和线性方程组的应用部分.在对照班，不采用MATLAB软件教学，仍采用原有的组织形式和内容进行教学.

矩阵乘法是线性代数部分较难理解的内容，直接给出矩阵乘法的运算法则学生不易理解.为了让学生更容易理解它，可以从学生熟悉的问题出发引导学生发现矩阵乘法的运算法则，具体方法为，给出几个学生各部分的成绩(见表1)，问当平时成绩占20%，期中成绩占30%，期末成绩占50%时，每个同学的总成绩是多少？当平时成绩占30%，期中成绩占30%，期末成绩占40%时，每个同学的总成绩是多少？

表1 部分学生成绩表 /分

让学生单独计算每个人的总成绩均没有问题，但要用矩阵描述上述问题，学生就会不知所措.为此，首先，引导学生将成绩表、各项成绩的占比和计算出来的总成绩分别用矩阵A，B和C表示.即

A，B，C的关系可以表示为C=AB，即C就是A与B的乘积.学生回顾自己的运算过程，在教师的引导下，探索出矩阵乘法的条件与运算法则.其次，教师再次强调矩阵是数据的一种存储形式，给出矩阵乘法的MATLAB程序指令，让学生上机练习使用MATLAB进行矩阵乘法运算，并给出一个班几十名学生的各项成绩，让学生计算每个学生的总成绩，使学生感受到MATLAB在大量数据运算中的优势.对照班的学生在矩阵乘法运算法则讨论结束后，给出几个低阶的矩阵乘法习题作为课后练习.

通过此例达到了两个目的：一是让学生进一步理解矩阵，学会用矩阵表示数据，理解矩阵是数据的一种存储形式；二是让学生理解矩阵乘法的运算法则，不产生直接给出矩阵乘法运算法则的唐突感.

在期末考试的内容上也进行了改革，除传统的概念识别与行列式、矩阵运算外，还增加了应用性问题，用于考察学生对矩阵的理解与应用.如其中一个考题为：

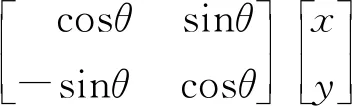
实验班用矩阵运算解答此题的占60%，求解过程如下：

而对照班只有约20%的学生解出此题，还都是一个点一个点求出的，求解过程如下：

显然，实验班和对照班的部分学生基本掌握了矩阵乘法的运算法则，但对照班对矩阵作为数据的一种存储形式的理解不如实验班到位.通过此题的解答可以看出，实验班的部分学生初步具备了用计算机进行大数据处理的能力(数据的矩阵表示是用计算机进行大数据处理的具体表现).另外，在考试中，对照班有1/4的学生将矩阵写成了行列式的形式，甚至还有学生将矩阵作为行列式进行计算，这种现象在历届学生中都有发生(虽然教师在课堂与作业中反复强调行列式与矩阵的区别)，而这种现象在实验班没有发生.原因在于，使用MATLAB软件录入矩阵时格式很严格，稍有错误系统就会提示，程序无法运行，所以实验班的学生受到了一定的严格训练，对格式比较注意.这也反映出增加MATLAB软件的学习有助于学生学习与理解矩阵的概念.

3 数据的统计分析

课程结束进行测试的内容仍然为传统教学内容，没有上机题目.对使用MATLAB软件教学的效果主要从问卷访谈和学生的上机情况来了解.在总学时不变的条件下，实验班增加10学时(5次)上机学习MATLAB软件，传统理论教学学时则减少28%.对期末考试成绩用Excel进行数据统计分析，并分别对期末考试的卷面总平均成绩和第四题(应用题)进行了F-双样本方差检验，结果见表2-3.