椭圆弧形金属阻尼器的设计与性能研究*
2020-09-17赵毛毛
赵毛毛,张 扬
(1.西安陕鼓动力股份有限公司,陕西 西安 710075;2.西安金叶电力科技有限公司,陕西 西安 710079)
0 引 言
金属阻尼器又称为弹塑度钢阻尼器或钢滞变阻尼器,是利用金属材料进入塑性状态后具有良好的滞回特性并能吸收大量能量的原理制造的一种减震耗能装置。该类装置于1972年由J.M.Kelly[1]等人提出,因其具有阻尼性能稳定、制造成本低、易于安装维护等特点,在工程建设领域得到了广泛的应用。
研究表明,金属阻尼器可有效抑制建筑结构在地震载荷下的动力响应[2-5],减小地震对结构的破坏,最大限度的保证建筑设施和人员的安全,是一种非常有效的减震耗能装置。金属阻尼器根据受力和作用方式分为扭转型、弯曲型、剪切型和拉压型等几种类型。国内外学者就如何提高金属阻尼器阻尼特性,如何有效控制设计参数等问题进行了大量的理论研究与实验验证。吴成亮[6]等人利用能量法建立了圆弧形及弓形金属阻尼器的屈服位移计算公式,并通过仿真和试验分别验证了理论计算的准确性,同时提出了对应的双线性力学模型的和经验参数取值。KazemGhabraie[7]等人利用拓扑优化算法对钢格栅式金属阻尼器的外形轮廓进行了优化,在有效降低应力集中系数和材料成本的同时提高了阻尼比。李钢[4]和晏晓彤[8]等人利用有限元仿真工具对菱形、X形及椭圆形等不同形式的开孔阻尼器进行了耗能分析,结果表明阻尼器的开口形状对其性能有较大影响,因此形状轮廓的优化对金属阻尼器的设计意义重大。
近年来,C型金属阻尼器在公路桥梁构件上得到了大量应用并取得了良好的使用效果[9-10],吴成亮[6]等人对该C型阻尼器的设计算法进行了研究,但仅限于圆弧形结构,对于沈朝勇[10]等人研究的椭圆弧形结构无法进行有效计算。笔者将在C型金属阻尼器研究的基础上,提出椭圆弧形金属阻尼器的设计方法,利用等刚度原理对其设计算法进行理论推导,并通过有限元仿真对该设计算法的有效性进行验证。
1 结构及数学模型
1.1 阻尼器结构
椭圆弧形软钢阻尼器与文献[6]所述的弧形钢阻尼器相似,都利用弧形金属臂的弯曲变形实现阻尼耗能,两者区别在于外形曲线不同,前者为椭圆线见图1(b)、(c),后者为圆弧线见图1(a)。采用椭圆线,一方面可以更好的研究形状轮廓对阻尼参数的影响,获得最佳的设计参数;另一方面受安装空间及形状尺寸等条件的约束,椭圆形阻尼器往往更符合工程使用要求。
金属阻尼器是利用材料的滞回效应来吸收能量的,塑性变形区域越大耗能效果越理想,因此在设计过程中要尽可能的保证应力和应变的均匀分布,使阻尼器有更多的面积参与塑性变形,提高阻尼器的工作效率。为了达到上述目的,在设计过程中可根据各截面受力大小来调整截面宽度,将阻尼器设计为图1(b)、(c)所示的变截面形式。

图1 弧形软钢阻尼器的元件结构
1.2 数学模型
以阻尼器中心线为研究对象对模型进行简化,具体如图2所示。
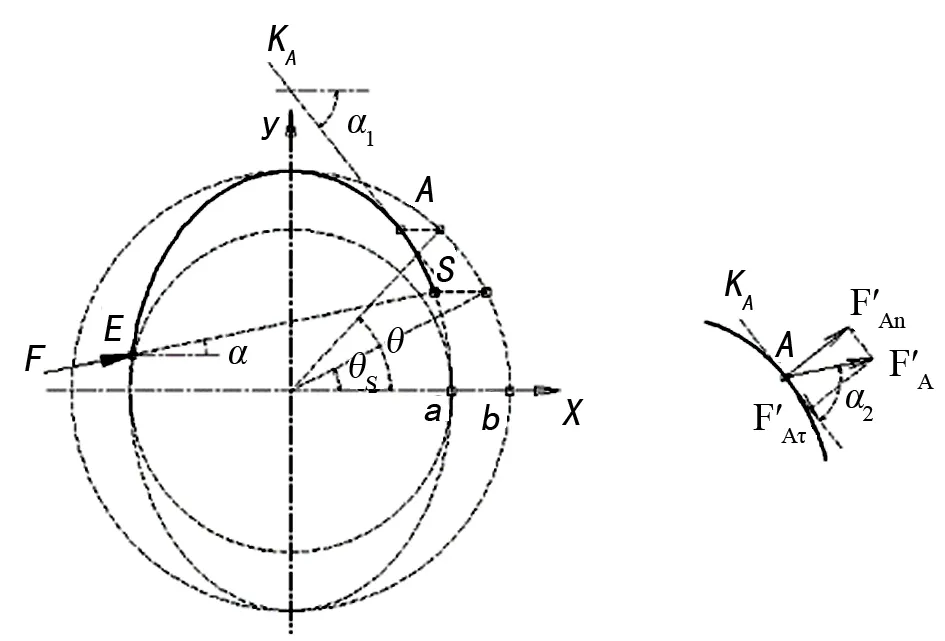
图2 阻尼器力学模型
通过以上数学模型可以推导出挤压力F作用下阻尼器上任意一点A处所受的弯矩及内力大小,进而采用材料力学原理即可得出阻尼器上任意一点的应力状态。
2 设计计算
2.1 设计强度验算
阻尼器外形尺寸确定的情况下,可利用应力计算公式对产品的强度进行校核。
tanα·X-Y+b·sinθS-α·tanα·cosθS=0
(1)
设A点到直线ES的距离为L,则L可表示为:
(2)
在已知外力F作用下,阻尼器A点处产生的弯矩为:
(3)
根据力学模型,A点处的反力FA′与外力F大小相等、方向相反。设过A点的切线及直线ES的斜率分别为kA、kES,则夹角α2可表示为:
(4)
分析可知,阻尼器各截面应力最大的点出现在内、外边缘,若阻尼器截面为矩形,截面宽度为Hθ,阻尼器厚度为B,则对应的应力大小分别为:
(5)
(6)
式中:WA为抗弯截面系数,对于矩形截面WA为:
式中:SA为截面面积,SA=BHθ;FAτ′为FA′为的切向分量,由下式计算:
FAτ′=F·cosα2
FAn′为FA′的法向分量,由下式计算:
FAn′=F·sinα2
根据第四强度理论:
(7)
截面宽度Hθ和厚度B已知的情况下,通过式(5)和式(6)即可分别得出任意截面危险点的正应力和切应力数值,通过式(7)可进行设计强度的校核。
2.2 截面宽度设计
采用等刚度原理,将阻尼器设计为变截面的形式,可以有效改善阻尼器受力情况,使各截面同时进入塑性状态,提高材料利用率并增大阻尼比。本节将采用等刚度原理,对阻尼器截面宽度计算公式进行推导。
通常,阻尼器的曲率半径与截面宽度之比远大于5,弯曲应力远大于正应力和剪应力,在计算过程中可以不考虑轴力和剪力的影响[11]。因此,为了简化计算,后续的公式推导过程均不考虑轴力和剪力的影响。
将(2)式中的L对θ求导并令Lθ′=0,可得L最大时对应的角度θmax,进而可得L的最大值计算公式:
(8)
设F为阻尼器设计屈服力,在不考虑轴力和剪力的情况下,可结合公式(7)、(8)由材料屈服应力σy反推阻尼器最大截面宽度,得:
(9)
其中:
Δθmax=|a·tanα·cosθmax-b·sinθmax+
b·sinθS-a·tanα·cosθS|
根据等应力分布条件,在不考虑轴力和剪力的情况下,由公式(7)、(9)可得任意θ∈(θS,θE)截面对应的截面宽度Hθ计算公式:
(10)
其中:
Δθ=|a·tanα·cosθ-b·sinθ+b·sinθS-
a·tanα·cosθS|
通过式(9)和式(10),将各已知参数代入,即可得出基于等刚度原理的阻尼器截面宽度Hθ设计值,进而得出对应的阻尼器轮廓曲线。
2.3 一次刚度计算
根据能量法基本原理,弹性体在静荷载作用下发生变形时,荷载所做的功将以应变能的形式贮存于弹性体内部,在不考虑轴力和剪力的情况下,外力所做的功等于所产生的弯曲应变能。由此可得系统能量方程为:
(11)

结合公式(3)的截面弯矩计算公式,并将式(10)带入(11)进行化简,可得:
(12)
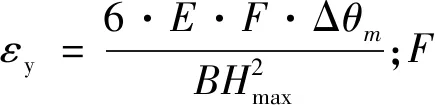
进而阻尼器的一次刚度可由下式得出:
(13)
3 有限元仿真分析
3.1 有限元模型
采用Ansys有限元仿真软件建立实体单元模型,选用solid185六面体单元,网格大小控制为5 mm,阻尼器两端采用销轴连接,轴与孔之间建立接触单元,约束和载荷施加于销轴上,具体详见图3。
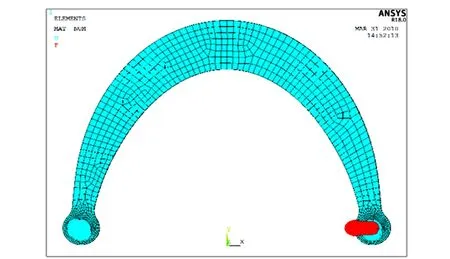
图3 阻尼器有限元模型
由于存在往复加载及反向塑性变形的情况,仿真计算中应考虑包辛格效应的影响,材料模型选择多线性随动强化模型[12]。阻尼器材料选用Q345钢,其本构关系由试验得出,并将名义应力应变关系转换为真实应力应变关系,具体详见图4。
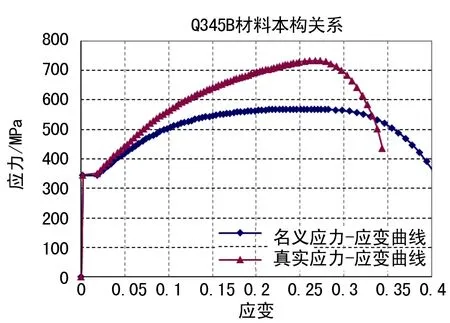
图4 Q345材料应力应变关系
模型的设计参数如表1所列,仿真工况分为力加载和位移加载两种,详见表2。工况一为设计屈服力加载,主要分析阻尼器弹性变形阶段的力学性能;工况二为大位移往复加载,主要分析阻尼器的弹塑性滞回效应及力学性能。

表1 阻尼器模型设计参数
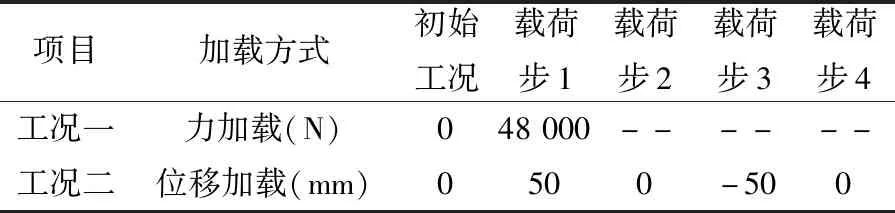
表2 加载工况
3.2 结果分析
3.2.1 工况一(力加载)
表3为一次刚度计算结果,其中变形量取自销轴沿x方向的位移,一次刚度由加载载荷及变形量计算得出。由表中数据可知,在弹性变形范围内,理论计算结果和有限元仿真结果比较接近,变形量和一次刚度的最大误差分别为-1.94%和2.45%,表明所提出的计算方法是比较准确的,计算结果有一定的可靠性。
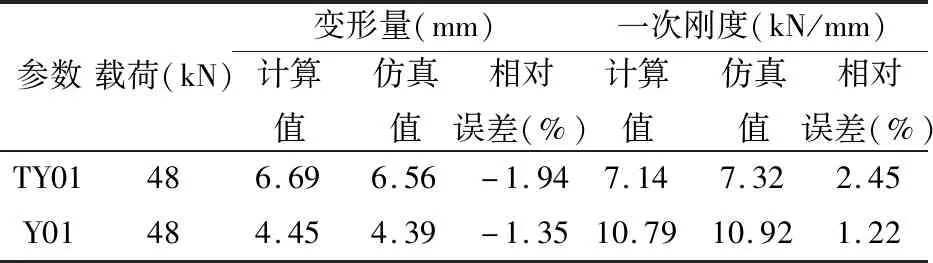
表3 刚度计算结果对比
图5为两种模型的等效应力分布图,应力最大值分别为375.43 MPa和360.00 MPa,比理论值345 MPa大了8.82%和4.35%,这是因为在理论计算中忽略了正应力和切应力的影响,计算结果在一定程度上要小于实际仿真值,该误差符合理论规律并且在可控范围之内,也再次验证了设计结果的可靠性。根据等效应力分布图可知,两种模型的应力沿径向均呈比较规律的层状分布,各截面能同时进入塑性变形状态,基本达到了等刚度的设计效果。

图5 工况一对应的等效应力分布图
3.2.2 工况二(往复位移加载)
现有的理论计算方法仅适用于弹性变形阶段,一旦阻尼器发生较大的塑性变形,公式便不再适用,对应的力学性能也无法有效预测,因此需要借助有限元仿真方法对阻尼器的弹塑性性能做进一步的分析和评价。图6为3.1节所述往复位移加载工况下TY01模型对应的塑性累积应变分布图。
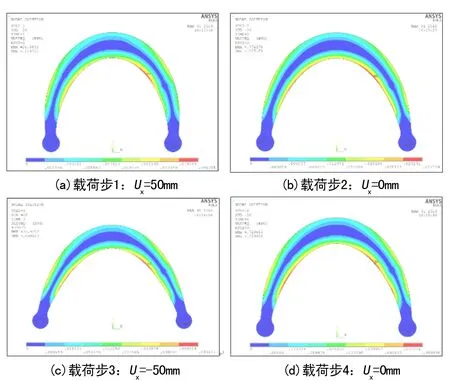
图6 工况二对应的塑性累积应变分布图
可见在大位移拉压循环加载过程中,参与塑性变形的面积较大,金属材料性能得到了有效发挥,表明该阻尼器具有较好的耗能效果。另外,在变形过程中阻尼器中心线附近的材料始终保持在弹性变形阶段(塑性应变为0),保证了连接的可靠性,避免了整体断裂现象的发生。
图7为仿真工况对应的滞回效应曲线,该曲线呈现出比较明显的双线性特征,经过近似处理[13]后可拟合出该阻尼器的双线性滞回曲线模型,对应的参数详见表4所列。

图7 阻尼器滞回效应曲线

表4 阻尼器特性仿真结果
(13)
式中:F为阻尼力大小;x为实际变形量。
根据仿真结果,阻尼器一次刚度与理论计算基本一致,二次刚度约为一次刚度的2%左右,因此在理论计算中一次刚度可直接由公式求出,二次刚度可按一次刚度的2%选取。
4 结 论
利用理论计算及仿真分析方法,可以有效的对椭圆弧形金属阻尼器的力学性能进行预测和分析,本文对该类型的阻尼器的设计进行了基础性的研究,得出了以下结论:
(1) 建立了椭圆弧形金属阻尼器的力学模型,并利用等刚度原理提出了椭圆弧形金属阻尼器的结构计算公式。
(2) 利用有限元仿真工具对设计公式进行了验证,表明该公式具有较高的准确性,基本达到了等刚性的设计目标,阻尼器设计刚度与仿真误差在2.5%以内。
(3) 椭圆弧形金属阻尼器具有明显的双线性滞回特性,可根据相关计算公式建立阻尼器的滞回曲线模型,为相关设计提供参考依据。
