基于分布式电源选址定容的配网降损方法研究

王 涛， 贺春光， 周兴华， 邵 华， 耿光飞， 檀晓林

（1.国网河北省电力有限公司经济技术研究院， 河北 石家庄 050000； 2.北京中恒博瑞数字电力科技有限公司， 北京 100085； 3.中国农业大学 信息电气工程学院， 北京 100083）

0 引言

近年来，分布式电源（DG）在配电网中的渗透率日趋提高，给配电网的供电可靠性、电能质量等造成一定的不利影响， 其影响的程度与DG 接入位置及接入容量密切相关[1]，[2]。 DG 的合理接入能够减少线路损耗，提高系统效率和可靠性，降低系统总成本[3]，[4]。 因此，设计经济合理的DG 选址定容方法，对DG 接入位置和容量进行优化，同时提高分布式电源和配电网运行的安全性、 可靠性和经济性，已成为当前研究的热点[5]，[6]。

文献[7]使用蚁群算法（ACA）和和声搜索（HS）来解决含DG 接入的网络重构问题。 文献[8]引入猫群优化算法以优化DG 接入单元的位置和容量。 文献[9]引入混合整数非线性规划（MINLP）以实现多目标优化， 通过选择DG 的最优容量和位置，在降损的同时提高了供电可靠性。 文献[10]通过遗传算法， 在考虑系统约束的情况下确定DG的最优位置及容量， 最大化系统负载裕度以及优化电压曲线。 文献[11]采用遗传算法和模糊算法将原始目标和约束条件转化为模糊加权的单目标函数，以优化遗传算法。 文献[12]使用基于蒙特卡洛模拟嵌入式遗传算法， 以最大程度地降低网损为目标， 通过优化DG 的选址和规模降低容量成本。 文献[9]，[13]在分布式电源接入优化问题的研究中，将经济性因素纳入考量范围，但没有考虑节点平均电压偏移等电能质量方面的因素。目前，对于分布式电源选址定容方案的研究中较少同时考虑经济性和电压分布， 少数研究建立的多目标优化模型存在多目标处理简单、 加权系数选取与实际情况相差较大的问题。

本文将大规模辐射型配电网中DG 的位置选取和容量确定作为求解变量， 以降低配电网运行线损为优化目标， 同时考虑实现配电网整体较好的电压分布，采用CPSO-NSGA 进行模型求解。同时，针对配电网节点规模较大的实际，通过线损敏感度系数法筛选出适宜DG 接入的母线集合，为配电网降损的DG 选址方案制定的科学性提供了参考。

1 线损敏感系数

针对配电网节点规模较大的实际， 本文通过线损敏感度系数法（Loss Sensitivity Factors， LSF）筛选出适宜DG 接入的母线集合， 大大减少了搜索范围。 图1 为辐射型配电系统等效电路图。

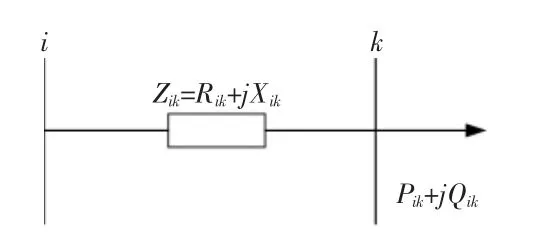
图1 辐射型配电系统等效电路图Fig.1 Radial distribution system equivalent circuit

考虑到配电网DG 的选址定容对网络拓扑节点的有功、无功功率均会产生影响，本文将线损敏感度因子定义如下：

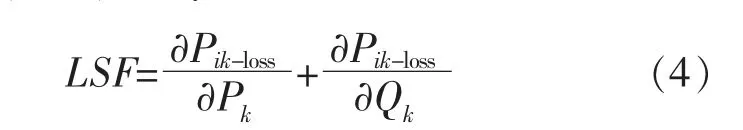
LSF 是根据典型负荷工况下的潮流计算得出的，对于给定系统的所有线路，其值按降序排列。定义支路位置向量为“bpos[i]”，用于存储按值的降序排列的各支路的末端节点，“bpos[i]”向量元素的降序将决定考虑支路补偿的顺序。 该序列仅受LSF 数值大小的影响，因此，在DG 实现降损目标的选址定容中作用明显。 在“bpos[i]”向量支路里，将电压标幺值通过norm[i]=V[i]/0.95 进行归一化。 对于归一化后的电压标幺值小于1.01 的支路，将其视为DG 可以接入的候选支路， 形成候选支路集合。 LSF 决定了线路补偿DG 的顺序，而电压标幺值的归一化值则决定了支路是否需要DG 补偿。如果配电网拓扑某条支路上的电压正常（即norm[i]>1.01），则该总线无需补偿，并且该支路也不会列在候选支路集合中。 以IEEE16 节点配电网为例，表1 给出了有功功率线路LSF 的降序排列以及15 条支路电压标幺值的归一化值。

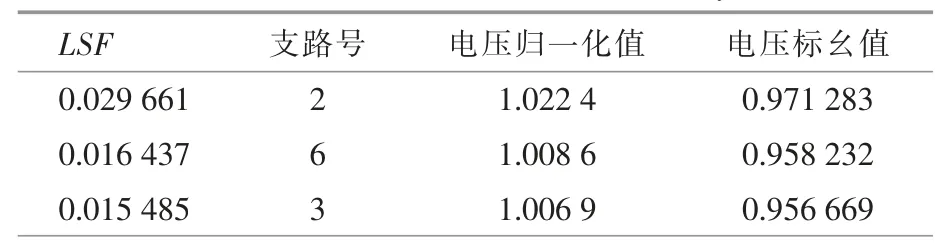
表1 线损敏感度因子的降序排列Table1 Loss sensitivity coefficient’s placed in descending order of a 15-bus radial distribution system

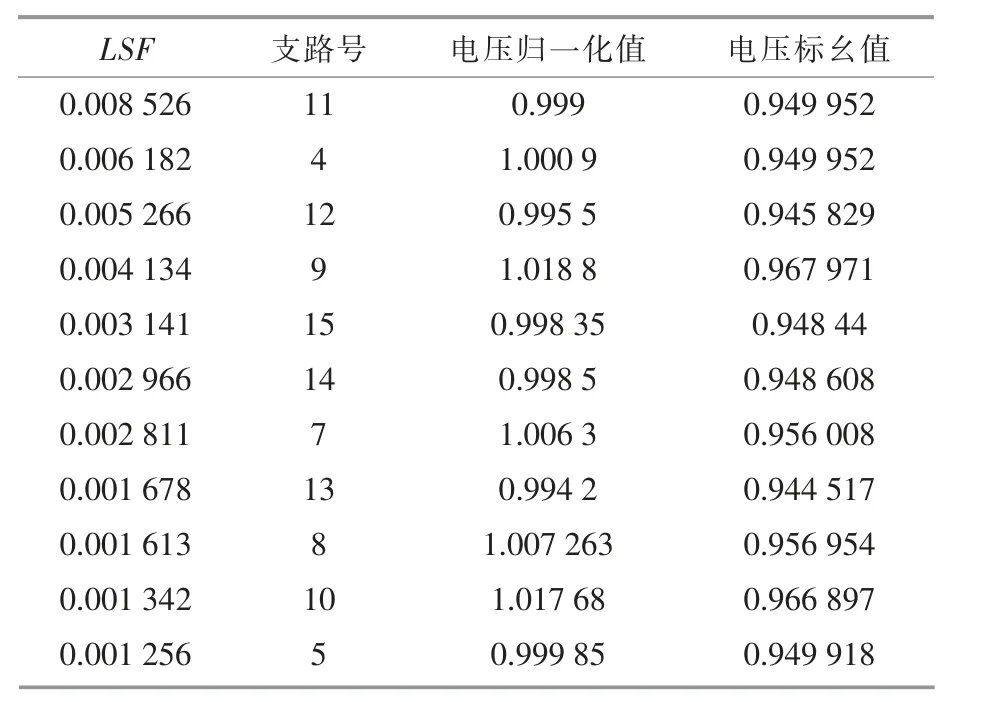
续表1

2 基于DG 选址定容的配网降损模型

2.1 目标函数

本文提出的基于DG 选址定容的配网降损模型，在考虑降低线路功率损耗的同时，改善电压分布和电压稳定指数，在满足各约束条件的前提下，最大化配电网和分布式电源效益， 使得配电网经济性最优、节点电压偏差最小。

优化模型的目标函数为

式中：子目标函数f1为线损目标函数；子目标函数f2为电压分布目标函数；子目标函数f3为静态电压稳定裕度。

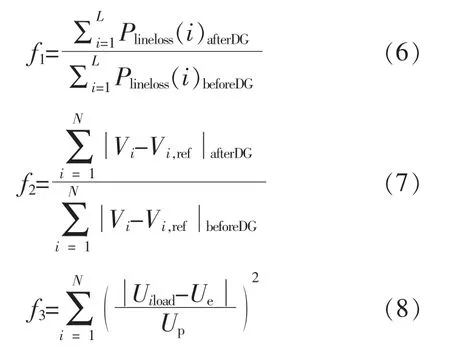
式中：Plineloss（i）beforeDG，Plineloss（i）afterDG分别为DG 接入前、 后的有功网损；Vi为节点i 的电压；Vi，ref为节点i 的参考电压， 一般为标幺值1；Uiload为负荷节点i 的电压标幺值；Ue为负荷节点额定电压，取值为1；Up为节点电压允许偏差，取值为5%。

2.2 约束条件

①潮流等式约束

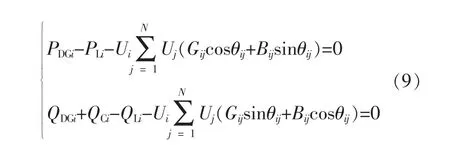
式中：N 为配电网总节点数；Gij，Bij分别为节点i和j 间的馈线电导、 电纳；PDGi，QDGi分别为节点i分布式电源注入的有功、无功功率；PLi，QLi分别为节点i 负荷的有功、无功功率；QCi为节点i 处无功补偿容量。

②节点电压约束

④线路容量约束

为了防止功率倒流，电网的装机容量被限制为

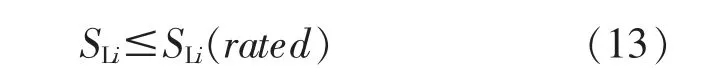
式中：SLi，SLi（rated）分别为节点i 的装机容量、限定装机容量。

3 配网降损模型的求解

粒子群优化（PSO）算法在求解大规模优化问题上具有很快的收敛速度和全局寻优能力[14]，但在求解多目标优化问题时， 权重系数的选择一般依据经验主观决定，可能与实际情况偏差较大。非支配排序遗传算法（NSGA）适用于求解多目标优化问题，但算法计算复杂度较高，用时较长。 本文提出采用CPSO-NSGA 求解分布式电源选址定容的多目标优化问题，具体实施步骤如下：

①初始化， 包括在约束条件范围内随机产生粒子群的初始位置及速度、粒子种群大小、设定最大迭代次数以及目标函数个数等；

②根据粒子初始位置， 即初始各负荷节点的分布式电源接入容量， 调用潮流程序计算网络损耗，再调用蒙特卡洛模拟程序计算可靠性指标；

③基于小生境技术对初始种群进行多目标全局寻优；

④对粒子速度函数进行更新， 再更新粒子位置，判断粒子的速度和位置变量是否越限，对其进行约束；

⑤求得更新后各粒子的子目标函数值， 形成混合种群，进行非支配排序，选择下一代种群；

⑥计算得到当前全局最优解gbest，检查是否达到最大迭代次数，如果达到，转步骤⑦，否则转步骤③；

⑦输出最优解，程序结束。

CPSO-NSGA 流程图如图2 所示。

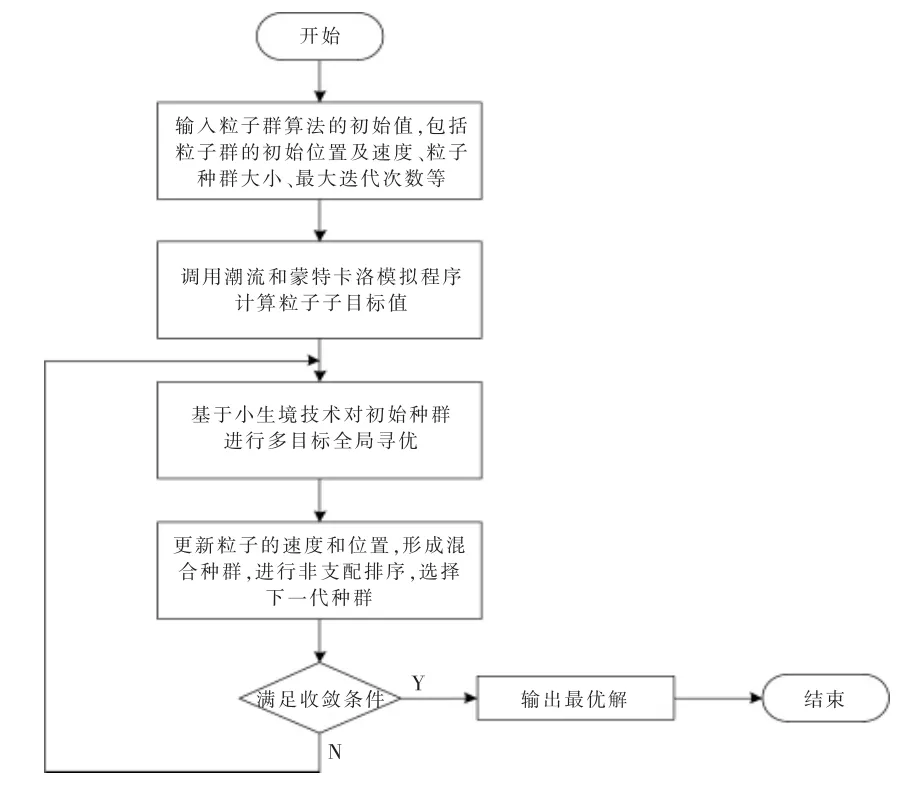
图2 CPSO-NSGA 流程图Fig.2 Flow chart of the CPSO-NSGA

其中， 基于小生境技术的多目标全局寻优过程如下：首先初始化各方案适应度值，将其设置为0；然后生成区间为[1，2]的随机数k，针对每一个优化目标，对方案进行排序；计某方案排序为i，若i=1，即为该子目标下的最优方案，则适应度值累加k×pop（pop 为方案数），否则累加（pop-i）2。最优解为各子目标适应度累计值最小的方案。

4 仿真分析

4.1 仿真模型设置

本文采用IEEE33 节点标准测试系统， 设定单节点安装DG 容量不高于500 kV·A。 网络拓扑如图3 所示，各支路数据及负荷情况如表2 所示。

图3 IEEE33 节点配电系统接线图Fig.3 Wiring diagram of the IEEE33 nodes distribution system

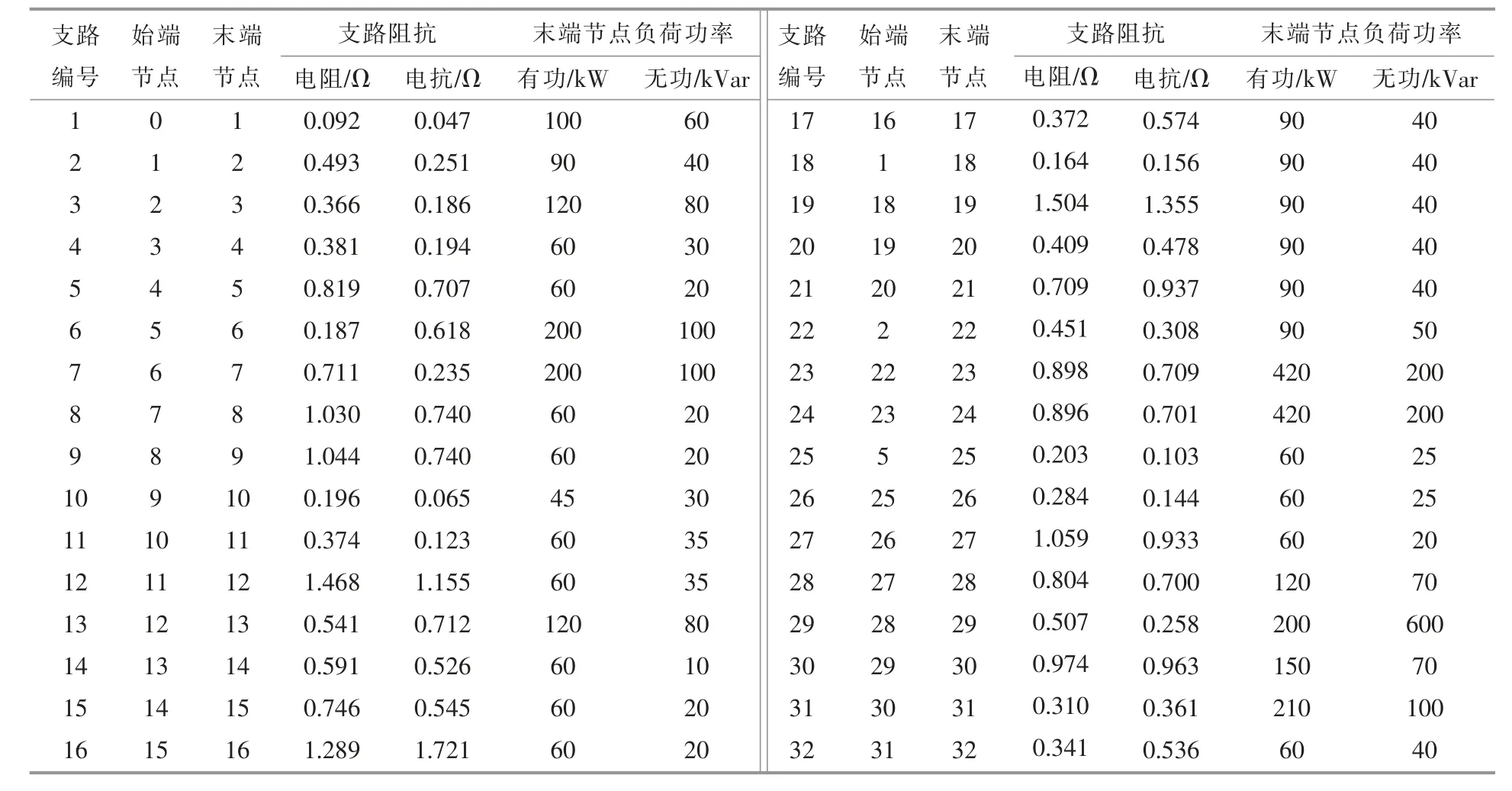
表2 IEEE33 节点配电网数据Table 2 Parameter values of the IEEE33 nodes distribution network

本文采用CPSO-NSGA 求解基于DG 选址定容的配电网降损模型。初始参数设置：初始种群大小为90，即每代种群中含有90 个粒子；最大迭代次数为200；子目标函数个数最大值为3，即最多可同时优化3 个子目标；控制变量为2 个，即允许接入分布式电源的数量为2， 且各节点分布式电源接入容量为0～500 kV·A，功率因数均取0.9。

此外， 考虑到对所有节点进行选址情况过于复杂， 针对IEEE33 节点本文通过线损敏感度系数法进行筛选， 其中5 号节点和2 号节点敏感度系数最高，分别为0.046 6 和0.029 6，然而其电压标幺值的归一化值分别为1.019 1 和1.049 5，不符合接入要求。 最终筛选后的两个适宜接入节点分别为8 号和12 号节点。分布对比图，其中，方案一为DG 采用线损敏感度

4.2 仿真算例

仿真算例采用随机选取法和线损敏感度系数法，分别选取11，31 号和8，12 号节点作为节点备选集合。

图4 为200 次迭代后的最优种群中， 采用线损敏感度系数法选取节点的配电网线损目标函数；图5 为电压分布目标函数变化；图6 为静态电压稳定裕度； 图7 为两种接入节点方案下的电压系数法，方案二为DG 采用随机选取法。

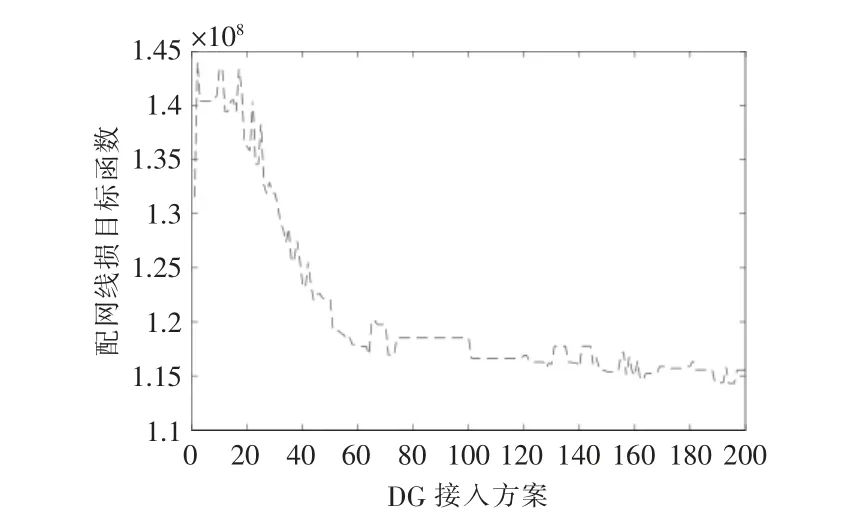
图4 配电网线损变化图Fig.4 The diagram of network loss

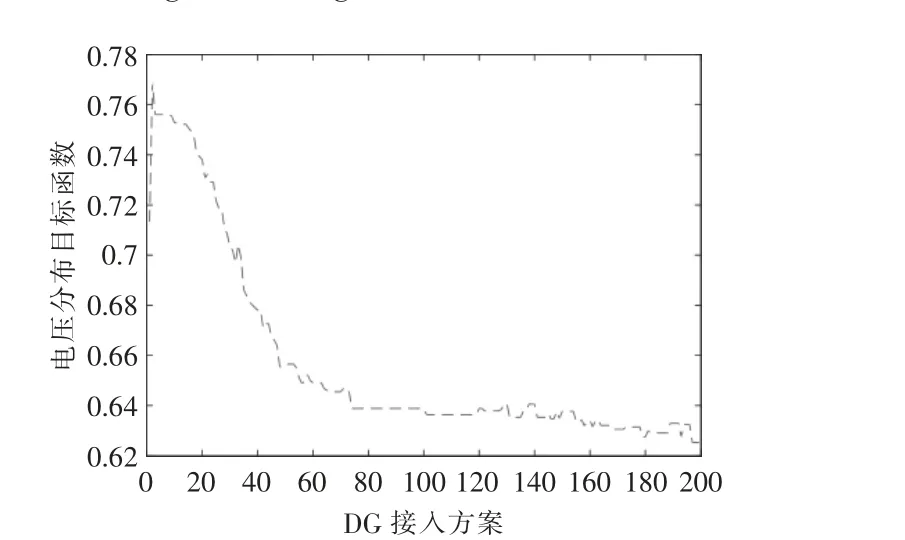
图5 电压分布目标函数Fig.5 The diagram of voltage distribution objective function

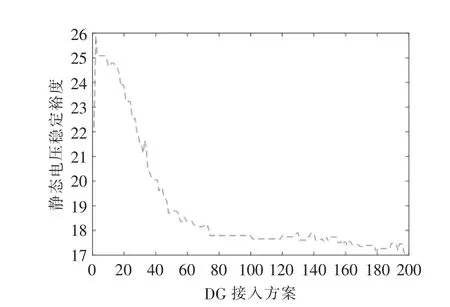
图6 静态电压稳定裕度Fig.6 The diagram of static voltage stability margin

由图4～7 可以看出， 就某一DG 接入方案而言，无法使得各子目标均达到最优。 例如，当选取网损最小方案194 时， 线损目标函数值为1.06e+08，进行单位换算可得网损为53.6 kW，然而此时电压分布目标函数值为0.62， 静态电压稳定裕度为15.19，可以看到，静态电压稳定裕度指标偏大，采用该方案易出现电压越限的情况。

由图7 可以看出，在降低网损的基础上，方案一相较于方案二实现了更好的电压分布， 且方案二的线损目标函数值为1.15e+08， 降损效果也不如方案一。

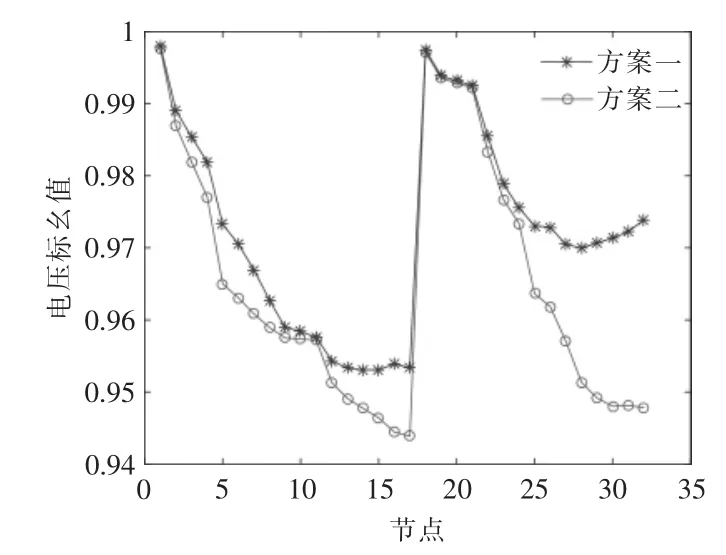
图7 配电网节点电压图Fig7 Distribution network node voltage figure

表3 给出了选址定容最终的优化方案， 即节点8 接入分布式电源为416.56 kV·A，节点12 接入分布式电源为485.43 kV·A。 该最优方案是基于小生境技术在最优种群中选出一个适应度较大的个体作为最优解， 可保证各子目标函数非劣程度最好。 表4 为采用表3 方案时的各子目标函数值及算法性能。由表4 可以看出，该方案各子目标函数值均较好， 没有在某个子目标维度上出现极端劣解，在可靠性和经济性方面达到了综合最优。整个求解过程耗时97.12 s。

表3 最优选址定容方案Table 3 Optimization sitting and sizing scheme of DGs

表4 优化结果及算法性能Table 4 Optimization results and algorithm performance

5 结论

本文提出的基于分布式电源选址定容的配网降损方法， 综合考虑了配电网运行经济性和电压良好分布两方面因素。 针对配电网节点规模较大的实际， 采用线损敏感度系数法对DG 接入的母线集合进行预筛选， 减少了选址工作量。 采用CPSO-NSGA 进行优化模型求解， 将其应用到IEEE33 节点系统中。 结果表明，通过采用小生境技术在最优种群中选出相对最优解， 使得DG 选址定容方案在经济性和电压分布两个维度上达到了综合最优。