偏差考核下售电公司的电动汽车电价策略研究

黄春辉， 朱自伟， 裘昕月， 黄 彪， 吴 昊， 钟少云， 帅挽澜

（南昌大学， 江西 南昌 330031）

0 引言

随着我国经济的快速发展，电力工业的老旧体制已经无法完全满足市场的需求。 为了更好地促进电力工业的竞争、 提高电力资源的利用率、构建安全稳定的用电环境，2015 年，我国颁布了《关于进一步深化电力体制改革的若干意见》，新一轮的电力体制改革由此拉开了序幕。 目前，各省市均出台了相关的电力市场交易规则来促进电力市场改革。 虽然各省市的电力市场交易规则不尽相同，但是均包含了电量偏差考核机制。 为了保证电力产供销的动态实时平衡，售电公司申报电量与实际售卖电量应一致，超出偏差允许范围的售卖电量或未售卖电量要缴纳较高的罚金。在电力市场改革的初期，各省市均给予了占申报电量2%～5%的免考核电量， 但是随着改革的深入，免考核电量将越来越少。 由于电力负荷具有复杂性、分散性和随机性等特点，现阶段电力负荷的预测难度较大。 售电公司在电力市场交易时，须要找出降低偏差电量的方法以减少偏差考核费用，否则其收益将会大大降低，甚至出现亏损。

目前，许多专业人员研究了售电公司电量偏差问题的解决办法。 文献[1]提出通过制定适当的合同奖惩条款规范交易相关方的调整行为，并对偏差电量进行责任认定和责任处罚，由此减少偏差电量而优化电网的调度。 文献[2]将备用成本进行责任分摊作为解决电量偏差的方法。 由于电力系统为弥补偏差电量而设置、 启用的备用服务增加了供电成本， 因此备用成本应该由引起偏差电量的各责任方分摊支付。 文献[3]提出了售电公司可以通过调控中断负荷来规避风险、提高收益、实现企业与用户双赢的方法， 但该方法不具备解决负偏差电量的能力。 文献[4]提出通过售电公司之间签订电量互保合同来保证双方免于偏差考核，然而， 目前只有极少数省市允许售电公司之间签订此类合同， 未来是否会有更多的省市开放电量互保机制还不得而知。文献[5]从电力用户的视角，研究了电力改革模式对用户购电成本的影响和不同偏差程度下用户的盈利点。

随着电动汽车（Electric Vehicle，EV）产业的迅猛发展及国家的大力支持， 规模化的EV 车载电池将成为智能电网中重要的储能元件。EV 车载电池具有良好的可调节性， 可以作为降低售电公司偏差电量的有效手段。 只要通过一定的控制策略引导EV 用户的充放电行为， 使其在某些时段多充电，在另外时段向电网放电，便可调节售电公司偏差电量。 在售电公司与EV 互动的过程中，双方的利益具有一定程度的对抗性与合作性， 并非单纯的此消彼长，也并非绝对的合作共赢。 例如，售电公司预计出现正偏差时，EV 放电抵消了售电公司的预计偏差电量，使售电公司免于偏差考核且保证其正常收益， 同时售电公司向EV 用户支付一定的费用进行补偿。 但是EV 的放电行为却牺牲了部分行驶需求，且增加了电池损耗。 目前，关于售电公司与EV 互动来减少偏差电量的研究较少，而与之类似的电网与EV 互动的研究较多。本文研究的重点是寻求成本与收益之间的平衡，保证双方在互动的过程中均可获得一定的收益。本文将参照车网互动中EV 为电网提供削峰填谷服务的互动原理， 构建通过EV 的充放电行为来弥补售电公司偏差电量的互动机制。

博弈论是一种先进的优化工具，主要用于研究多个利益相关的主体进行优化决策。售电公司与EV 互动的问题是一个博弈的问题，通过博弈论的相关理论寻求保证双方互动获利的均衡点，便可以很好地促进售电公司与EV 的互动。 在众多博弈论中，演化博弈论不再将博弈方视作超级理性的，而是认为博弈方是有限理性的，且通过试错的方法达到博弈均衡。 这十分符合EV 用户群体多样性的特点。 EV 用户群体通过尝试不同的策略，并比较各策略的收益达到博弈均衡。 因此， 本文从演化博弈论的角度对售电公司与EV之间的利益关系进行分析，以促进互动、保证双方获利，为演化稳定目标对博弈中的相关因素进行研究，为售电公司与EV 互动解决偏差电量问题提供指导。

1 售电公司电量偏差考核机制

目前，各地区的偏差电量考核规则不尽相同。例如： 以取消一定时间段参与直接交易市场资格或终止合同的方式进行惩罚； 暂时通过滚动调整方式处理偏差电量；以收取考核费用实行惩罚[3]。本文仅讨论收取考核费用的惩罚方式， 对于其他考核方式不做详细研究。 图1 为根据某省电力市场交易规则而绘制的偏差电量考核流程图。

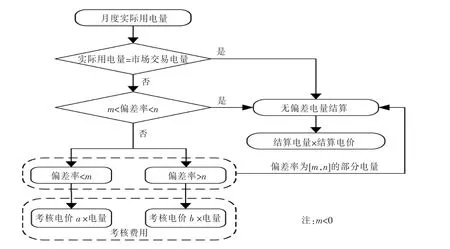
图1 偏差电量考核流程Fig.1 Energy deviation penalties process

为了便于研究分析，本文做出如下假设。

①长协分月电量和月度集中竞价电量统称为市场交易电量，均采取月结月清的结算方式；

②偏差考核费用由售电公司全包， 售电公司不对电力用户进行考核；

③售电公司与电力用户合同约定将收益的α倍返还给电力用户。

偏差率的定义：

式中：Qa为月度实际用电量；Qv为市场交易量。

若β＜0，表示售电公司出现负偏差；若β＞0，表示售电公司出现正偏差。

（1）无偏差电量或偏差率在[m，n]之内的结算

当电力用户的实际用电量等于售电公司的市场交易量，或者售电公司的偏差率在[m，n]之内时，无须对售电公司进行考核。

（2）有偏差电量，且偏差率大于n 的结算

当售电公司出现了较大的正偏差时， 结算方法为

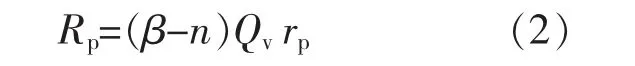
式中：rp为正偏差考核电价。

（3）有偏差电量，且偏差率小于m 的结算

当售电公司的偏差率小于m， 即出现较大负偏差时，售电公司要支付一定量偏差考核费用，结算方法为

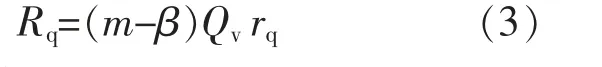
式中：rq为负偏差考核电价。

2 演化博弈论简介

演化博弈理论来自于达尔文的生物进化论。在生物进化的过程中，物竞天择，适者生存。 只有适应当时环境获得较高“收益”的物种才能够生存下来，而不适应环境获得较低“收益”的物种只能在竞争中被淘汰。

演化博弈论亦是如此。 假设存在一个个体数为n 的足够大群体，该群体中的每一个个体都有相同的策略集合s={s1，s2，…，sk}，用f（si，s）表示选择策略si的个体与其他选择策略s1，s2，…，sk的个体博弈后获得的收益。 假设某个体选择突变策略s′∉s， 而其竞争对手均选择策略集合s 中的策略；若选择突变策略的平均收益大于其他策略的平均收益，则该群体中的个体会趋向于选择该突变策略。演化博弈论假设个体选择突变策略的调整速度与其收益超过平均收益的幅度成正比，则有如式（4）的复制动态方程，求解该方程得到的稳定状态被称为演化稳定策略（ESS）。

式中：xs′为该群体中每个个体选择策略s′的概率；f（s′，s）为该群体中选择策略s′的期望收益；f（s，s）为群体的平均期望收益。

演化稳定状态具有较好的抗干扰性， 即使受到一定的干扰，系统也能够恢复至稳定状态。

3 互动博弈模型的建立

图2 为售电公司与EV 的互动示意图。

图2 售电公司与EV 互动示意图Fig.2 Interaction diagram of electricity retailers and EV

如图2 所示， 在售电公司与EV 互动的模型中，双方均有合作与不合作两种策略可选择。 就售电公司而言：合作策略就是指售电公司通过向EV 用户给予一定的补偿来引导EV 的充放电行为，弥补自身的偏差电量，保证自身免于偏差考核而减少收益损失；不合作策略是指售电公司不引导EV 进行充放电，且接受偏差考核。 就EV 用户而言： 合作策略是指EV 用户接受售电公司的补偿引导机制， 按售电公司的需求进行充放电；不合作策略是指EV 用户不参与互动， 按正常的习惯进行充电。 为了便于计算，本文假设双方合作的情况下，售电公司无偏差电量。

使用演化博弈来分析售电公司与EV 互动的电价策略。 假设售电公司参与互动即合作的概率为x，则其不合作的概率为1-x；EV 用户合作的概率为y，则其不合作的概率为1-y。 x，y 均为关于时间t 的函数。 引入离散决策变量p 和q，当售电公司出现正偏差时，p 为1，q 为0，出现负偏差时，p 为0，q 为1。

互动博弈模型的主要参数：Rprc1为售电公司无偏差电量情况下的收益；Rprc2售电公司受到偏差考核情况下的收益；Qd为正偏差电量；Qc为负偏差电量；rd为EV 的放电电价；Co为售电公司合作的单位运营成本；Bprc为售电公司选择合作而EV 选择不合作时给售电公司带来的损失；Rv为EV 用户正常行驶所带来的收益；Kb为EV 用户在充放电过程中的单位电池损耗；r 为居民用电电价， 即EV 不参与合作时的充电电价；rc为EV 的充电电价；ΔQc为售电公司有负偏差时，EV 较日常所多出的充电电量；Bv为EV 用户选择合作而售电公司选择不合作时给EV 用户带来的损失。

售电公司选择合作策略的期望收益为

式中：Rprc1－Co（pQd+qQc）为售电公司与EV 用户均选择合作策略时，售电公司获得的收益，该收益是售电公司无偏差电量情况下的收益减去运营成本；（Rprc2-Bprc）为售电公司选择合作策略而EV 用户选择不合作策略时售电公司获得的收益， 该收益是售电公司受到偏差考核情况下的收益减去EV 选择不合作时给售电公司带来的损失。

式中：[Rv+ pQd（rd-r-Kb）+ qQc（r－rc）－qΔQcKb]为售电公司与EV 用户均选择合作策略时，EV 用户群体获得的收益， 该部分收益的第二项为售电公司出现正偏差时，EV 放电获得的收益及电池损耗成本，第三项为售电公司出现负偏差时，EV 充电获得的收益，第四项为EV 充电的电池损耗成本；（Rv-Bv） 为EV 用户选择合作策略而售电公司选择不合作策略时，EV 用户群体获得的收益。

4 模型分析

根据以上分析， 建立演化博弈模型的收益矩阵，见表1。

表1 演化博弈收益矩阵Table 1 Evolutionary game income matrix

令F（x）=0，F（y）=0，可在平面s={（x，y）；0≤x，y≤1} 中得到5 个均衡点， 分别为E1（0，0），E2（0，1），E3（1，0），E4（1，1）和E5（x5，y5），如图3 所示。

图3 售电公司与EV 互动动态演化相图Fig.3 Dynamic evolution phase diagram of sales company and EV interaction

根据李雅普诺夫稳定性理论可得：E1（0，0）和E4（1，1）为稳定均衡点；E2（0，1）和E3（1，0）为不稳定均衡点；E5（x5，y5）为鞍点。 所以，双方均选择合作策略与双方均选择不合作策略为该博弈的演化稳定策略。

由图3 可知， 当售电公司与EV 用户的初始状态落在四边形E2E5E3E1内的任意一点时，系统最终会收敛于E1（0，0），即双方都选择不合作策略。此时售电公司不得不接受偏差考核，支付大量的偏差考核费用， 而且EV 用户也不能从售电公司获得补偿收益。 当售电公司与EV 用户的初始状态落在四边形E2E5E3E4内的任意一点时，系统最终会收敛于E4（1，1），即双方都选择合作策略。 此时售电公司只须向EV 用户支付一定的补偿，即可免于偏差考核，减少损失；EV 用户也可以通过与售电公司互动获取一定的补偿。

同时可见，鞍点E5（x5，y5）越靠近稳定均衡点E1（0，0），四边形E2E5E3E4的面积越大，系统向稳定点E4（1，1）演化的概率就越大，而向E1（0，0）演化的概率就越小。

四边形E2E5E3E4的面积为

对式（14）中的Qd，rd，r，Qc，Kc，ΔQc，Rprc2分 别求偏导，得到的结果均大于0。 由此可知，四边形E2E5E3E4的面积随上述7 个参数的增大而逐渐增大，系统向稳定点E4（1，1）演化的概率就越大。

同理，对式（14）中的Kb，rc，Bv，Bprc，Rprc1分别求偏导， 得到的结果均小于0。 可知四边形E2E5E3E4的面积随上述5 个参数的增大而逐渐减小，系统向稳定点E1（0，0）演化的概率将会变大。

在稳定点E4（1，1），即双方都选择合作策略的情况下，为了保证双方均可获利，形成稳定的合作互动关系，须满足以下关系式：

式中：Δr 为统一出清价差；α 为售电公司与用户协议约定将收益的α 倍返还给用户，α∈（0，1）。

式（15）为从售电公司获利的角度看，各参数应满足的条件。 式（16）为从EV 用户获利的角度看，各参数应满足的条件。充放电电价作为售电公司引导EV 用户充放电行为的主要手段， 是本文的主要研究对象。

满足上式的rc即为保证售电公司与EV 用户在互动中均获利的充电电价。

将不等式（15），（16）修改成等式并联立，解得的β 为售电公司与EV 互动时可以保证双方都获利应满足的最小偏差率βmin。 换言之，当售电公司预计出现偏差率大于βmin时，售电公司寻求与EV互动才可能找到保证双方均可获利的充电电价。

当售电公司出现正偏差，即p=1，q=0 时

5 算例分析

5.1 算例参数及场景假设

以某售电公司为例， 假设该公司可以根据某月前15 d 的用电负荷数据对后15 d 的用电负荷进行预测， 此时的预测数据较其在电力市场申报电量时的预测数据更加准确。 公司便可以得出该月可能会出现的正负偏差电量， 并计算出预计偏差率。 以此为依据，在该月的后15 d 引导EV 充放电，弥补预计的偏差电量。

假设公司市场交易量为4 000 万kW。该售电公司所在省份的偏差允许范围为±3%，即m 取值为-0.03，n 取值为0.03。 正偏差考核电价rp为0.01 元/（kW·h），负偏差考核电价rq取为0.02 元/（kW·h），月度出清价差为-0.384 元/（kW·h）。 假设售电公司与电力用户协议约定将收益的0.5 倍返还给电力用户，即α 取0.5。 由于目前尚无售电公司与EV 互动的相关研究， 所以售电公司互动的单位运营成本Co可根据车网互动中电网的运营成本来选取，Co=0.035 元/（kW·h）[6]。 文献[7]提出了电池损耗最快和最慢两种极端情况下的电池损耗，分别为87.5 美元/（MW·h）和20.1 美元/（MW·h），本文取其平均值53.8 美元/（MW·h），即0.34 元/（kW·h） 为EV 用户在充放电过程中的单位电池损耗。 EV 用户不参与时的充电电价与充电桩的用电来源有关，如使用私人充电桩可按居民用电电价充电，约为0.6 元/（kW·h），使用公共充电桩则须按充电桩所属公司制定的电价进行充电，约为1.1～1.8 元/（kW·h）。为了保证EV 用户在互动中可以获得更低的充电电价，本文以某省夏季居民用电电价的第二档为例， 取r=0.73 元/（kW·h）。 售电公司出现负偏差，比EV 不参与互动时多出的充电电量ΔQc较难预计， 其值大致与售电公司的负偏差电量正相关； 负偏差越大，EV多出的充电电量也就越大。 假设ΔQc为Qc的s倍，即ΔQc=sQc且s∈（0，1），本算例取s=1/5。售电公司选择合作而EV 选择不合作， 给售电公司带来的损失Bprc和EV 用户选择合作而售电公司选择不合作，给EV 用户带来的损失Bv较难用具体的经济参数假设，故不做详细讨论。

5.2 充放电电价取值范围

根据上述假设分析，可以求得保证双方获利的充放电电价范围：

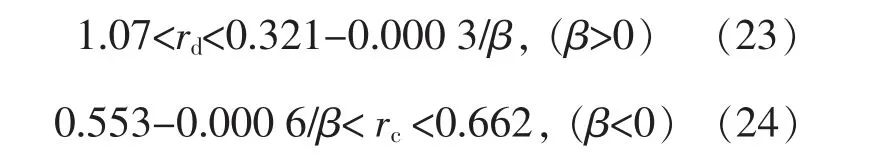
从EV 充放电的角度看， 由于电池容量有限且须要满足正常行驶，EV 弥补售电公司偏差电量也有一定的限度。

EV 参与放电互动时，假设每天放电一次，每次平均放电量为电池容量的1/3。 EV 参与充电互动时，假设每天充电一次，每次平均充电量为电池容量的2/3。故EV 能够弥补的最大正偏差率和最大负偏差率为

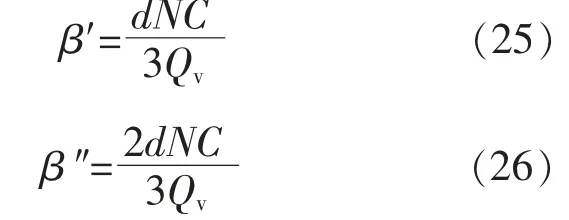
式中：d 为参与互动的天数；N 为参与互动的EV数量；C 为EV 电池的平均容量。

假设售电公司可以引导8 千辆EV 参与互动， 每台EV 参与每月后15 d 的充电或放电互动，且所有EV 电池的平均容量为50 kW·h，则β′=0.05，β″=-0.1。

图4 所示为放电电价取值范围。用户可获利的充电电价取值范围； 实线上方的区域表示售电公司可获利的充电电价取值范围。 实线上方与虚线下方重叠的区域即为保证双方互动均可获利的充电电价取值范围。 点划线m 右侧区域为偏差率大于-0.03 时的情况，此时售电公司并不会受到偏差考核。 虚线β″右侧区域为EV 能够弥补的偏差范围， 当偏差率小于-0.1 时，EV 并不能完全弥补售电公司的偏差电量。

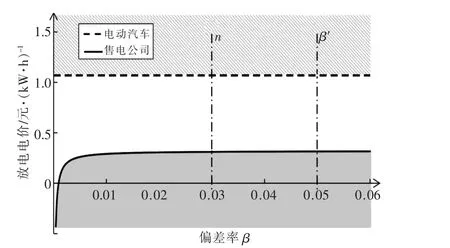
图4 放电电价取值范围Fig.4 Range of discharging price

若售电公司面临负偏差考核风险，即β＜-0.03 时，售电公司与EV 互动弥补负偏差可以使双方均获利。随着负偏差率的减小，售电公司的考核费用越来越高，EV 充电弥补偏差电量带来的收益也就越大， 所以其给出的充电电价底线就越低，如图5 中实线所示。 综上所述，保证售电公司与EV 用户双方均可获利的区域为ABCD。

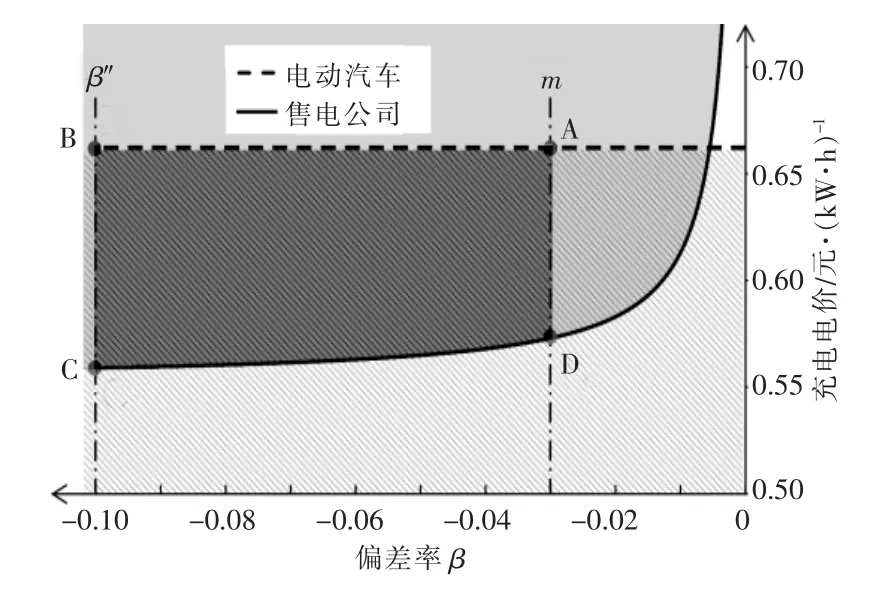
图5 充电电价取值范围Fig.5 Range of charge price

5.3 最小可行偏差率

式（21），（22）显示，随着考核电价rp和rq的变化， 售电公司寻求与EV 合作应该满足的最小偏差率也会随之改变。通过对图4 的分析可知，在现行条件下，售电公司出现正偏差时，向EV 寻求互动是不可能保证双方都获利的。因此，以下只分析售电公司出现负偏差时， 满足合作获利的最小偏差率。

根据考核电价rp和rq均由月度出清价差Δr 决定的假设，分析某省的月度出清价差变化规 律， 其 出 清 价 差Δr 值 为-0.446～-0.207 元/（kW·h）。 最小可行偏差率βqmin随月度出清价差Δr 变化而变化的曲线如图6 所示。

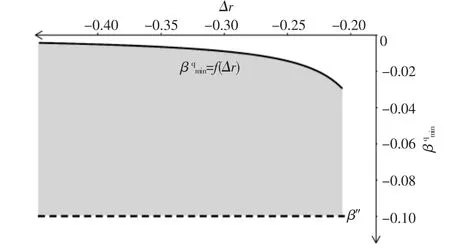
图6 最小偏差率随月度出清价差变化图Fig.6 Minimum deviation rate under different monthly clearing price

从图6 中可以看出， 随着月度出清价差的减小，保证双方获利的最小偏差率也随之减小。图中阴影区域表示售电公司与EV 合作能够找到保证双方获利的充电电价的负偏差率可行区域。 根据上节算例可以得知，EV 弥补偏差电量也是有一定的范围的， 因此图6 中的虚线是EV 能够弥补的最大偏差率。

6 结论

本文运用演化博弈论模拟了售电公司与EV用户互动的过程， 研究了影响演化过程的相关因素。为了促进双方的良性互动，通过算例分析了保证双方均可获利的充放电电价范围。

①当售电公司预计出现正偏差时，EV 用户参与互动，弥补偏差电量是无利可图的。 此时，售电公司支付的考核费用较小、购电成本过高，售电公司并不能从互动中获利。

②当售电公司预计出现负偏差时， 该负偏差率只要在保证双方获利的充电电价负偏差率的区域， 售电公司便可以根据电力市场的交易规则制定合理的充电电价，EV 用户参与互动弥补偏差电量可以使得双方均获得收益。 因为此时售电公司支付的考核费用较高，EV 弥补偏差电量的价值就越大， 而且售电公司也能从EV 充电中获得一定的收益。对于EV 用户来说，获得了更低的充电电价， 多出的充电电量也增加了EV 的使用时间。总之，制定合理的充电电价可以使得双方均从互动中获利。

③售电公司与EV 用户演化博弈的结果取决于各自的收益关系。 只有当双方均可以从合作互动中获利， 且双方合作概率的初始值符合一定的要求时， 演化博弈的结果才会使双方均选择合作策略。 为了促进合作， 除了要提高互动的收益之外，还要做好前期宣传工作，保证EV 用户合作概率的初始值在一个较高的水平。