适用于集群风电场送出线的选相元件研究

马 健， 樊艳芳， 李 锋， 张鑫宇

（1.新疆大学 电气工程学院， 新疆 乌鲁木齐 830046； 2.国网安徽省电力有限公司宿州供电公司， 安徽 宿州234000）

0 引言

大规模风电接入电力系统后，对传统继电保护装置的正常工作造成重大影响[1]～[5]。风电的接入在很大程度上改变了区域电网的电磁暂态特性，使得基于传统电力系统故障特征的继电保护无法正常动作[6]～[8]。 因此，有必要针对风电接入系统的继电保护进行充分研究。

风电场接入电网与常规系统的故障特征不同。 文献[9]～[11]分别从数学模型和运行控制策略两方面对直驱永磁同步风力机和双馈风力机进行了仿真建模。 对于直驱机组，文献[12]，[13]指出，在故障期间直驱机组受变流器控制作用的影响， 故障电压和故障电流能很快进入到稳态，同时由于其弱馈特性， 直驱风电场发生接地故障时，其故障电流基本同相位且幅值近似相等。 对于双馈机组，文献[14]，[15]指出，其故障特征可归纳为频率偏移特性、与直驱机组类似的弱电源特性以及正负序阻抗不稳定、不相等特性，其中频率偏移特性会造成在故障期间故障电流的频率偏离工频量，如有低电压穿越能力的双馈机组风电场除三相金属性故障外， 风电场侧故障电压、电流的频率均不相同， 其电压频率由电网支撑，主要表现为工频，电流频率由故障前风机转速决定，主要表现为非工频。 文献[16]～[20]分析了基于电流突变量原理和基于电流序分量原理选相元件的风电适应性， 对于相电流差突变量选相元件，故障期间风电机组的正、负序阻抗角差不稳定且变化范围较大，导致相电流差突变量的幅值随正负序阻抗角差的变化而波动。 对基于故障电流对称分量原理的选相元件而言，风电机组在故障期间正、负序阻抗幅值的不相等、不稳定，使得风电场侧的正负序电流分支系数相差较大且不为定值，导致了故障电流序分量幅值及相位关系的不稳定。 由此可知，风电场特殊的阻抗特性会造成上述两种选相元件的选相失败。

目前，对风电接入系统继电保护的研究多集中在双馈机组，未考虑双馈风电场和直驱风电场集群并网时对常规选相元件的适应性。 考虑到送出线故障电压由系统支撑不受风电场弱馈、频偏等特性的影响，且双馈和直驱机组的弱电源特性和正负序阻抗不相等及不稳定引起的故障特征类似[10]，[20]，本文提出利用电压故障分量代替常规的电流故障分量进行故障选相。 由于电压模故障分量选相原理对于高阻接地故障不能准确判别，而保护安装处电压具有与故障点基本同相的特点[21]，所以将基于稳态电压对称分量的选相原理与基于电压模故障分量的选相原理相结合，以提高故障选相的准确性和灵敏度。 最后搭建集群风电场模型并对新方案进行仿真验证。

1 风电场送出线电压模故障分量特征分析

对电流突变量原理和电流序分量原理的分析可知， 这两种传统选相原理并不适用于拥有特殊阻抗特性的风电场送出线。 鉴于电压模故障分量选相原理可规避故障电流的不适应性， 本文主要分析集群风电场送出线上发生各类故障时， 保护安装处所对应电压模故障分量的特征， 其模型如图1 所示。

图1 集群风电场并网模型Fig.1 Model of grid-connected cluster wind farm

由图1 可知：模型左侧为风电场侧，右侧为系统侧，保护分别安装在m 和n 的两侧，Zw（j）（j=1，2，0，后文相同）和Zs（j）分别为风电场侧和系统侧的序阻抗；ZLm（j），ZLn（j）分别为送出线m 侧和n 侧的序阻抗；f 为故障点。

由对称分量法可知，f 点三相电压的故障分量可表示为

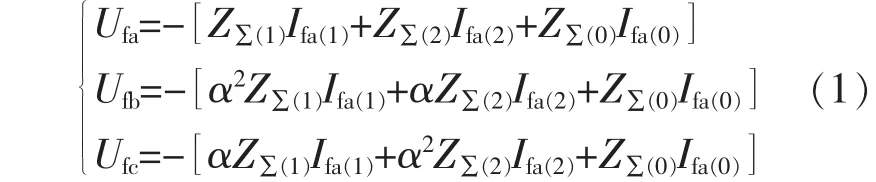
式 中：Ufa，Ufb，Ufc分 别 为 故 障 点 三 相 电 压 故 障 分量；Ifa（j）为故障点处A 相的序电流；α（α=ej120°）为旋转因子；Z∑（j）为系统的序阻抗。

本文侧重研究风电场侧保护安装处电压的故障分量特征，根据图1 可得m 侧保护安装处的电压故障分量为

式中：Uma，Umb，Umc分别为m 侧三相电压的故障分量；C（j）为各序电流分配系数。

不论在送出线上发生何种故障， 系统各点电压暂态量都可以分解成故障分量和非故障分量[22]。 为使故障分量中的暂态成分在继电保护中得到很好的利用，也为了简化参数计算，提高保护的灵敏度， 通常会利用Clark 法以及卡伦鲍厄法等来实现相模变换。 本文所使用的相模变换矩阵为

式中：U0为地模分量；U1，U2，U3为线模分量。

经式（3）的相模变换矩阵，可提取出m 侧电压故障分量的模量信息。

当系统发生单相接地故障时， 以A 相为例，G 表示接地故障，则AG 故障时其故障边界条件为

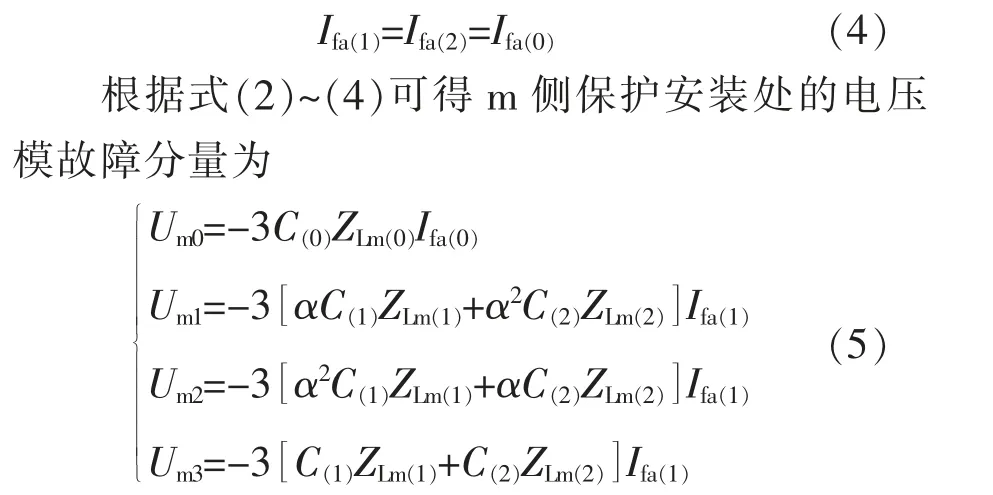
式中：Um0为m 侧保护安装处故障电压的地模分量；Um1，Um2，Um3为m 侧保护安装处故障电压的线模分量。

由式（6）可知，P1≡1，P1不受k 的影响，但P2会随k 变化，P2-k 的关系曲线如图2 所示。

由图2 可知： 当发生单相接地故障时，P2的值域为[1，2]，对于风电系统，随k 的变化，P2始终处于1～2。即风电场送出线发生单相接地故障时，有Um0≠0，并且AG 故障时有P1=1，P2∈[1，2]。 由此可知， 该电压模量的数值关系可作为AG 故障的选相判据。同理可得：BCG 故障时Um0≠0，P1=1，P2∈（0，1]；BC 故 障 时Um0=0，P1=1，P2∈（0，1]；三相短路故障时Um0=0，P1=1，P2=1。

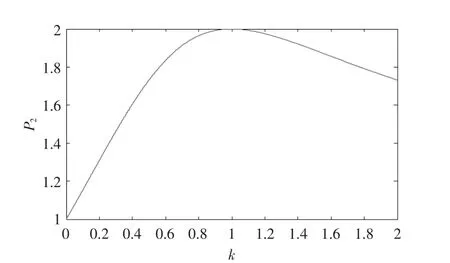
图2 P2 与k 的关系曲线Fig.2 Relation curve of P2 and k

2 风电场送出线稳态电压序分量特征分析

当大接地电阻发生接地故障， 或在较长线路末端发生故障时， 弱电源侧使用电压模故障分量的选相灵敏度并不理想， 须要结合其他选相原理来提高灵敏度。 由于保护安装处电压与故障点基本同相， 本文将基于稳态电压序分量的选相原理与基于电压模故障分量的选相原理相结合， 以此提高送出线发生接地故障时选相的灵敏度， 其模型如图3 所示。

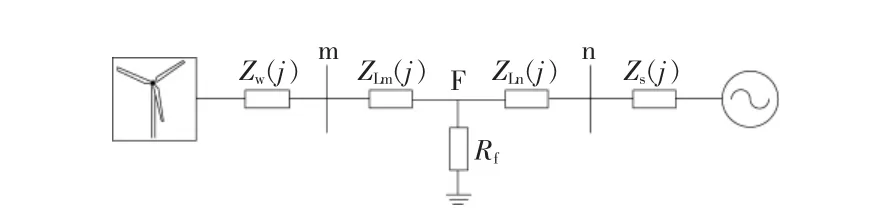
图3 集群风电场送出线经过渡电阻接地模型Fig.3 Model of cluster wind farm outgoing line through resistance grounding

图中：F 为故障点；Rf为风电场送出线上发生接地故障时的过渡电阻； 保护分别安装在m 和n的两侧。 在整个系统中，风电场属于弱电源侧，因此本文主要研究m 侧保护。 由于保护背侧风电场的正、 负序阻抗远远大于保护安装处正方向线路上的阻抗，在故障时，风电场侧母线电压和故障点电压基本同相。 设U（j）为m 侧保护安装处的各序电压；UF（j）为故障点F 处的各序电压。 定义保护安装处的分压系数为D（j），因此m 侧各序电压与F点各序电压的关系为U（j）=D（j）UF（j）。 当送出线发生故障时，风电系统正负序阻抗并不相等，即D（1）≠D（2），所以U（1）≠U（2）。由于风电场处于弱馈侧，所以受其背侧负荷阻抗的影响使得D（1）和D（2）的阻抗角较小， 又由于利用稳态电压序分量的相位关系进行选相时会有一定的角度裕度， 故而在进行电压序分量的相位关系分析时将D（1）和D（2）近似看成实数，不会对选相结果造成影响。 同时，由于风电场主变中性点接地，因此D（0）不受风电场侧背侧负荷阻抗的影响，即D（0）亦为实数。 综上可知，保护安装处的电压序分量和故障点电压序分量有着近似相同的相位关系， 只是各序电压幅值不相同， 因此在后文的分析中直接分析故障点各序电压的相位关系即可。

由单相接地故障的序网络图可知， 在不考虑过渡电阻的情况下发生单相接地故障时， 各序电压相位关系如图4 所示。

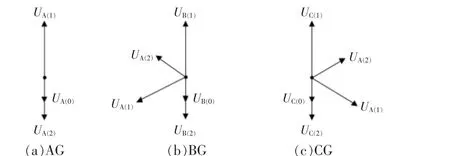
图4 单相接地时各序电压相对相位关系Fig.4 Relative phase relationship of each sequence voltage in single-phase grounding fault

整合发生单相接地故障时， 各故障相的零序与负序、正序与负序电压相位差如图5 所示。

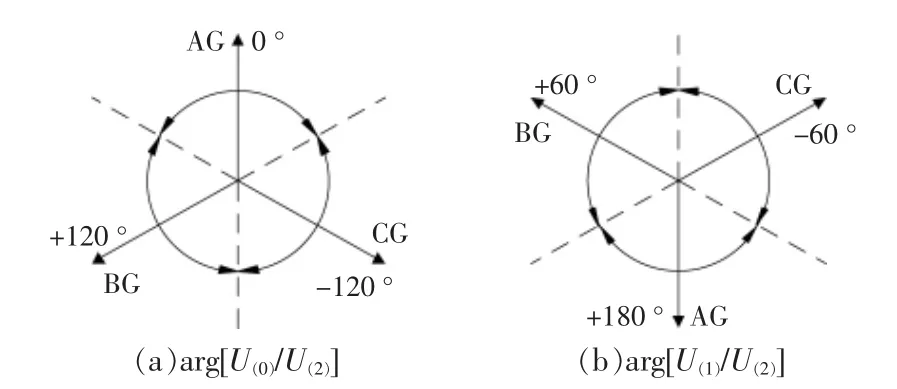
图5 不同序电压的相位差与单相接地故障的关系Fig.5 Relationship between phase difference of different sequence voltages and single-phase grounding fault

同理，由两相短路接地故障的序网络图可知，在不考虑过渡电阻的情况下发生两相短路接地故障时，零序与负序电压相位关系、正序与负序电压相位关系如图6 所示。

令α=arg[U（0）/U（2）]，β=arg[U（1）/U（2）]，在 不 考 虑过渡电阻的情况下发生接地故障时， 可由图5 和图6 整合出由α 确定的3 个区域和β 分区可确定具体的故障类型，如图7 所示。

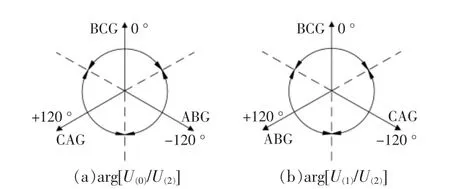
图6 不同序电压的相位差与两相短路接地故障的关系Fig.6 Relationship between phase difference of different sequence voltages and two-phase grounding fault

由图7 可知，以α 确定的A 区为例，其中AG故障在β 确定的（+90 °～+270 °）区域内，而BCG故障在β 确定的（-90 °～+90 °）区域内，其裕度角为±90 °，所以AG 的选相判据为α∈（-60 °～+60 °），β∈（+90 °～+270 °）；BCG 的选相判据为α∈（-60°～+60°），β∈（-90°～+90°）。

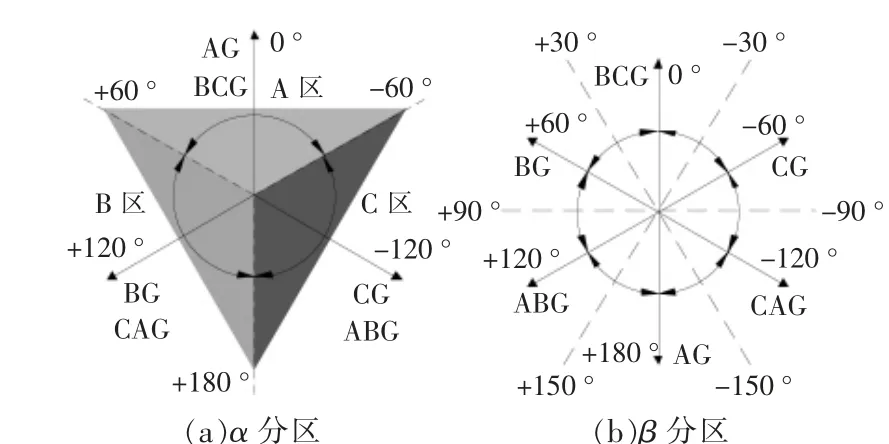
图7 接地故障与α 和β 的关系Fig.7 Relationship between grounding faults and α and β

当过渡电阻Rf发生接地故障时，由于用β 分区确定故障时有±90°的裕度，因此考虑过渡电阻亦不会影响到β 分区，从而只需对α 分区进行调整即可满足需求。对于单相接地故障，由复合序网分析可知过渡电阻不会对α 造成影响，所以重点分析两相短路经过渡电阻接地故障即可， 如图8所示。

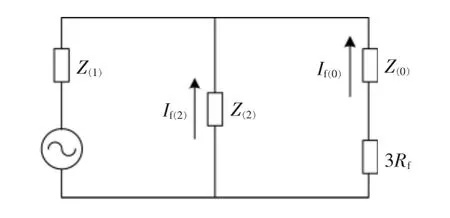
图8 两相短路经过渡电阻接地时的复合序网络Fig.8 Hybrid network of two-phase grounding fault through transition resistance

由图8 可知， 两相短路经过渡电阻接地时保护安装处的负序电压和零序电压为

由于D（0），D（2）都近似为实数，故而α 可近似等于Z（0）/[Z（0）+3Rf]的相位。 当过渡电阻为零时α=0°，当过渡电阻为无穷大时α=90°。 因此当过渡电阻在零到无穷大变化时，BCG 故障的零序、负序电压相位关系可能会超出图7 中的A 区。 现将由α 确定的故障分区整体顺时针旋转30°， 得到调整后的α 分区，如图9 所示。

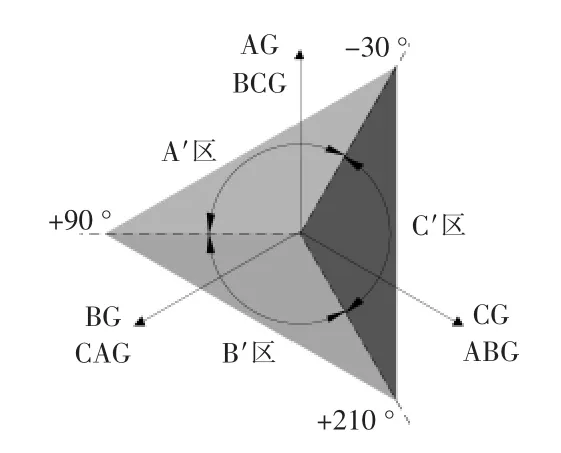
图9 调整后的α 分区Fig.9 Adjusted α partition

此时，结合调整后的α 分区和β 确定的故障分布， 即可准确地判断出经高阻接地故障的类型以及故障相。但对于风电场这样的弱馈系统，故障后风电机组的正序、负序阻抗比不确定，无法通过正序、 负序电压幅值的大小来对故障类别进行预分类，进而可能造成选相错误。 因此，将本节与上节中基于电压模故障分量的选相原理相结合，得到适用于集群风电场送出线各类故障的选相判据。

3 适用于集群风电场送出线的选相新方案

3.1 无过渡电阻时的故障特征

当集群风电场送出线上未发生经高阻接地故障时，可依电压模故障分量选相原理，将m 侧保护安装处电压模故障分量间的数值关系进行转化，进而得出故障特征。

（1）单相接地故障

3.2 经高阻接地时的故障特征

当集群风电场送出线上发生经高阻接地故障时，可依稳态电压序分量选相原理进行故障选相。根据第二节分析得出的结论可知，通过m 侧保护安装处稳态电压序分量间的相位关系与α，β 分区相匹配， 方可准确判断故障类型及故障相。 由α，β 分区确定的故障判据如表1 所示。

表1 经过渡电阻接地故障判据Table 1 Fault criterion of grounding through transition resistance

3.3 选相流程

综上所述选相判据， 可得出适用于集群风电场送出线选相新方案的流程图，如图10 所示。

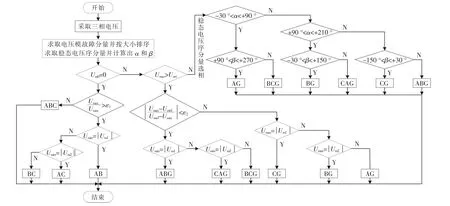
图10 集群风电场送出线选相流程Fig.10 The phase selection process of cluster wind farm outgoing line

在实际的数据提取及计算中会存在一定误差，因此流程图中的ε1需保留一定裕度，文中取1.2；Uset为判断接地故障是否经高阻接地的门槛值，可据实际情况选取，文中取0.3；ε2用来比较大小关系，文中取1。通过图10 所示选相流程，可准确判断送出线上的故障类型并选出故障相，因此该方案能够适用于集群风电场的送出线。

4 仿真验证

本文基于双馈机组和直驱机组的数学模型及运行控制策略，在PSCAD 平台搭建了含双馈风电场和直驱风电场的集群风电场电磁暂态仿真模型。 以此来模拟同一地区不同风电场就近汇集构成的集群风电场，如图11 所示。

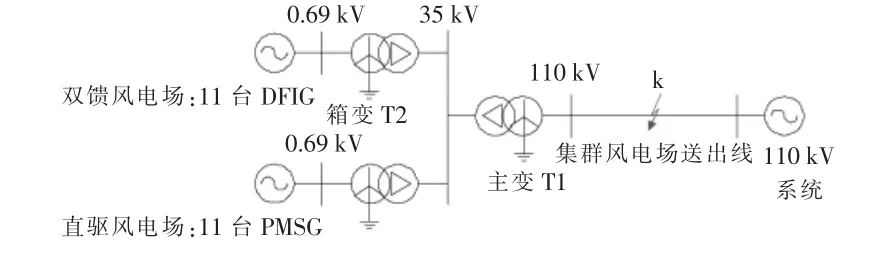
图11 含双馈和直驱机组的集群风电场并网模型Fig.11 Model of grid-connected cluster wind farm with doubly-fed and direct-drive units

图12 发生各类故障时的电压模故障分量仿真图Fig.12 Simulation diagram of voltage mode fault component when various faults occur

由图11 可知， 双馈风电场有11 台1.5 MW的双馈风力机，直驱风电场有11 台1.5 MW 的直驱风力机，机端电压均为690 V，经箱变汇集到35 kV 的低压母线，再通过主变将电压等级升至110 kV，最后经送出线连接到110 kV 系统。 其中k 为故障点， 距保护安装处100 km。 送出线总长为500 km， 其参数如表2 所示。 110 kV 主变T1 和35 kV 箱变T2 参照文献[5]中所提及的相关参数。

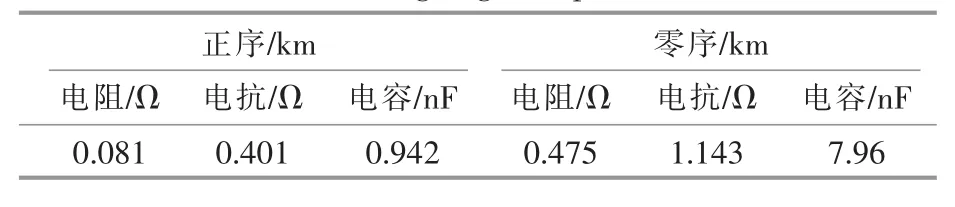
表2 风电场送出线参数Table 2 Wind farm outgoing line parameterswind farm

当设置集群风电场110 kV 送出线在k 处发生金属性接地故障或相间短路故障时，将PSCAD中得到的仿真数据导入到Matlab 中进行处理，为满足选相元件的快速性， 取故障前后40 ms 数据窗进行数据分析。 以A 相为特殊相，发生单相接地、两相短路接地、两相相间短路以及三相短路故障时，电压的故障模量如图12 所示。

将所有金属性接地故障和相间短路故障的仿 真结果整理，如表3 所示。

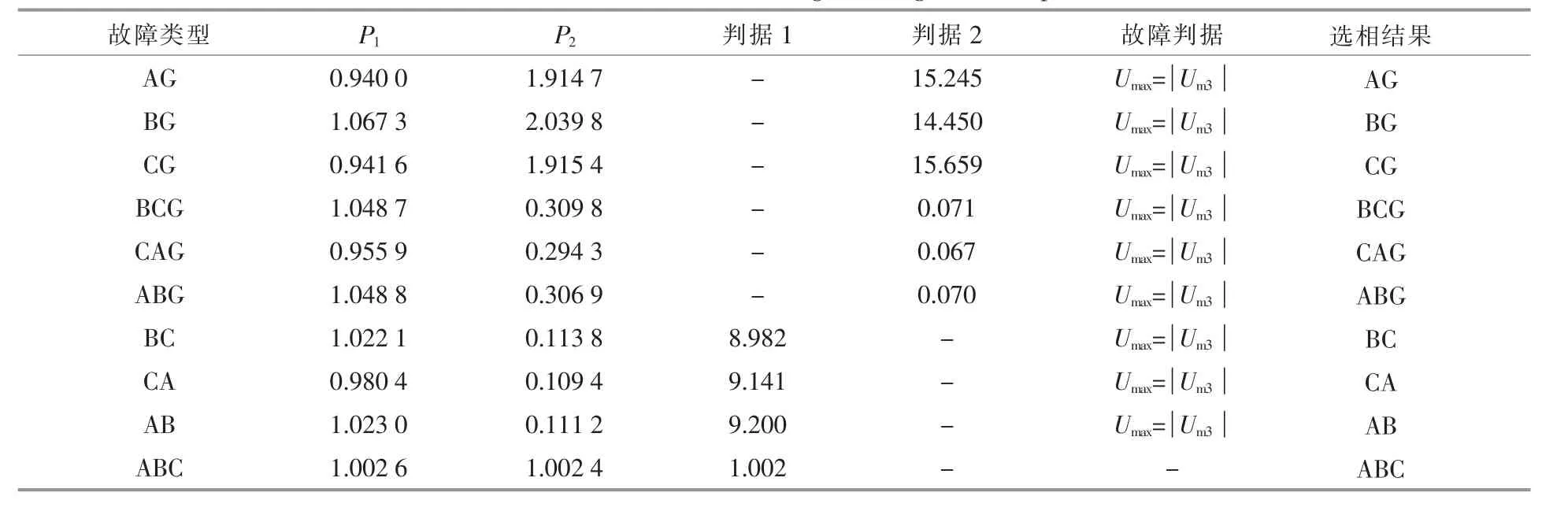
表3 金属性接地故障和相间故障仿真结果Table 3 Simulation results of fault for metal grounding and interphase short circuit

设置集群风电场110 kV 送出线，在k 处发生经高阻接地的故障时，以A 相为特殊相，基于稳态电压序分量选相原理得到的不同接地故障对应的α，β 值如图13 所示，设置系统运行4 s，在3 s时发生故障，故障维持0.3 s 后切除。

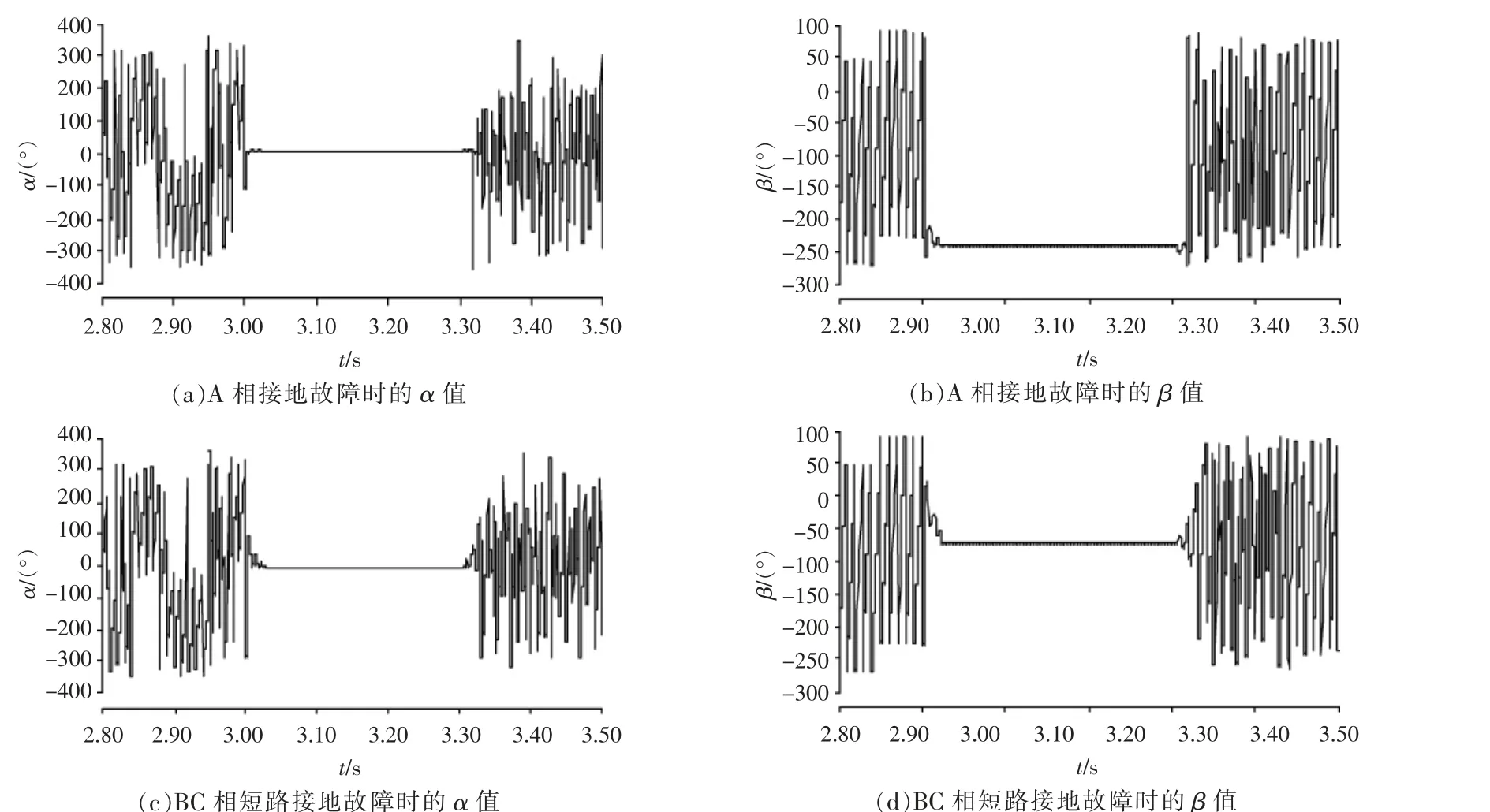
图13 k 处经100 Ω 过渡电阻发生接地故障时的α，β 值Fig.13 α，β value at the time of grounding fault at point k through 100 Ω transition resistance

由图13 可知， 当k 处经100 Ω 过渡电阻发生接地故障时， 故障相数据满足稳态电压序分量选相原理的判据。 将经过不同过渡电阻的各类接地故障的仿真结果整理如表4 所示。

由表4 可知， 当集群风电场送出线上发生经不同过渡电阻接地的故障时， 基于稳态电压序分量选相原理的选相元件可正确选出故障相。另外，本文对该选相元件在集群风电场不同运行状况和不同运行方式下的动作特性进行了仿真验证。 结果表明基于该选相新方案的选相元件在各种情况下均可准确判断出故障类别并选出故障相。

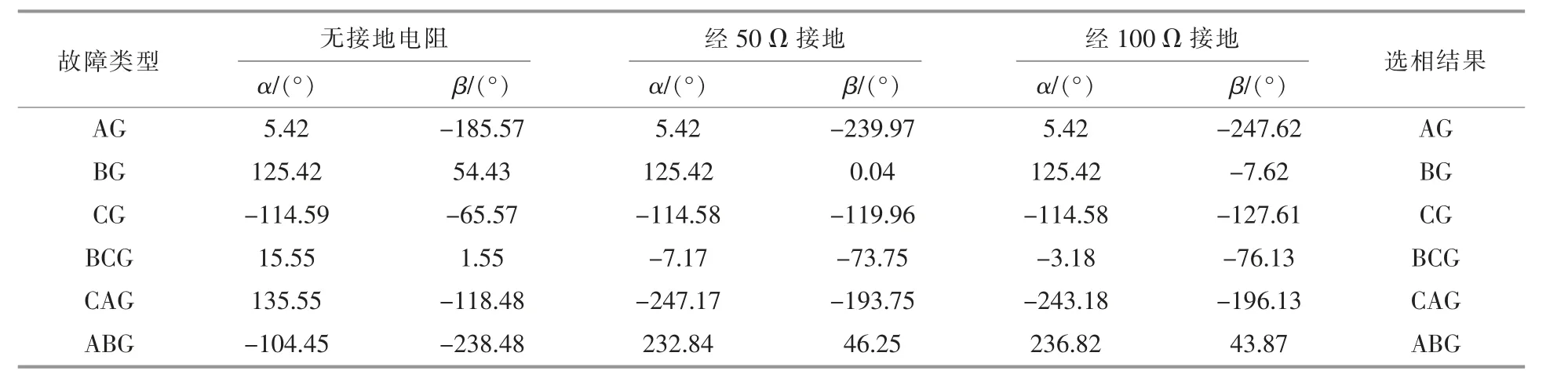
表4 经不同过渡电阻接地时的仿真结果Table 4 Simulation results of grounding faults through different transition resistance

综上可知， 基于电压模故障分量和稳态电压序分量选相原理得出的选相新方案， 可依据故障判据和选相流程准确判断出故障类型并选出故障相。 因此，该方案能够适用于集群风电场110 kV送出线。

5 结论

本文分别对基于电压模故障分量和基于稳态电压序分量的选相原理在集群风电场送出线上的应用进行了分析。 其中前者在弱电源侧具有良好的选相性能， 但对经高阻接地故障判别的灵敏度尚有不足； 而后者在弱电源侧可以准确判断经高阻接地的各类故障，但无法通过正序、负序电压幅值的大小来对故障类别进行预分类， 且序分量选相原理的复数运算较模故障分量要慢， 因此提出结合两种选相原理的优点得出新的选相方案。 该方案能够规避基于故障电流的常规选相元件在集群风电场送出线上的不适应问题， 并且可以快速准确的做出判断， 在集群风电场送出线上有良好的适应性。通过仿真可知，当集群风电场送出线上发生各类故障时， 基于该方案的选相元件均可准确判断出故障类别并选出故障相。