弹性碰撞次数与π的关联

张 伟

(重庆市万州高级中学，重庆 404120)

1 题目

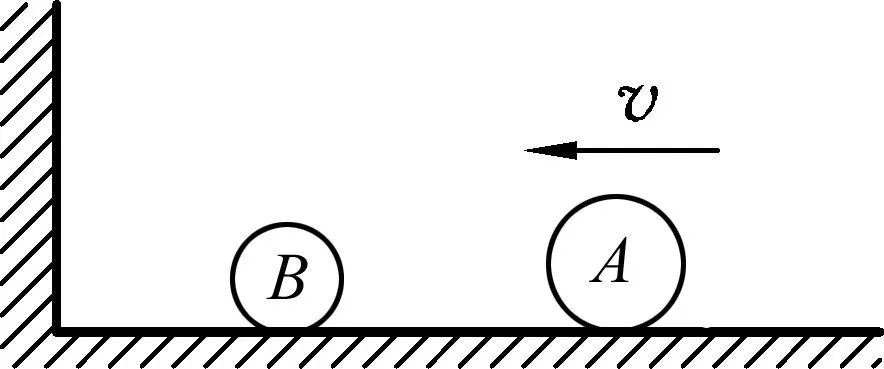
图1

如图1所示，在光滑水平面上，有一质量为M的小球A向墙运动，速度为v,A和墙之间的连线上停着另一个质量为m的小球B.假设A与B，B与墙之间的碰撞均为完全弹性碰撞，两物体可以看成质点.显然当两个球质量相等时，A碰上B，A停下来，B继续运动，B碰到墙再返回碰A.A与B、B与墙之间一共发生了3次碰撞.

如果M>m，那么小球A碰完小球B之后还会继续向墙运动，总共的碰撞次数可能会大于3.实际上，

当M=104m时，共碰撞314次;

当M=106m时，共碰撞3141次；

当M=108m时，共碰撞31415次.

随着A和B质量之比的增大，总共的碰撞次数会和圆周率的数值有关.如何解释这个关系？

2 推导分析

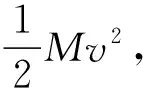
设第i次小球B与小球A碰撞后，小球B的速度为ui，小球A的速度为vi，由机械能守恒

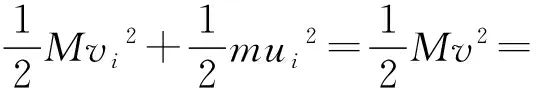
(1)

由数学知识可知，当x2+y2=C(C为常数)，满足该方程的点(x，y)在平面直角坐标系中为组成了一个圆.

设M=Nm，代入(1)式，得

(2)

将式(2)化简，得

(3)

在最开始的时候，即小球A与B第一次碰撞之前，A的速度为v，B的速度为0，在图3中用点a(v,0)来表示该状态.不妨设以向左为正方向.

图2 式(3)直角坐标系下的圆

图3 用点在圆中表示每次碰撞

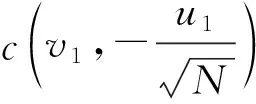
上述过程可以重复下去，直到ui≤vi时为止.此时，两个滑块都向右运动，B块追不上A，于是不会再发生碰撞.把所有的点依次用直线连接起来，如图3.

考虑A与B碰撞过程中动量守恒，假设两个小球由于碰撞前从相向而行(如图4甲)到碰撞后同向而行(如图4乙)，则

图4

Nmvi-mui=Nmvi+1+mui+1.

(4)

将式(2)两边同时除以v2,得

(5)

(6)

(7)

由和差化积公式

代入式(7)，得

(8)

化简得

(9)

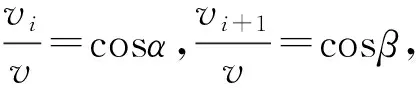
同理可得，在图5中的上半圆与下半圆每个两点之间的弧长都是定值.由式(9)，可得

(10)

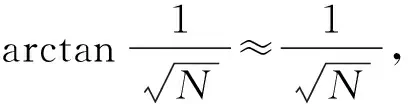
(11)

图5中上半圆中所有两点之间的弧长个数表示A与B碰撞的次数， 图5中下半圆中所有两点之间的弧长个数表示B与墙碰撞的次数，则B与A，B与墙之间的碰撞次数k，

图5 在“图3”所示的圆中表示α与β

(12)

其中[ ]表示取整.

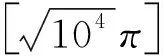
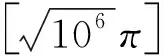
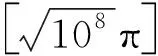
至此，问题得解.

3 结束语

通过能量守恒和动量守恒，采用圆方程和三角函数的数学手段，解释了小球间、小球与墙之间的弹性碰撞次数与π的关联.在物理竞赛教学中多和学生进行这样的分析讨论，无论对于提升学生的理论水平、分析能力，还是对于提升学生物理学习的兴趣，都能起到较大的推动作用．