基于动力有限元分析压缩机基础
——地基动力相互作用
2020-09-16李旭民
李旭民
(甘肃广播电视大学,理工农医学院,甘肃 兰州 730030)
一、前言
随着我国工业生产技术和社会经济的快速发展,高压压缩机等大中型动力设备的使用越来越广泛,压缩机使用时常常会引起振动,而任何大型设备都必须在稳定的基础上使用,因此动力设备基础的稳定性设计已成为工厂设计中的重要组成部分。否则由于设计方案不合理,过度振动严重影响设备正常工作。振动传递至基础,常常又会引起基础及地基承载能力降低。
传统动力设备基础的设计是分别计算基础和上部结构,设计工作中经常使用的设计软件也是根据该理论设计的。而实际情况是,上部结构和基础共同协作并相互影响。目前,世界各国已经对大中型机械设备基础—地基动力学之间的相互作用进行了深入地分析,主要有三个研究思路,即理论基础研究、计算分析和实验科学研究。其中,理论基础研究和计算分析基于计算机技术,而实验科学研究需要大量的经费支持,随着电子计算机和专业软件技术的进步,科研人员经常采用前两者开展科学研究。在比较研究的基础上对成果进行分析,既可以验证计算机模拟试验的可行性和测试结果的可信度,又可以验证被测实体模型的合理性,在实践中有着非常重要的意义。本文以框架式压缩发生器基础为例,研究上部结构与基础的动力特性及相互作用。
二、压缩机基础与地基动力相互作用
从振动的概念来看,压缩机基础系统的动态响应是一个开放的系统波动问题。在计算压缩机的基本动态响应时,有效模拟远距离地面介质对近场波动的影响是解决此问题的关键,引入人工边界条件并使用数值模拟技术进行计算[1]。计算区域中运动和物理边界条件的微分方程采用有限元方法,将振动波的偏微分方程简化为代数方程组运算;通过计算机模拟实现振动波的仿真。无限域中的人工边界,基础和地基之间的相关性如图1所示。
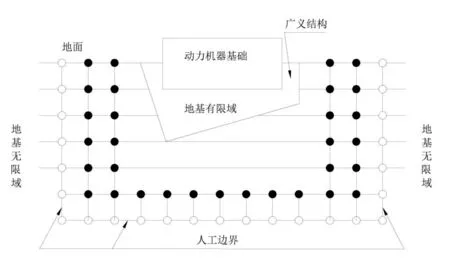
图1 压缩机基础与地基动力相互作用
从半无限介质中获取有限计算区域,考虑到压缩机基础和地基动力学的相互作用,建立了一个人工边界来模拟连续介质在切边界处的辐射衰减,最后对计算对象进行三维有限元分析。
三、结构动力学有限元分析
将无限自由度体系缩减为有限自由度体系,使有限元方法通过计算机模拟解决实际工程问题,大量的实际工程问题是用偏微分方程进行数学上的描述,把偏微分方程组的求解转换为代数方程求解,利用计算机的计算性能求解偏微分方程的数值解。在基础—地基动力相互作用分析中利用有限元法,可以将土体的性质、基础—地基间的滑移与脱开等问题综合起来。在三维有限元分析中,通常将大体积的刚性基础划分为块体元或空间梁单元,利用有限元变分法中的接触面单元模拟基础—地基的滑移与脱开。
动力有限元方法只是比静力有限元多了一个质量矩阵。
线弹性体系的结构动力平衡方程[2]为
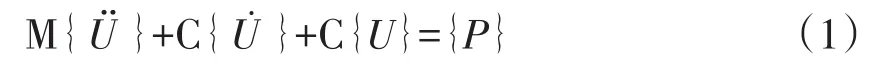
首先,假设矩阵方程式的载荷向量{P}={0},可以得到结构的自由振动运动方程式。求解方程可以确定结构的固有频率和振动模式。当阻尼相对较小时,结构的阻尼对固有频率的影响很小,因此可以进一步忽略阻尼的影响。通过求解广义特征值的结构特征方程式(2),可以求解结构的固有频率ω。

压缩机动力机械的干扰力通常是简单的谐波负载。对于谐波响应分析,属于强迫振动的频域分析,可以通过傅里叶变换法直接求解。令N组干扰力作用于机器上,j个干扰力的傅立叶变换如下
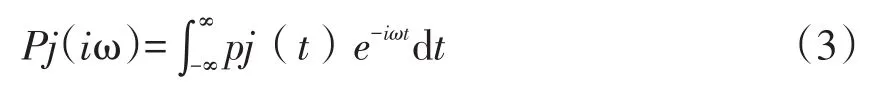
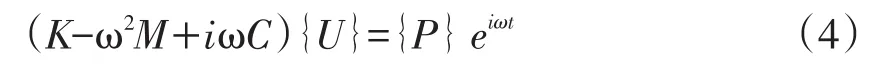
式(4)为代数方程组,其解为
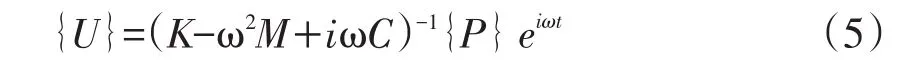
对于一般情况,当有N个相同频率扰力作用在结构上时,第j节点的振幅为各个扰力单独作用下引起的振幅叠加,即为

式(6)为复数方程式,因此各个扰力作用下的振幅分量存在相位角,应根据矢量原则进行叠加。
首先,建立单节点单元刚度矩阵和两节点单元刚度矩阵。其次,假设各层单元之间的接触条件是完全连续的,则在此条件的基础上,分别推导出单节点层单元和两节点层单元的单元刚度矩阵,然后得出单元总刚度矩阵。最后,根据具体实例,分析不同载荷频率,不同底层模量和不同层厚下土壤表面各点的垂直位移[3]。分析结果如下:
第一,土壤表面各点的位移曲线出现波动;随着底层模量和厚度的增加,土壤表面点的垂直位移曲线的波动显著减小。
第二,荷载左右两侧土体的垂直位移是对称的;随着层厚度的增加,土壤表面的最大垂直位移减小;土层厚度对荷载作用下土的竖向位移影响不大;当底层的模量达到一定值时,最大垂直位移不会明显改变。
第三,当载荷频率较低时,垂直位移从载荷中心到两侧逐渐衰减,经过多次波动后,其可恢复到接近零。否则,当载荷频率较高时,垂直位移从载荷中心到两侧都将迅速衰减,并且可以在不经历许多波动周期的情况下达到零点。
四、实例
(一)工程简介
以压缩机基础为例,基础柱有3组柱,每组有2根柱,水平柱距为4.8 m,垂直柱距为3.6 m和6 m,柱截面为0.8 m×0.8 m,屋顶高程为7 m,混凝土使用C30。
材料特性:
弹性模量E=3.0×104N/mm2,泊松比ρ=0.2,阻尼比为0.0625,密度2.5×10-9t/mm3,发电机转子质量m=9.4t,压缩机转子质量m=7.35 t,工作速度v=3000r/min,频率f=50Hz;发电机的垂直和水平总干扰力(在每个干扰点均分)为20 kN,纵向干扰力为10kN;压缩机的垂直和水平总干扰力(在每个干扰点均分)为15 kN,纵向干扰力为7.5 kN,垂直和水平干扰相差90°,而纵向和横向干扰相差相同。根据以上参数,使用ANSYS建立如图2所示的有限元模型。
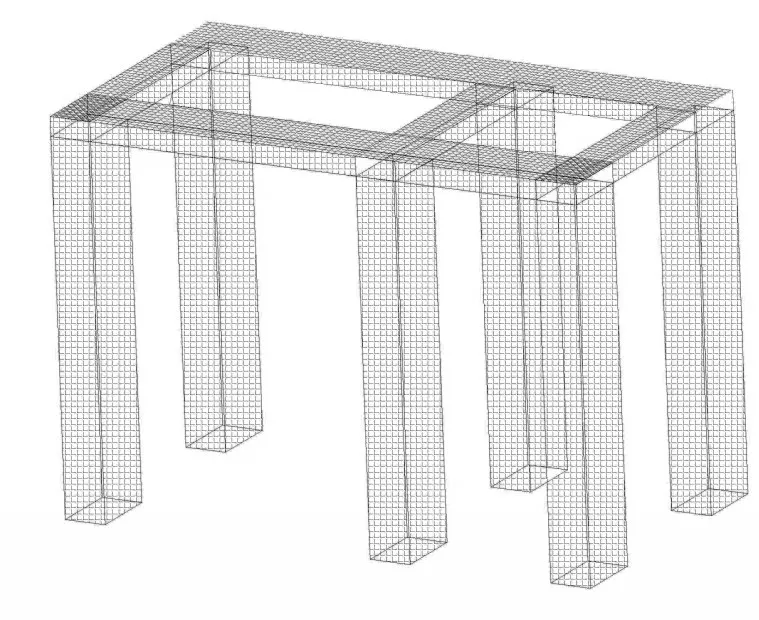
图2 计算模型
其中,压缩机被Mass21单元代替,梁和柱都被Beam188单元分散[4]。有限元模型的约束条件为柱脚是固结点。负载中包括基本重量、单位重量和设备干扰。单位设备的重量在功率计算和分析中用作附加质量。载荷施加点的位置如图3所示。图中黑色螺栓孔的位置就是载荷施加点的位置。在图3中,设备基础从左到右的动力设备是电动机和压缩机。
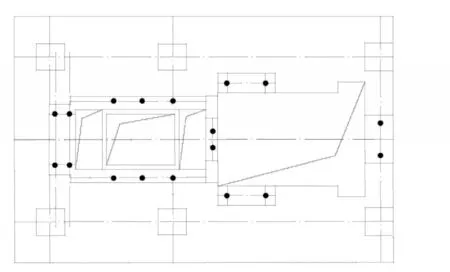
图3 荷载应用点的布局
(二)模型建立
为了研究和比较压缩机基础与地基的协同工作状况,依据具体实例考虑基础和上部的共同作用,把地基作为天然地基模拟,利用ANSYS有限元软件建立三维实体单元结构主体的压缩机基础的有限元模型,模型示意图见图4和图5。
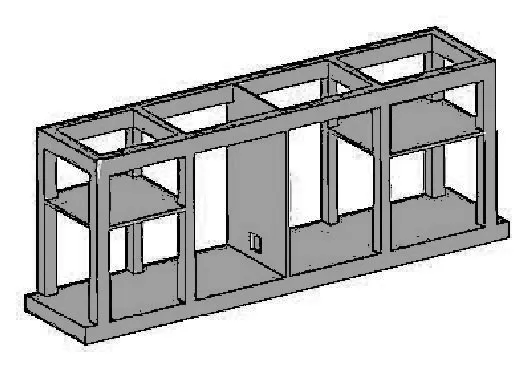
图4 结构示意图
图5 网格划分及约束示意图
(三)模态分析
为了避免共振,使用ANSYS有限元软件进行结构建模的模态分析应避开基本固有频率,因此应通过模态分析确定结构的振动特性(基频和模态)。为了使(X,Y,Z)三个方向上参与模态形状的质量达到总质量的95%以上,本分析计算了前100个阶次模态。一阶、二阶到六阶对应于沿基础结构的宽度(X方向)、长度(Y方向)和高度(Z方向)的振动效果。七阶之后,质量参与系数非常大,对结构振动的影响很小,可以忽略不计。表1列出了从1阶到6阶的基本频率。

表1 1~6阶的基本频率/HZ
(四)谐响应分析
在压缩机的启动和运行过程中,由于质心和旋转中心对不准,由压缩机转子的旋转产生的离心力被称为干扰力,并且基础在该作用下产生强制振动的干扰力。当电机以固定的频率值运行时,作用在基础上的干扰力是简单的谐波力,会根据正弦或余弦函数而变化。
在相同的计算中,水平和垂直干扰力都以简单的谐波(正弦)负载Asin(αt+φ)存在。同时,水平和垂直相角相差90°,水平和垂直幅度A相同,水平和水平相角相同。在设备运行的不同时刻,干扰力对应于不同的相位。该程序将自动计算每个时刻的水平和垂直干涉力,并将其施加到顶板上的螺栓点,如图3所示。在模态分析的基础上,进行上述动力响应分析和计算,以得出简单的谐波力。根据对原始振动线性位移计算公式的分析,计算出的垂直振动线性位移幅度始终大于两水平振动线性位移幅度,并且三个方向的允许线性位移相同。它仅用于计算需要计算干扰点的垂直振动的线性位移,垂直振动的最大线性位移应在工作速度±25%的范围内。因此,在计算期间必须将频率扫描到工作速度的±25%以内。因此,干扰力频率的扫频范围为0~65 Hz(对应于速度0~3900r/min)。在启动和运行期间,每个干扰力作用点的最大垂直振动线性位移如图6所示。
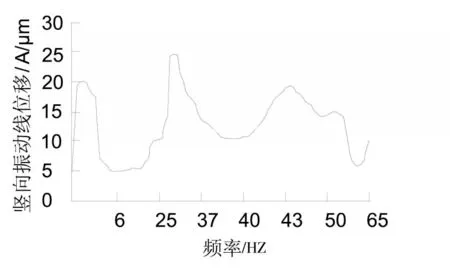
图6 基础垂直振动的线性位移
从图6可以看出,在0~37.5 Hz(小于工作速度的75%)的频率范围内,垂直振动线性位移的最大位移为25μm<1.5[A]=30μm,符合规格要求;在37.5~65 Hz的频率范围(工作速度±25%范围)内,振动线性位移的最大值为19.8μm<[A]=20μm,符合规格要求。
五、结论
对动力机械基础动力特性的研究是一个非常复杂和实际的课题。本文采用数值有限元方法对大型压缩机设备的基础进行数值计算。通过实例计算,数值方法可以较好地模拟动力设备基础的振动。考虑基础与基础之间的相互作用,有限元方法可以模拟动力设备的基础及其周围环境。与基于单颗粒模型的标准方法相比,土壤的实际工作机理具有更高的精度和可信度。数值有限元法不仅可以得到任意点的动力响应(位移、速度、加速度)的时间历程曲线,而且在垂直振动、扭转振动、摇摆振动和耦合振动的计算中具有统一性和通用性。振动类型使用不同的动态计算公式,并选择不同的计算参数。不再需要分离影响动态响应的各种因素,例如埋深、扰动形式地质条件和基本形式,从而大大简化了振动形式,计算准确性得到提高。
