页岩对CO2的绝对吸附量及其影响因素试验研究

汤积仁，张 靖，卢义玉，王相成，陈侠宇，周建坤，陆朝晖

(1.重庆大学 煤矿灾害动力学与控制国家重点实验室，重庆 400030; 2.重庆大学 复杂煤气层瓦斯抽采国家地方联合工程实验室，重庆 400030; 3.重庆地质矿产研究院 页岩气勘探开发国家地方联合工程研究中心，重庆 401120)

随着对全球气候变暖课题的持续研究[1]，CO2捕集与埋存技术(CCS)被认为是实现CO2减排，控制全球气候变暖的主要途径[2]。页岩气储层渗透率极低，对CO2拥有较强的吸附能力[3]，同时又能促进CH4的解吸提高页岩气采收率[4]，是进行CO2封存的较理想盖层[5-6]。吸附态气体占页岩储层气体总储量的20%～85%[7]，页岩储层对CO2的吸附能力是决定CO2能否长期稳定封存的重要因素之一，因此开展页岩储层对CO2吸附能力的研究势在必行。

2013年，美国能源部部署7个“区域碳封存伙伴关系(RSCPs)”研究和发展CO2封存技术[8-9]。国内外学者研究得出CO2在页岩储层中有3种存在形式[1,10-11]:① 自由状态处于孔隙、裂隙中;② 溶解状态处于岩层流体中;③ 吸附状态存在于有机质孔隙、黏土矿物中。本文主要研究以状态③ 存在于页岩中的CO2含量。

JONATHAN S等[12]研究指出，页岩层存封CO2能力与地层厚度、孔隙度、有基质丰度等相关。KANG S M等[13]对页岩进行三维孔隙建模，将进入页岩孔隙网络的CO2分为吸附状态和自由状态两部分，模拟得出:在页岩有基质孔隙中，吸附状态的CO2占97%以上，页岩对CO2吸附能力与平衡压力呈Langmuir关系。MICHAEL等[14]对美国Marcellus Shale储层CO2封存能力进行模拟计算得出吸附状态的CO2封存能力达0.92 Mt/km2，但未从Gibbs吸附的角度分析其吸附行为。周来等[15]考虑煤的体积变形对煤过剩吸附量的影响，提高了过剩吸附量的拟合效果，但未对绝对吸附量进行研究。周尚文等[16]阐明了页岩吸附CH4过剩吸附量与绝对吸附量的差异，且考虑吸附相体积对绝对吸附量的影响并对其进行了校正，但忽略了页岩的体积应变对绝对吸附量的影响。故国内外研究以过剩吸附量为主，对绝对吸附量研究较少，且只考虑了吸附相体积对绝对吸附量的影响，因此为了准确计算页岩对CO2的绝对吸附量，应综合考虑多方面因素对绝对吸附量的影响。

基于上述，笔者从Gibbs吸附的角度分析，研究页岩对CO2吸附能力，在前人研究基础上，综合考虑吸附相体积和试件体积变形量对吸附系统自由空间体积的影响，推导绝对吸附量计算模型，研究页岩对CO2的绝对吸附量并对影响其绝对吸附量的因素进行分析，并对深入探索CO2提高页岩气采收率(CO2-EGR)技术提供参考。

1 试验样品特征

试验页岩样品取自四川宜宾市下志留统龙马溪组页岩，已测得5组样品平均有机碳含量(TOC)、镜质组反射率(Ro)和孔隙率分别为3.45%,2.54% 和3.91%，均满足我国页岩气储层核心评价标准[17]。已测得页岩样品矿物分析结果见表1，孔隙特征如图1所示。

2 试验设备及方案

2.1 试验设备及方案

试验设备为重庆大学自主研发的“高温高压页岩吸附膨胀仪”。主要由恒温水浴系统、主体试验系统、应变测量系统、数据采集系统4部分组成，系统原理图如图2所示。恒温水浴系统控温在5～95 ℃，控温精度±0.5 ℃，内设循环水泵保证整个水浴温度的均匀和平稳。主体试验系统置于恒温水浴中，主要由参考室、吸附室、温度传感器(美国Omega公司PR-21系列，精度±0.15 ℃)、压力传感器(美国Omega公司PX-409系列，量程0～24.13 MPa，精度为满量程的0.03%)等构成。利用此设备可实现不同温度条件下单组分气体煤岩(粉末)等温吸附试验、多组分混合气体煤岩(粉末)等温吸附试验、块状煤岩吸附-解吸及变形试验等。

图2 试验系统示意Fig.2 Schematic diagram of test equipment

试验过程中，试验气体通过增压泵(美国Teledyne ISCO公司260D系列)注入参考室，待气体温度稳定至设定温度后打开参考室与吸附室间的阀门，气体进入吸附室。应变测量系统通过应变仪(东华DH3818型，量程19 999×10-6，准确度为示值的0.5%)实时采集电阻应变片应变数据。

研究表明，我国页岩气储层平均埋深约为3 000 m[18]，地层温度、压力条件能够达到CO2临界状态(31.04 ℃，7.38 MPa)。因此本文所有试验均在35 ℃恒温条件下完成。

笔者使用CO2气体对3组页岩试样进行等温吸附-变形试验，试验流程如图3所示。实验过程中受试验设备精度影响，确定以0.3 h内应变值保持稳定为变形达到平衡的标志，以1.0 h内气体压力下降值小于压力传感器精度(0.007 MPa)为吸附平衡标志，即认为此时吸附速度和脱附速度相等，表观吸附速度为0，达到吸附平衡。

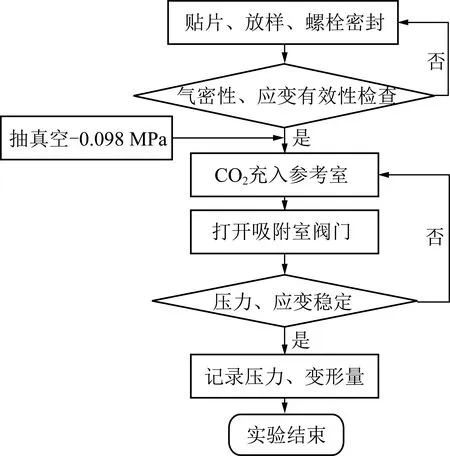
图3 吸附试验流程Fig.3 Procedure of adorption test

2.2 试验过程

2.2.1试件制备

从同一块页岩垂直层理方向取φ50 mm×100 mm圆柱试件。在打磨机上将其两端磨平，依次用180，600，1 000，2 000目的砂纸将试件表面打磨光滑，放入恒温箱中干燥24 h。测量试件尺寸、质量(电子天平FA 2004型)后将试件放入密封袋中保存备用，经打磨处理后的试样如图4所示。

图4 试验样品Fig.4 Test samples

2.2.2试验准备

检查试验装置气密性。向参考室、吸附室中注入17 MPa氦气，恒温状态下保压12.0 h,平均1.0 h内压降不超过压力传感器的精度(24×0.03% MPa)视为气密性良好。用He气两阶段压力平衡法标定吸附室体积。

2.2.3试验过程

(1)从密封袋取出试样，沿径向、轴向用胶水各贴两片应变片，待胶水凝固后将应变片连接至应变采集仪。将装入试样的吸附室密封后放入35 ℃恒温水浴中，接好各气体管路。对吸附系统抽真空至相对真空度稳定至-0.098 MPa。

(2)静置24 h使主体试验系统和吸附室中样品充分受热。

(3)先向参考室充入一定量的CO2气体，压力稳定后打开参考室与吸附室间的阀门，进行等温吸附试验，直至吸附平衡。

(4)陆续升高CO2气体压力，重复步骤(2),(3)直至平衡压力达16 MPa。

3 试验结果及分析

3.1 页岩绝对吸附量计算模型

MASTER K J等[19]根据吉布斯吸附相的定义，提出气体绝对吸附量计算式为

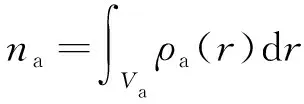
(1)

式中，na为绝对吸附量;Va为吸附相体积;ρa为吸附相密度;r为吸附相与固体相表面的距离。

将吸附相密度取平均值ρad后式(1)可化简为

(2)

式中，nap为过剩吸附量;ρg为不同压力点下实验气体的密度。

式(2)为计算绝对吸附量经验公式，这种计算方法未考虑吸附相体积和试件体积变形对吸附系统自由空间体积的影响。

现在考虑吸附相体积，及试件体积变形对自由空间体积的影响，对页岩绝对吸附量推导如下。

基本参数:CO2物质的量为M，页岩样品质量为m,体积为V，吸附室、参考室体积为Vx,Vc。设第i-1(i≥2)次吸附平衡时，主体相压力为Pi-1，吸附室内主体相密度为ρi-1，CO2吸附相体积为Va(i-1),试件体积应变为εi-1；再次注入CO2后达到第i次吸附平衡时，参考室密度为ρci，吸附平衡后主体相压力为Pi，密度为ρi，吸附相体积为Va(i),试件体积应变为εi，吸附量为na(i)。

对比学者们对吸附相密度的研究[14,20-21]，笔者采用Van der Waals气体状态方程中体积修正项b值计算单组分气体吸附相密度值:

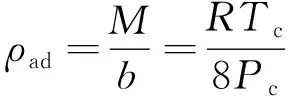
(3)

式中，Tc为气体临界温度;Pc为气体临界压力;R为气体状态常数，取8.314。

得到CO2吸附相密度ρad为1 028 kg/m3。第i次吸附平衡过程中注入的CO2气体质量:

Δmi=Vc(ρci-ρi-1)

吸附过程开始前系统主体相和吸附相的总质量:

Mi-1=ρi-1[Vx+Vc-V(1+εi-1)-

Va(i-1)]+ρadVa(i-1)

吸附达到平衡后系统主体相和吸附相的总质量:

Mi=ρi[Vx+Vc-V(1+εi)-Va(i)]+ρadVa(i)

由质量守恒原理有

Mi=Mi-1+Δmi

联立得到压力Pi处吸附相体积:

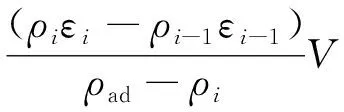
(4)

其中，ΔV=Vx+Vc-V。则压力Pi处CO2绝对吸附量na(i)为

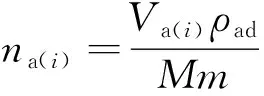
(5)

将式(4)代入式(5)，得到Pi处页岩绝对吸附量计算式:

(ρad-ρi-1)Va(i-1)+[(ρiεi-ρi-1εi-1)V]}

(6)

运用式(4)可迭代计算各平衡压力下页岩吸附相体积，将式(4)结果代入式(5)得到各平衡压力下页岩对CO2的绝对吸附量计算模型式(6)。

观察发现式(6)由3部分构成，分别体现了新注入气体质量Δm(因素1)，压力点Pi-1处吸附相体积Va(因素2)，以及试件体积应变ε(因素3)对压力Pi处绝对吸附量na(i)的影响。

3.2 绝对吸附量与CO2压力关系

试验测得应变与压力和时间的关系如图5所示。由图5可以看出，页岩在不同CO2压力的作用下具有相似的变形趋势，即变形大致可以分为3个变形阶段:短暂压缩阶段,缓慢膨胀阶段,变形稳定阶段。

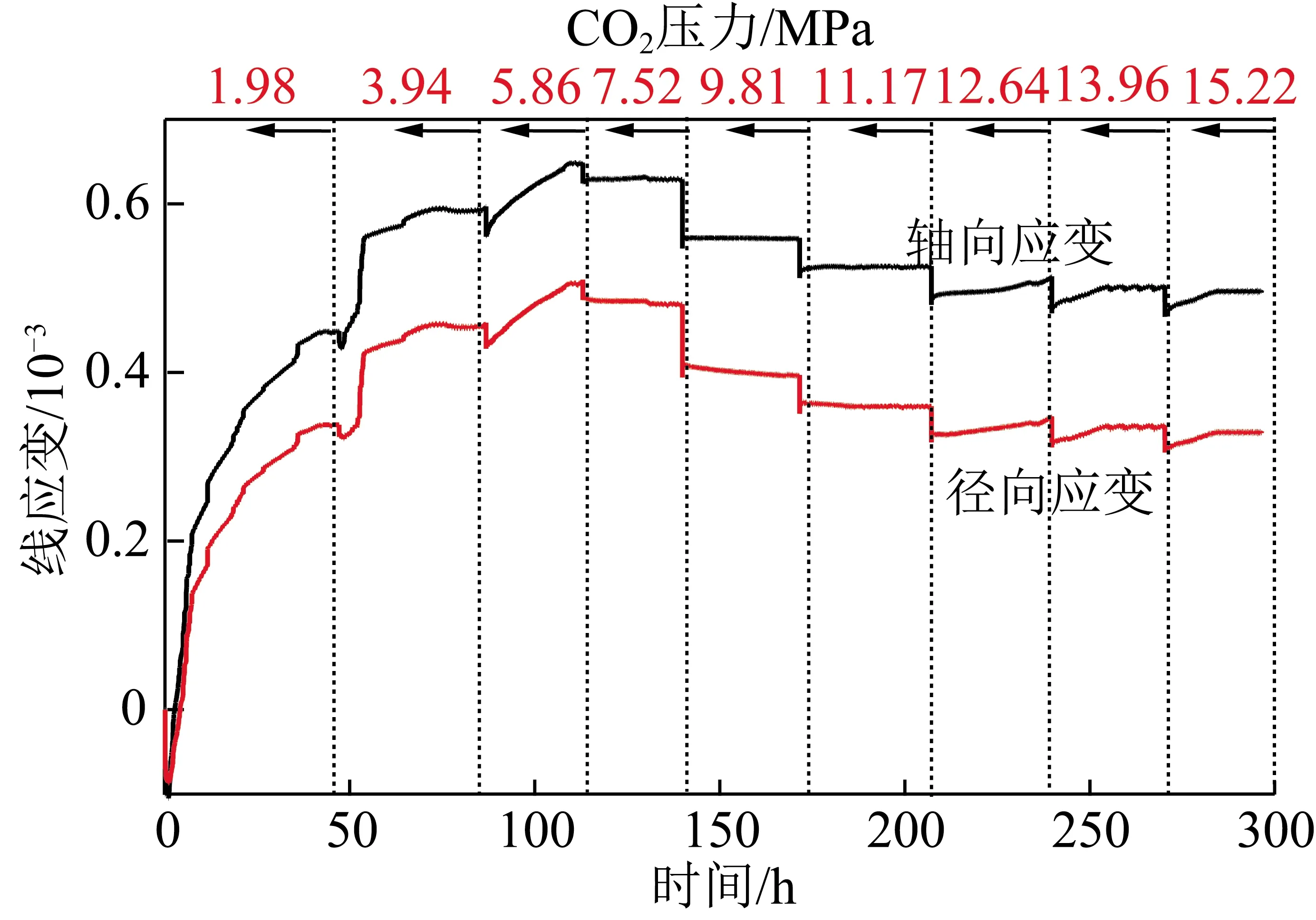
图5 页岩吸附CO2的线应变与压力和时间的关系曲线Fig.5 CO2-induced linear strain on shale as function of time and pressure

为探讨各压力条件下达到吸附平衡所需要的时间，测得3组页岩试件吸附平衡实验结果如图6所示，在CO2压力为0.86～9.43 MPa，页岩的吸附平衡时间为8.4～22.8 h。页岩对CO2吸附平衡时间随CO2平衡压力升高呈现:吸附平衡时间在0.86～6.27 MPa内随着平衡压力升高而增加;当CO2平衡压力达到临界压力附近时，平衡时间急剧减小，7.36 MPa时平衡时间最短，为9.3 h;继续升高平衡压力，吸附平衡时间再次增加。

图6 吸附平衡时间-CO2压力关系曲线Fig.6 Relationship between adsorption equilibrium time and CO2 pressure

由3.1节式(6)可知，计算页岩对CO2绝对吸附量na需要的参数有页岩试样基本物理参数、各平衡压力下CO2密度、及各平衡压力下体积变形量ε。

CO2密度ρci,ρi-1,ρi为压力和温度的函数，采用国际标准技术研究所(NIST)提供的方法计算。试件体积变形量ε由平行层理、垂直层理方向线应变εx，εy计算，采用文献[22]的计算方法，有

ε=2εx+εy

(7)

其中，ε为体积应变;εx为轴向应变;εy为径向应变。膨胀变形值为正，压缩变形值为负。

但是受页岩基质非均质性，应变片未严格按垂直、平行层理方向布置等因素影响，页岩应变测量值εx，εy存在一定误差。为使页岩体积应变计算结果更具代表性，运用敖翔等[23]对页岩体积应变与CO2密度满足SDR模型的研究成果，将3个试件体积应变、CO2密度数据代入SDR模型进行拟合，并采用拟合值对体应变测量值进行修正，使体积应变数据更接近实际值。SDR模型如式(8)所示，经拟合发现试验数据与模型有较高拟合度，拟合结果如图7和表2所示，具体拟合参数见表2，R2为相关系数，表征试验数据与拟合函数之间的吻合程度；D代表页岩吸附CO2的膨胀系数；K为CO2在页岩上的可溶解度。

ε=εmaxe-D[ln(ρad/ρi)]2-Kρi

(8)

其中，εmax为理想状态下的最大变形量。为研究CO2绝对吸附量与平衡压力的关系，将上述计算结果代入式(6)，得到3个试件在各CO2平衡压力下的CO2绝对吸附量na(i)。分别使用多项式函数、Langmuir函数、指数函数对CO2绝对吸附量数据拟合，结果见表3。

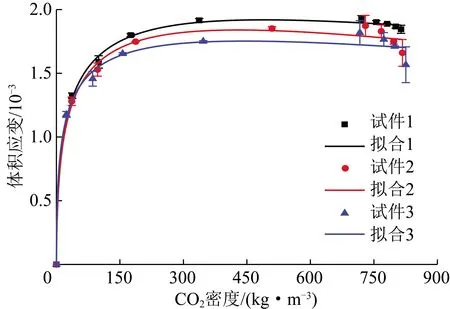
图7 页岩体积变形量拟合Fig.7 Fitting of volume deformation curve

表2 三试样体积应变拟合结果Table 2 Volume strain fitting results of three samples

表3 CO2绝对吸附量与平衡压力P关系Table 3 Functions between CO2 absolute adsorption capacity and equilibrium pressure

对比表3分析可知，在测压范围内,用指数函数表达CO2绝对吸附量与平衡压力关系时R2达到0.974 8，相对较为合理，拟合结果如图8所示。

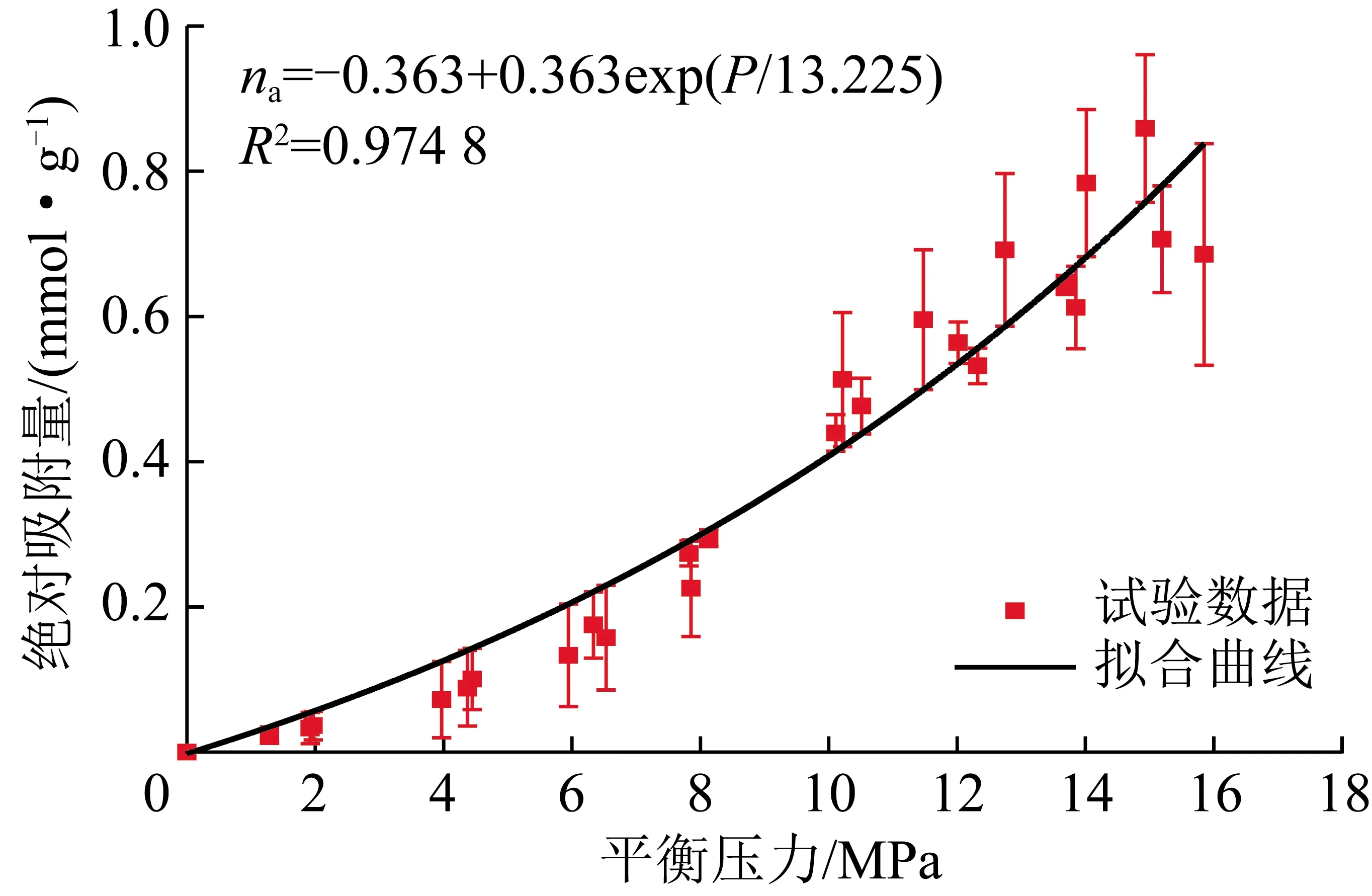
图8 CO2绝对吸附量与平衡压力关系拟合Fig.8 Fitting curve between absolute adsorption of shale and the pressure of CO2

3.3 CO2绝对吸附量影响因素分析

为进一步分析页岩对CO2绝对吸附量的构成及影响因素，根据式(6)的结构特点将na(i)分解为由注入系统CO2质量增量因素(因素1)、压力Pi-1处吸附相体积因素(因素2)、试件体积应变因素(因素3)3者引起的CO2吸附量叠加而成。对本次试验的3组试样，分别计算这3个因素所引起的吸附量，和CO2视吸附量，并将试验实测数据代入学者MASTER K J提出的式(2)计算CO2绝对吸附量，与本文计算结果进行对比，结果如图9所示。

由图9可知，使用学者MASTER K J提出的方法计算出的CO2绝对吸附量，在数值上与因素1所引起的吸附量十分接近，而MASTER K J的计算方法正是未考虑吸附相体积和试件体积变形两个因素对吸附系统自由空间体积的影响而得出的，这印证了本文在只考虑因素1时而得到的CO2绝对吸附量的准确性。吸附达到平衡过程中CO2吸附相体积的增加，页岩试件的体积膨胀变形都将导致吸附系统中主体相的体积(自由空间)减小，因此忽略因素2、因素3的影响而计算出的CO2的绝对吸附量仅在吸附相体积Va和试件变形量ε均十分微小的低压阶段较准确，在Va和ε对主体相体积影响较大的高压阶段将产生较大误差。由图9可以看出，本文的绝对吸附量计算结果，CO2视吸附量以及MASTER K J计算结果，3者在CO2压力低于4 MPa时较接近，3者差值随平衡压力升高而逐渐变大。使用本文推导的公式计算CO2绝对吸附量时对3个影响因素进行了全面考虑，更接近绝对吸附量的真实值。

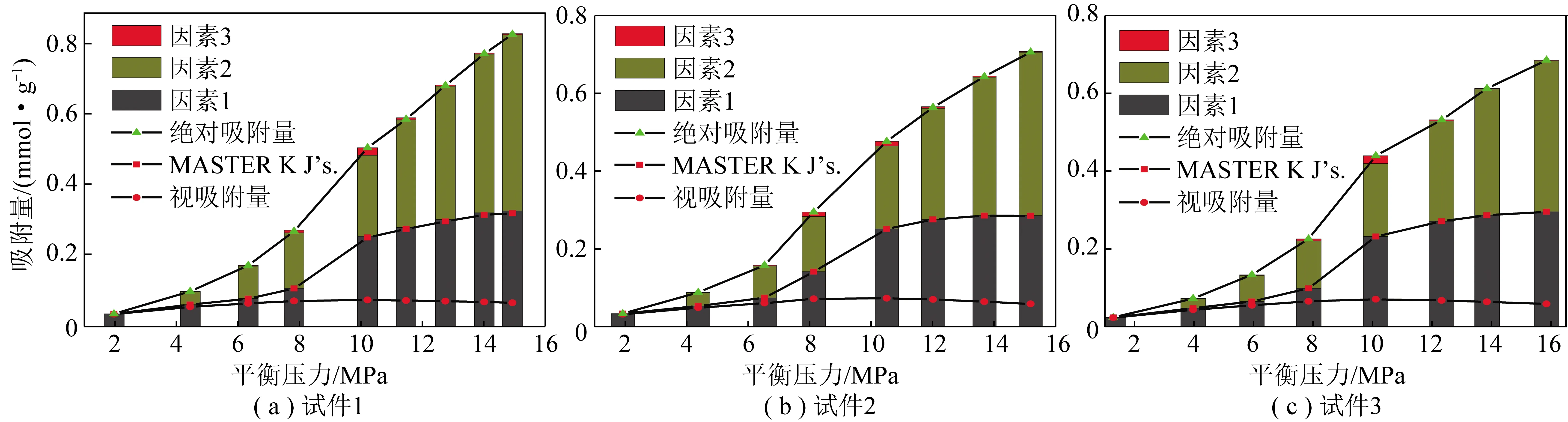
图9 页岩CO2绝对吸附量组成结构Fig.9 Components of absolute adsorption of CO2 on shale samples

试件在压力Pi-1处达到吸附平衡后，要在更高压力Pi处达到新的吸附平衡，在35 ℃恒温条件下，只有向吸附系统注入新的CO2气体才能实现主体相升压，进一步发生吸附作用，可见因素1是绝对吸附量增加的根本动力。吸附相体积(因素2)和试件体积应变量(因素3)随CO2平衡压力的升高而不断变化，直接引起主体相体积改变，间接导致CO2绝对吸附量的改变。

图10为平衡压力下由因素1、因素2、因素3所引起的吸附量占总CO2绝对吸附量的百分比。可以看出，因素1对绝对吸附量na的影响随平衡压力的升高而不断减小，因素2对na的影响随平衡压力升高不断增加，因素3对na的影响随平衡压力升高先增大后减小。

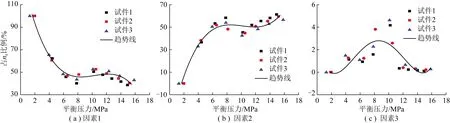
图10 各因素引起的吸附量占CO2绝对吸附量比例Fig.10 Ratio in CO2 absolute adsorption amount of each factor

因素1是导致页岩对CO2绝对吸附量na增加的根本动力，CO2注入系统后首先使主体相压力升高，促使CO2分子进入页岩深部孔隙发生吸附作用，观察图11可知，CO2注入量与因素1引起的吸附量增加量随平衡压力升高呈现出相似的变化规律，且na增加量与CO2注入量间呈线性相关。CO2注入量在8～10 MPa急剧增加是由于CO2密度在此压力范围内急剧升高所致。

图11 CO2注入量与吸附量增量关系Fig.11 Relationship between CO2 injection and adsorption capacity increment

为比较因素1、因素2对CO2绝对吸附量的影响程度，将各平衡压力下由因素1和因素2所引起的吸附量增量进行对比，如图12所示。由图12可知，CO2吸附相体积随平衡压力升高快速增加，主体相体积快速减小，造成CO2绝对吸附量na增加。综合比较可印证图10中因素2对CO2绝对吸附量的影响在Pi>6 MPa后将逐渐处于主导地位。

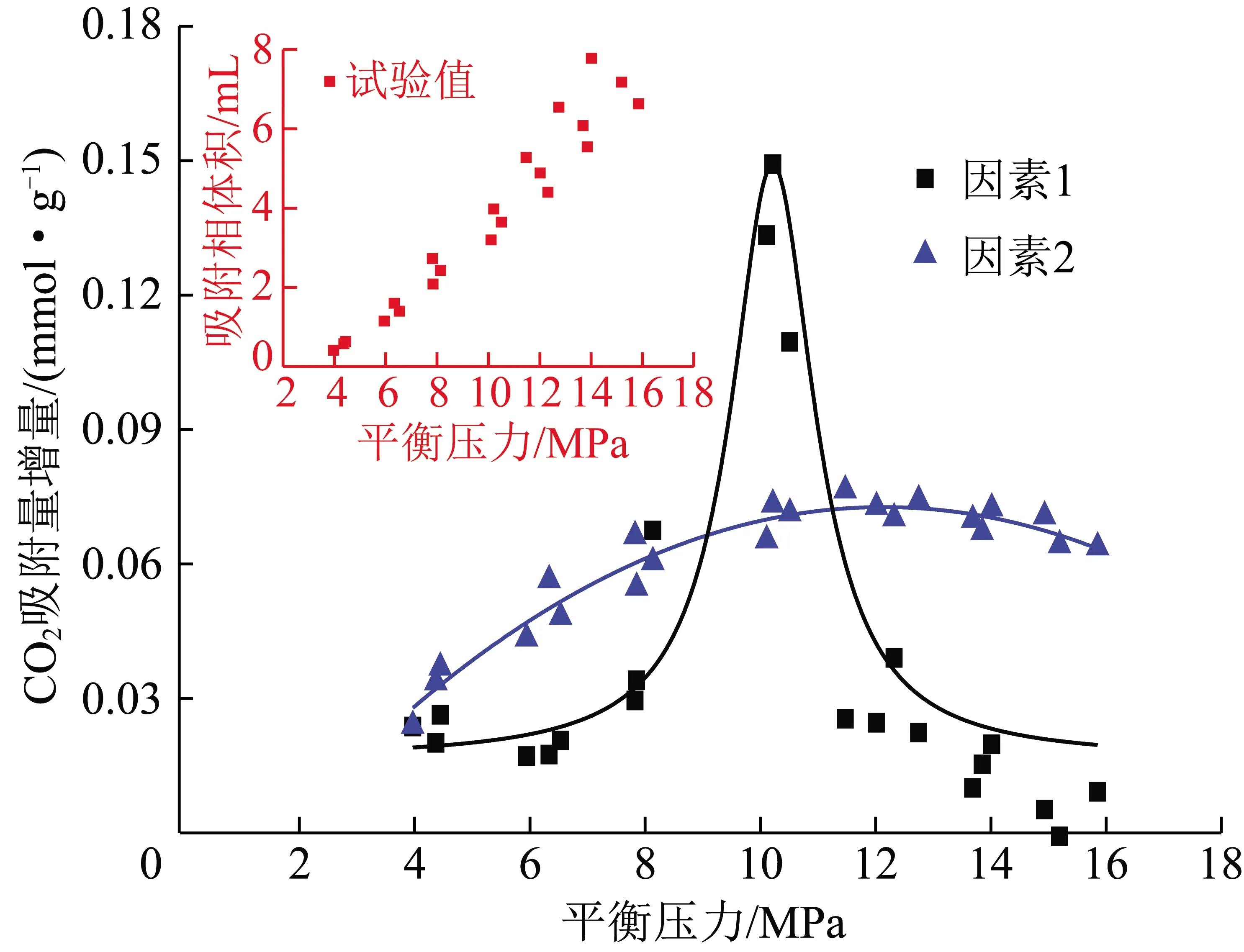
图12 因素1，2引起的CO2吸附量增量对比Fig.12 Effects on CO2 adsorption increment of factor one/two

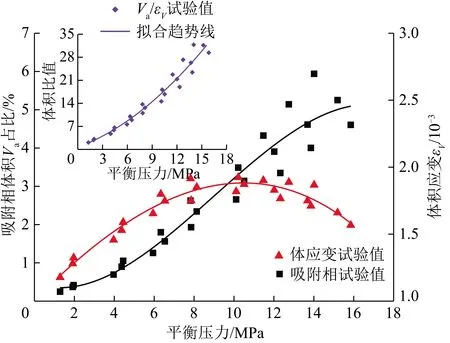
图13 因素2，3对主体相体积影响对比Fig.13 Effects on CO2 main phase volume of factor two/three

因素2,3均是通过“压缩”主体相体积的原理来影响绝对吸附量的，因此可对比吸附相体积与页岩体积变形量来分析2者对CO2绝对吸附量na的影响程度。页岩吸附相体积、体积应变与平衡压力关系如图13所示。吸附相体积随平衡压力升高不断增大，在Pi>10 MPa时可达页岩试件体积的3.5%以上;而页岩体积应变最大不足页岩试件体积的0.2%，相同平衡压力下CO2吸附相体积是页岩体积变形量的4～30倍，导致因素3所引起的吸附量占CO2绝对吸附量的比例不足5%。但对其他吸附质如煤而言，吸附CO2产生的体积变形量可达试件体积的10%，此时因素3将对CO2绝对吸附量na产生较为显著的影响。这为进一步准确计算CO2绝对吸附量从而评价CO2地质埋存能力提供重要参考。

4 结 论

(1)考虑吸附相体积和试件体积应变对吸附系统自由空间的影响，推导了适应于“阶段平衡法”的CO2绝对吸附量计算模型。模型显示页岩对CO2的绝对吸附量主要由3部分构成，分别受注入系统的CO2质量Δmi(因素1)，压力Pi处吸附相体积Va(i)(因素2)和试件体积应变量ε(因素3)3个因素影响。

(2)平衡压力低于4 MPa时，页岩对CO2绝对吸附量与CO2视吸附量相差较小，压力高于4 MPa后页岩对CO2的绝对吸附量远高于CO2视吸附量;使用多种函数对CO2绝对吸附量与平衡压力关系进行拟合，结果显示，页岩对CO2绝对吸附量与平衡压力间呈良好的指数函数关系:na=-0.363+0.363exp(P/13.225),R2=0.974 8。

(3)由因素1、因素2引起的吸附量占CO2绝对吸附量的95%以上，由因素3引起的吸附量占CO2绝对吸附量比例不足5%。随CO2平衡压力升高，因素1所引起的吸附量占na的比值呈下降趋势，其对CO2绝对吸附量的影响逐渐减弱;吸附相体积的快速增长使得因素2逐渐成为影响na的主导因素;由于页岩体积应变量十分微小，最大不足页岩试件体积的2.0‰，因此因素3对na的影响较小。