基于欧拉方法的2 维翼型冰晶结冰数值计算
2020-09-16谭燕
谭 燕
(中国民用航空飞行学院航空发动机维修培训中心,四川广汉618307)
符号表

0 引言
自20 世纪90 年代以来,全球已经发生超过100起由于冰晶造成的航空发动机功率损失事件[1-4]。航空发动机冰晶结冰问题已经受到各国重点关注,其中美国国家航空航天局(NASA)和加拿大国家研究委员会(NRC)在该方面的研究走在世界最前沿[5-8]。由于试验方法的局限性,学者开始利用数值手段进行机理研究。冰晶结冰数值模拟基本与过冷液滴结冰模拟一致,大致可以分为流场计算、粒子轨迹计算和冰形生长计算。其中,粒子轨迹计算分为拉格朗日方法[9-10]和欧拉方法[11-12]。Villedieu 等[9]开发了ONERA 2D 工具包,考虑了冰晶球度对轨迹的影响,以及冰晶反弹等因素的影响,并用NASA-NRC 的试验结果与计算结果进行了对比;Zhang 等[10]建立了冰晶反弹破碎模型和混合相模型,通过用户定义函数(User Defined Function,UDF) 方式利用 Fluent 软件模拟了NACA0012 冰晶结冰过程;而Norde 等[11]和Nilamdeen等[12]则采用计算量更少的欧拉方法计算了NACA0012冰晶结冰过程,并均与试验进行了对比。总体而言,冰晶结冰研究成果相对于过冷液滴结冰的少很多[1]。
本文采用欧拉方法对某对称楔形翼型结冰过程进行数值计算,数学模型中考虑了相变、粒子反弹等问题;采用NASA-NRC 试验结果验证了本文方法的可行性,并分析了压力、CLWC/CTWC等因素对结冰的影响。
1 模型
由于本文多相流计算中微粒浓度PL<0.1(Particulate Loading,PL=αdρd/αcρc),可以认为载体相对分散相的影响是单向的。因此,本文通过基于Spalart-Allmaras 湍流模型[13]计算出空气流场,将计算结果作为已知条件用于冰晶控制方程的计算,利用Messinger 模型进行冰形生长计算。
1.1 粒子运动和相变控制方程
由于混合相是冰晶结冰的必要条件[1,5,9],体积分数α 由固相αi和液相αw组成,故动量守恒方程由原来1 个增加至2 个

虽然基于欧拉方法的冰晶结冰计算步骤与过冷液滴结冰计算步骤相同,但冰晶在运动过程中存在质量、能量、相态的变化,因此,原有的质量和能量控制方程[14]不再适合,必须在守恒方程中考虑传质和传热问题。
当T<Tm时αw=0,冰晶完全为固相

质量守恒方程(式(3))等号右边为升华造成的冰晶质量损失,而能量方程(式(4))等号右边分别为对流和升华造成的能量转化。
当T=Tm时α=αi+αw,冰晶粒子内部为固态,而外部为液态,混合相粒子通过换热获得的热量Q˙conv用于表面液态蒸发和冰晶融化

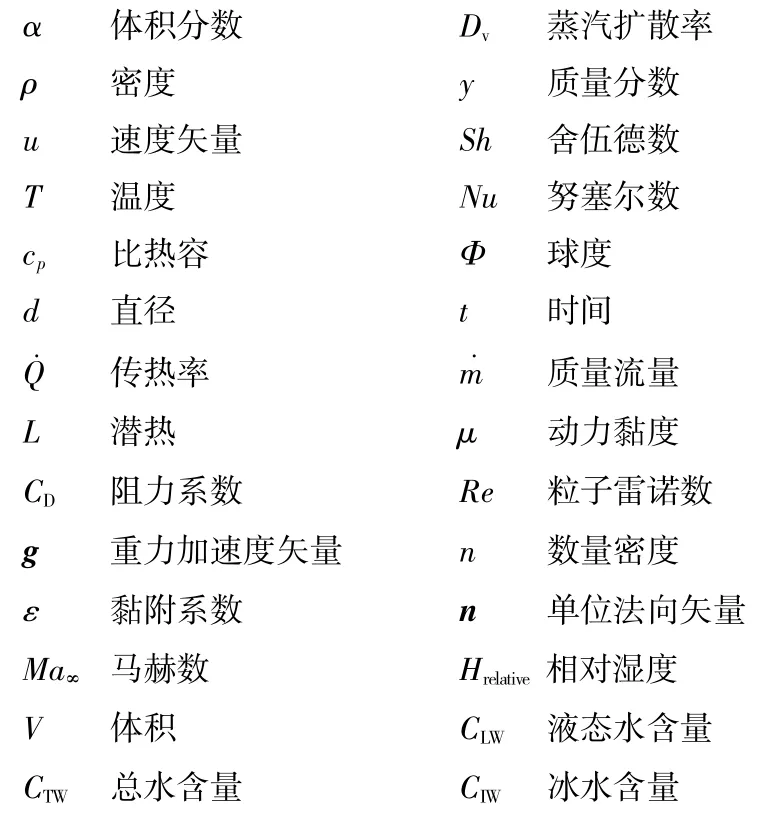
因此,通过混合相粒子能量守恒(式(5))可以推导出冰晶融化率[11]
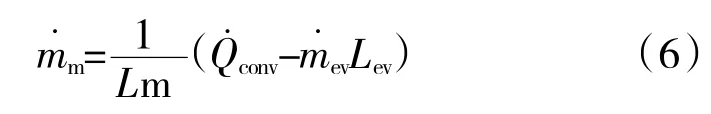
冰晶固态相质量损失主要由融化造成
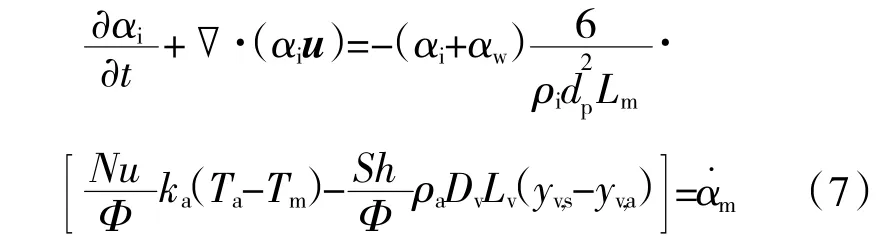
冰晶液态相损失,除了新增融化质量外(等号右边第1 项),还有由于表面蒸发造成的质量损失(等号右边第2 项)
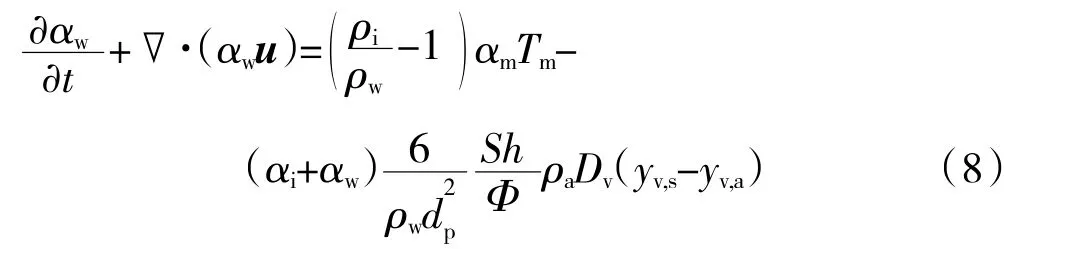
能量方程为
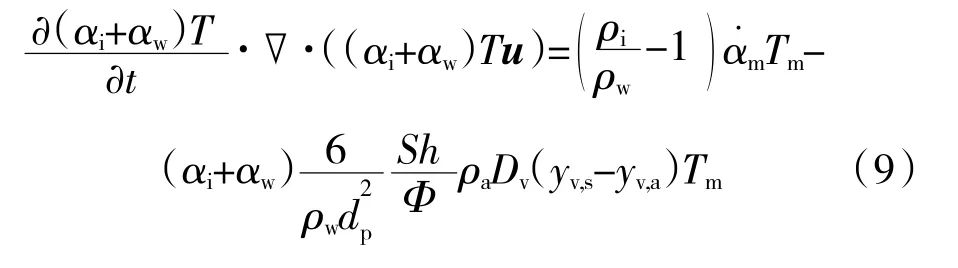
当T>Tm时αi=0,冰晶粒子完全融化成水,质量αi=0 损失主要由蒸发造成

而对流换热和蒸发引起的能量变化为


上述质量、动量和能量方程中需要求解未知变量为α、u 和T,但无法确定粒子直径dp变化。由于粒子数量密度是不变的,因此可以通过粒子数量密度守恒来反映dp变化
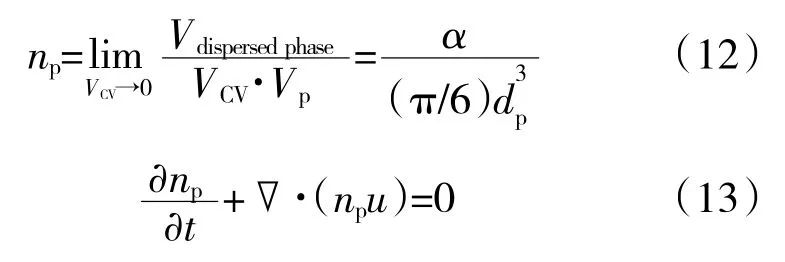
上述控制方程可通过流线迎风伽辽金有限元方法进行求解[15]。
1.2 冰形生长模型
本文冰形生长模型采用经典Messinger 模型,该模型以控制体积建立质量和能量守恒方程[11]。进入控制体积的质量主要是冰晶融化部分、过冷液滴前一个控制体流入质量,而离开控制体积的质量主要是液膜蒸发,结冰、下一个控制体积流出质量(如图1 所示)。因此控制体积的质量方程为

冰层质量守恒方程为


图1 Messinger 模型
控制体积能量守恒方程为
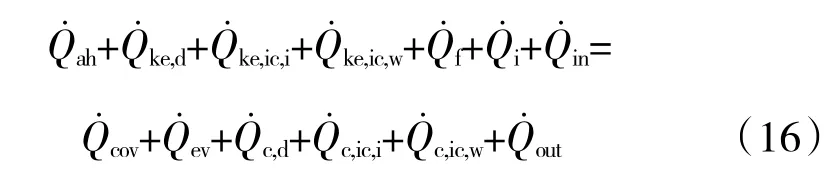
当进入控制体积的液态水质量小于结冰质量m˙f时,即,说明冰晶和过冷液滴在表面立刻结冰,形成霜冰。此时,在控制体内不存在液膜,液态水不会进入下一个控制体积(),同时也没有由于蒸发造成的质量(),冰层升华造成的能量损失将取代式(16)的蒸发能量损失于是冰层质量守恒方程和能量方程为
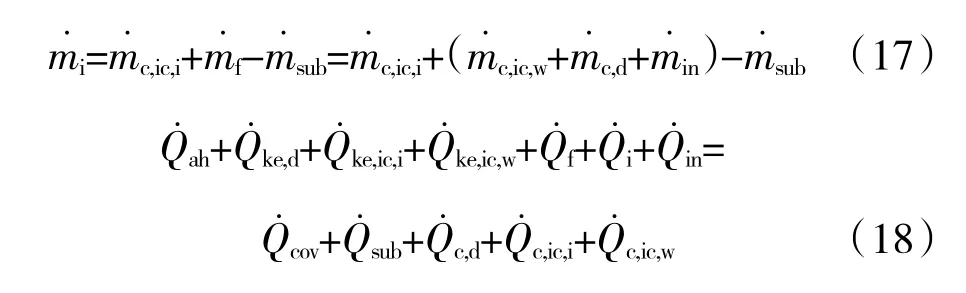


2 算例分析
本文以NRC试验[5,16]中的对称楔形翼型作为研究对象,该翼型前部夹角为40°,后部夹角为20°,弦长220.92 mm(如图2(a)所示)。该试验设备可产生液滴直径=40 μm,冰晶直径=100~200 μm,在本文计算中冰晶尺寸取其中间值,即150 μm。整个流场计算模型(154064 个六面体)如图2(b)所示。进口距翼型前缘约1.27 m,由于该距离过短,同时受试验条件的限制,无法完全模拟来流在压气机中逐渐增温增压过程,纯冰晶在该距离短时间内无法形成混合相。为了模拟压气机工作环境下所形成的混合相,NRC 在试验过程中补充了40 μm 液滴。

图2 对称楔形翼型实物[16]与网格模型
2.1 对比验证
为了验证本文数值方法的准确性,首先以NASA-NRC 风洞试验[16]中的第139 号试验工况(见表1)作对比。

表1 NASA-NRC 第139 号试验工况[16]
本文采用上述数值方法计算后,得到了丰富的流场数据(如图3 所示),通过对比可见,数值结果与试验结果基本相同,但二者存在一定偏差,这是由于本文未考虑风洞壁面效应,出口采用压力远场所致。
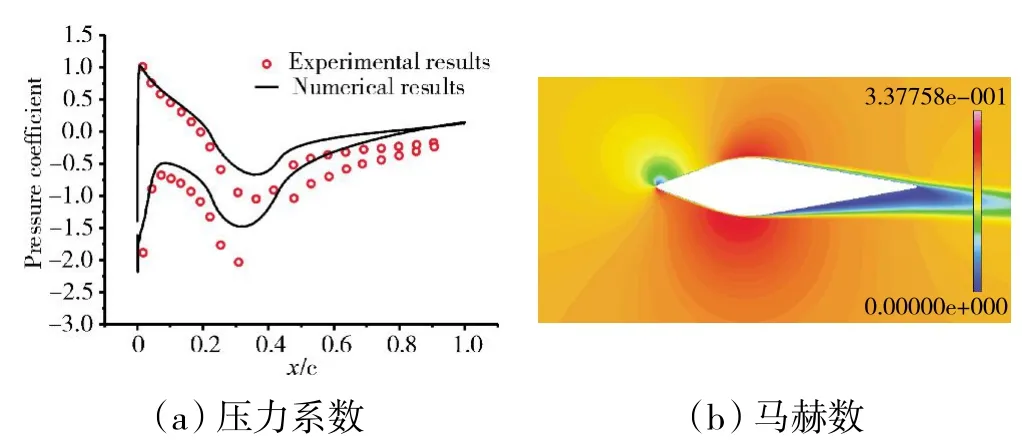
图3 流场结果
粒子轨迹计算结果如图4 所示。从图中可见,尽管计算工况中总温为12.5 ℃,但湿球温度为负值,蒸发过程比较强烈,将吸收大量热量,导致液滴温度逐渐降低,驻点处液滴温度由最初的10 ℃降低至-8℃左右,最终形成结冰条件。而在蒸发过程中,撞击驻点处的液滴在较为强烈的蒸发作用下,其直径由初始的40 μm 变为39.3 μm。在该工况下暴露402 s 后,计算结果与试验结果较为一致,但由于采用单步计算,二者尚存在一定差异,如图5 所示。
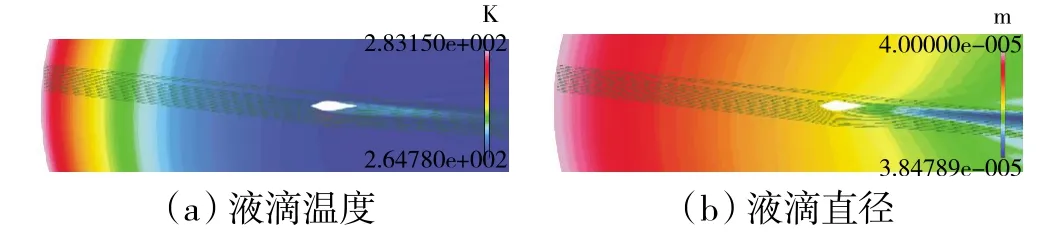
图4 轨迹计算结果

图5 NASA-NRC 的第139 号试验结果对比
2.2 压力对结冰影响分析
为了研究总压对结冰的影响,进行如下工况的计算(表1 中Model A 工况实际为NASA-NRC 试验的第543 号 试验工 况[16],由于公开文献仅提供定性结论,没有太多定量结论,本文没有进行试验数据对比),所有模型计算攻角为0°,冰晶尺寸为150 μm,液滴尺寸为40 μm,结冰时间均为60 s。
翼型表面流场中粒子(液滴和冰晶)直径对比如图6 所示。从中可见,Model A 中翼型表面的液滴和冰晶的直径明显要小于其他2 个模型的。在相同工况下,总压降低会导致蒸发速率增大和湿球温度进一步降低,因此,受蒸发速率影响,在低压环境下(Model A)无论冰晶还是液滴,其质量损失最大。

表2 计算工况I kPa

图6 翼型表面流场中粒子直径对比
翼型表面粒子收集速率和冰层厚度结果对比如图7 所示。从图中可见,液滴/冰晶最有可能撞击翼型前缘(z=±2 mm)位置,在前缘位置3 种工况粒子收集情况相差不大(图7(a))。但在翼型迎风面其他部位,在低压环境下(Model A),粒子收集速率高于高压环境(Model B 和Model C)下的,这是因为粒子尺寸越大,撞击表面后发生反弹或破碎的概率越高,造成表面收集质量速率下降。而从冰层厚度对比结果中(图7(b))可见压力造成的结冰情况差异较大,在低压环境下更容易结冰(Model A 中驻点冰层厚度为4.6 mm,而试验数据为4.5 mm,数值结果与试验结果基本一致)。一方面,低压环境(Model A)表面质量收集速率要高(图7(a));另一方面,低压环境湿球温度更低(Model A/B/C 的湿球温度分别为-3、-1 和1℃),更利于冰层生长。

图7 翼型表面质量收集速率和冰层厚度
综上所述,压力越低,湿球温度越低,蒸发作用越强烈,越容易形成结冰条件,这也解释了为什么发动机内部结冰通常发生在高空环境。
2.3 CLWC/CTWC比例对结冰影响分析
本文还进行工况Ⅱ(见表3)的计算。湿球温度Twb=-3℃,攻角为0°,冰晶尺寸DMM=150 μm,液滴尺寸DMV=40 μm,总含 水 量CTW=4 g/m3(CTW=CIW+ CLW),结冰时间均为120 s。
翼型表面结冰对比如图8 所示,翼型表面液膜厚度如图9 所示,翼型表面液膜速度如图10 所示。从图中可见,Model D 不含液态水(CLW=0 g/m3),冰晶也未形成冰水混合相,干燥翼型表面将无法黏附冰晶形成冰层;Model E 中液态水含量较少,仅仅在迎风面形成液膜(图9、10),冰层也仅仅出现在迎风面;随着液滴水含量增加,翼型表面的液膜开始流向背风面,并在背风面形成冰层(Model F、Model G 和Model H)。此外,从驻点处冰层厚度对比可见(图8),当液滴水占据总含水量一半时(CLW/CTW=0.5)冰层最厚;液态水较少时,液膜厚度较薄,吸附冰晶能力较弱;而冰晶较少时,且液态水较多时,虽然液膜较厚,同样不利于结冰(图9)。

表3 计算工况Ⅱ g/m3
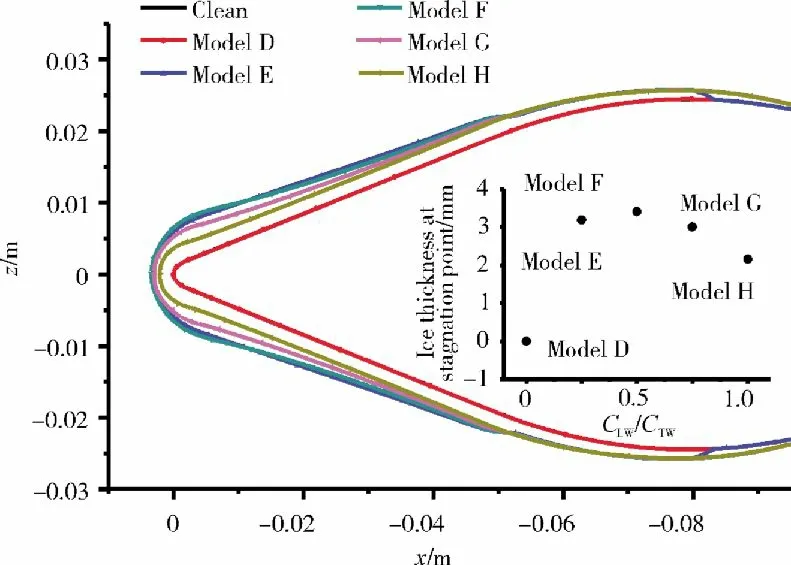
图8 翼型表面结冰

图9 翼型表面液膜厚度
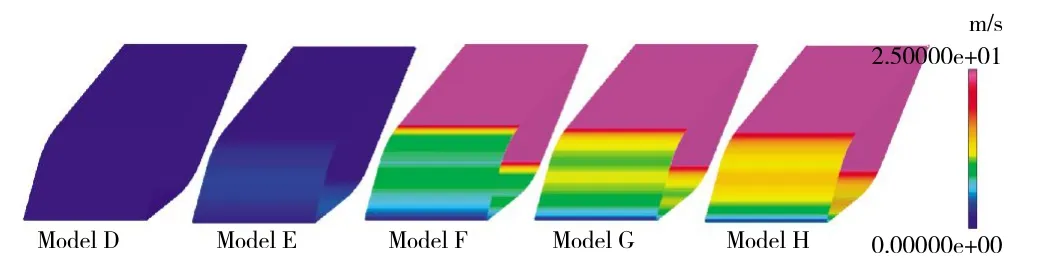
图10 翼型表面液膜流动速度
3 结束语
本文采用数值方法研究了对称楔形翼型冰晶结冰问题。由于NASA-NRC 仅公开极为有限的定量试验结果,大多为定性试验结果,因此本文采用部分定量试验结果对数值方法进行了部分验证,同时进行了压力、CLWC/CTWC对结冰影响的机理分析,计算结果与试验定性结果基本相符。本文方法可为后续发动机结冰机理研究或防冰系统设计提供一定参考。
