学力视域下小学生数学问题意识的缺失及对策

季仕健

（江苏省建湖县实验小学东校区）

学力为通过后天学习与实践获得的态度、能力与知识的集合。学力的养成包括积极态度的培养，学习能力、理解能力、提出问题和解决问题能力、社会适应能力的提高，以及知识的积累等。《义务教育数学课程标准（2011年版）》在原来《义务教育数学课程标准（实验稿）》“培养学生分析和解决问题能力”的基础上,进一步提出要“培养学生发现和提出问题”的目标。学力视域下的小学数学课堂，教学流程设计要以问题为视角，教学活动设计要以问题为载体，注重学生的问题意识的培养。基于这些理论，我分析了当前数学课堂上问题缺失的原因，探究了培养学生问题意识的价值及策略。

一、问题意识缺失的原因

问题意识是批判性思维的前状态。问题意识淡薄将会影响学生学力的提升。影响学生问题意识的原因有以下三方面。

（一）师生对话意识的缺失

没有对话的课堂，学生问题少、不爱问、不敢问、不会问，或问得压抑、犹豫、缺乏自信，最终导致学生“没有问题”。“没有问题”的背后折射出的是学生思考力不强，思维活动不积极。冷静审视我们日常的数学课堂教学，很多教师的教学活动成了演绎教案和知识传授的过程，他们忽略了“引导学生根据具体情境、个体情感需求来提出自己的困惑或疑问”这一重要环节。

（二）提出问题技能的缺智

部分学生过于相信教材、相信权威，习惯于教师提出问题，自己来回答。这导致他们在遇到困惑和疑问时，想问又不知该怎么问，提的问题要么与教学内容联系不紧密，要么与自己的思维不吻合，词不达意，缺乏一定的思维方法与语言表达能力。究其原因，一方面是学生对事物缺少深层次的认识，另一方面是教师的教学只停留在表面，不能引导学生形成深刻的思维。

（三）评价激励重心的失衡

对学生学业的评价，无论是形成性评价，还是终结性评价，很多教师过分注重对学生知识与技能的考查，而较少涉及对学生隐性目标因素（问题意识）的评价，最终导致“学生考什么，教师教什么，教师教什么，学生考什么”这样的失衡现象发生。

二、培养问题意识的价值探寻

数学教师要深刻认识到问题意识是学生学习数学的一种能力，并在教学实践中努力实现，从而使数学教学回归其教育的本义。

（一）指向创新意识和创新能力的培养

《义务教育数学课程标准（2011年版）》指出：“学生自己发现问题和提出问题是创新的基础”，并强调“培养学生的问题意识是培养学生创新意识的好办法。”没有强烈的问题意识，就很难有学生认知的冲动和思维的活跃，更很难培养学生的创造性思维。而在科技突飞猛进的“人工智能”时代，培养学生的创新意识具有战略意义。因此，我们要深刻地认识到问题意识对于创新的价值，更要认识到问题意识对于新时期培养合格的人才的价值。

（二）促进数学思维和学习兴趣的发展

在提出问题的过程中，教师引导学生用数学的眼光观察世界吵。当学生发现书本知识来源于生活，又服务于生活时，其数学思考力就能得到提升；随着思考的深入，学生还会发现，数学学习中新知与旧知是有联系的，新知的学习需要建立在旧知的基础之上。在分析问题的过程中，学生经常开展观察、比较、分析、猜测、推理等数学活动，其倾听、表达、想象和合作能力能得到充分的发展。

（三）显现生本课堂和顺学而导的理念

课堂上，学生围绕具体情境主动提出自己感兴趣的、疑惑的或想要研究的问题时，教师要借助学生提出的这些问题生成为学习内容，进而展开教学。同时，这些问题还需要让学生自己深入探究。在这样的教学中，学生能学会勤于观察、善于发问、精于反思；在这样的教学中，学生会主动参与、兴趣高涨；在这样的教学中，会效果良好、学力提升；在这样的教学中，会有“顺学而导”的意蕴，会有“以生为本”的意旨。

三、培养问题意识的实践路径

华东师范大学孔企平教授指出：“提出问题对于学生的数学学习而言，是一个关键的学习要素,也是一个重要的学习过程。”培养学生的问题意识，提升学生的学力，需要从以下四个方面入手。

（一）营造学生敢提问的宽松氛围

心理学研究表明，良好的课堂氛围是学生善于发现和提出问题的“孕育场”，是学生课堂上自由发问的“情境场”。营造自然、宽松、和谐、充满人文关怀的课堂教学氛围，学生会大胆提问，能勇于发表自己的想法、见解与观点。其中，即使学生提出的问题价值不大，教师也要适当引导，允许重说、改正、补充或寻求帮助，教师对学生真诚的包容，将会保护学生的自信心、自尊心、好奇心和质疑精神。

教学“加法运算律“一课时，课前，我先向学生介绍了自己喜欢的一个体育项目，并适当介绍了这一体育项目的比赛规则，同时让学生介绍他们喜欢什么体育项目……师生间简短而真诚的交流一下子拉近了彼此心理之间的距离，使学生紧张的情绪很快放松下来，为深度学习做好了准备。课始，我借助课前谈话内容创设问题情境，让学生列式算出“喜欢跳绳的有多少人？”当学生列出算式28+17=45（人）和17+28=45（人）时，我继续启发：“仔细观察这两道算式，你们有什么想问的吗？”学生的问题“匣子”很快被打开。他们提出了很多问题，如“28+17=45和17+28=45可以写成一个等式吗？”“像这样的等式还有吗？”“这么多的等式可以用一个等式来表示吗？”“这样的规律在数学上有自己的名称吗？”……学生所提出的问题，直指对“加法交换律”本质的探究。这样，学生就经历了提出问题、列式解答，列举具有共同运算现象的算式进行观察、比较，进而猜想、验证，并抽象、概括出加法交换律的过程。在这个过程中，学生学会了探索问题的一般方法，习得了数学推理等学力。

（二）把握学生想提问的最佳时机

引导学生主动提问的环节，最好放在学生有了一定的学习体验之后。在学生对知识的发生、发展有一定经历和认识之后，他们的疑问会更真实、更切合知识的本质，提出的问题就会更有价值。

教学“百分数的认识”一课时，当学生经历了百分数意义的探索后，他们提出了很多问题：“百分数和分数之间有什么联系与区别？”“分数既可以表示分率，也可以表示具体的量，百分数也可以吗？”“分数的分子都是整数，而百分号前面的数为什么可以是整数，也可以是小数？”……教师可以抓住这个机会鼓励学生发问：“会提问的同学必定是会学习的同学，回顾刚才探索百分数意义的过程，你们有什么想问的吗？”在我的鼓励和引导下，学生提出了一个个具有思考价值的问题。当学生提出这些具有思辨价值的问题时，需要让他们的同伴先介入，互相解答释疑。在这样的过程中，学生会感受到百分数的学习是建立在旧知分数学习的基础之上的，对百分数与分数之间联系与区别的认识会更深刻；在这样的过程中，实现了师生、生生之间的平等对话，使学生体验到了学习数学的无穷乐趣。

正如德国学者克林伯格所认为的：“在所有的教学中都进行着广义的对话，不管什么学科的教学，相互作用的对话，都是优秀教学的本质标识。”

（三）用好学生能提问的有效载体

《义务教育数学课程标准（2011年版）》指出，“综合与实践”板块设置的目的在于：“培养学生的问题意识、应用意识和创新意识，积累学生的活动经验，提高学生解决现实问题的能力。”因此，教师可以借助“综合与实践”这个载体，让学生广泛地参与实践，主动地发现问题、提出问题，并借助自己已有的知识经验和生活经验去开展有意义的探究活动，最终实现解决问题、建构知识、提升学力的目的。

教学“简单的周期”（如图1）这一“综合与实践”内容时，我并没有不放心地“搀扶”，而是放手引导学生观察图中的盆花、彩灯和彩旗的排列规律，再引导根据排列规律提出一些数学问题。

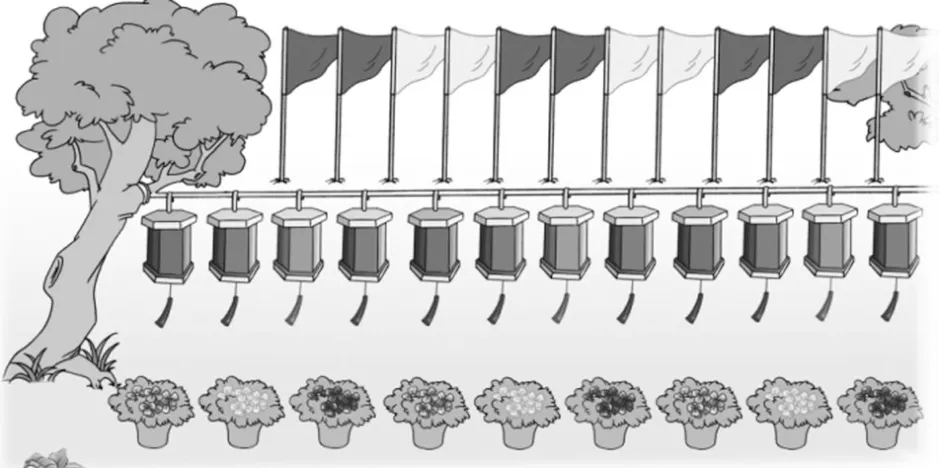
图1

学生用数学思维分析后，提出了问题：“按照盆花、彩灯和彩旗的摆放规律，第100个分别是什么颜色的？”“为什么确定第100盆盆花颜色时是除以2，而确定第100盏彩灯颜色时却除以4呢？”

对于学生的提问，我适时表扬：“抓住问题的关键进行提问的同学是会深度思考的同学，掌声鼓励。”学生在我的鼓励下，提问的意识继续被激发，进而又有学生提出：“确定第100面彩旗的颜色，除以2可以吗？”这个问题是学生自己提出的，我引导学生自己去说理、质疑、辩驳与追问。学生得出了结论：“我们可以把2面红旗看作1组，2面黄旗看作1组，100÷2=50（组），没有余数，所以第100面彩旗是黄旗。”在这个知识的关键处我追问：“真的可以吗，再想一想？”学生的思维快速运转，几分钟后有的学生发现只有总数是4的倍数时，除以2才是正确的。

整节课，学生的提问成为了课堂的主线，问题成为了探究的内容。在提问的过程中，学生的观察力、思考力、思维力得到了发展。关于问题如何解决，我一直退居幕后，让学生群体的智慧产生共振，在关键处、疑难处适时介入。课后，我布置学生用所学的周期规律设计一份美化校园的方案，使学生也得到了一次实践应用的锻炼机会，体现了数学的价值，发展了学生的创造性思维，学生的学习兴趣也更浓厚了。

（四）善待学生预设之外的提问

布卢姆曾说：“人们无法预料教学所产生的成果的全部范围。”可见，课堂上面对一个个鲜活的生命个体，他们对于同样的问题都会有自己独特的思维方式和思考路径，教师再充分的预设，也不会完全穷尽教学中的“生成”。面对预设之外的学生提问，教师首先要真心悦纳，表扬学生善于观察，能发现并提出问题，以保护学生提问的热情。其次，还要合理处置。简单的问题教师可以当场予以回答或说明，太过个性化的问题，教师可采取适当的方法告知，与本节课教学有关、且有探索价值的问题可以带领学生一起研究解决，需要社会实践的问题可以布置学生课后调查、访问，返校后可以安排交流的环节。

教学“连除应用题”一课时，教材上有这样一道习题：

一盒乒乓球有6个，每个乒乓球3元。张老师买乒乓球付了216元，买了多少盒乒乓球？

教学时，我让学生列式解答，然后组织反馈，这道习题的教学就算完成了。但就在这个时候，我发现有几位学生面露疑色。学生有问题，置之不理不是教师的正确选择，要让学生把问题提出来。“老师，我是这样列式的，216÷6÷3=12（盒），虽然结果一样，可216÷6表示什么呢？”我敏锐地意识到，这是一个真问题，是一个好问题，如果让学生思维碰撞一下，他们的收获会更多，课堂也会走向深入。于是，我让学生围绕“能不能这样列式？216÷6表示什么？”展开了充分地讨论。在部分学生觉得可以这样列式，但用语言又难以表达清楚时，有一个学生想到了用画图来直观表征（如图2）。通画画图，学生的思维一下子被打开，真正实现了深度思维。这样，整节课散发出积极、热烈的气氛，生本和谐的课堂得以充分展现，这是培养学生发现问题、提出问题的明智之举。

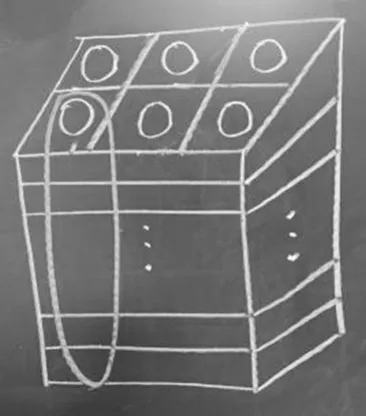
图2

数学教育真正的目的应是让学生不断地提出问题，思考问题。但从培养学生发现问题和提出问题的能力角度来说，有一类问题是缺乏价值的。如在日常的数学教学中，我们经常会看到教师板书课题后就问学生：“看到课题你们有什么想问的？”学生会提出“是什么”“为什么”“有什么用”的问题。其实，这些都是低层次的、“不是问题的问题”。况且，学生提出这些问题时一般都不需要深入思考，只要模式化提问就行了，因为任何一个知识点都存在“是什么”“为什么”“有什么用”的问题。因此，培养学生的问题意识，除了让学生养成敢提问、想提问的习惯之外，还要培养学生能提出真问题、有价值的问题的能力。