一种机器人用新型异步电机定子磁链观测器

曾 欣

（宜宾职业技术学院，四川 宜宾 644003）

1 引言

随着工业的发展，机器人广泛应用于各个领域。在机器人构件上，各转动部分多采用电机作为动力驱动。由于机器人在执行某些特定工作的过程中，会经常使得电机反复启停或者正反转，因此，在实际工业应用上会出现电机位置精度不准、执行动作误差大甚至失效等现象。为此，以某一工业机器人转动臂中的异步电机为研究对象，对其定子磁链观测器算法展开研究，以获得更好的控制效果。

定子磁链观测器是实现异步电机直接转矩控制、高精度无位置传感器矢量控制的重要基础，因此，实现定子磁链的高精度观测具有重要意义。常用的异步电机定子磁链观测方法主要包括电压模型法和电流模型法两种。传统的电压模型定子磁链观测器实现简单，对电机参数的依赖性较小，但是其所使用的纯积分运算易受积分初始值和积分漂移的影响。传统的电流模型定子磁链观测器虽然克服了电压模型法的缺点，但是却需要已知电机的励磁电感等电气参数，从而对参数的依赖性较强。当电机分别在基速以下的恒转矩区和基速以上的恒功率区运行时，由于磁路饱和程度不一致，励磁电感将会发生非线性变化，从而影响定子磁链的观测精度。文献[1-5]分别研究了不同的改进型电压模型定子磁链观测方法。文献[1]提出了三种递进的改进型定子磁链观测方法，相比前两种方法，所提的第三种方法可实现较准确的定子磁链观测。文献[2-3]研究了采用低通滤波器代替积分的改进型电压模型定子磁链观测方法，但是该方法对直流偏量的抑制能力有限。文献[4]研究了采用高通滤波器代替积分的改进型电压模型定子磁链观测方法，但是该方法受电机3次、5次、7次等低次谐波的影响。文献[5]研究了采用带通滤波器代替积分的改进型电压模型定子磁链观测方法。该方法可实现直流偏量和低次谐波的抑制，但是实现较复杂。此外，文献[6-7]研究了混合电压电流模型定子磁链观测方法，以将电压模型法和电流模型法的优点融合在一起。但是，如何克服电机电感参数的影响还有待进一步研究。

近年来，滑模观测器方法因鲁棒性强、实现简单等特点而得到广泛应用，其中，文献[8]研究的极致扭曲滑模算法是滑模理论的一个新进展。将该算法应用到了部分机器人关节电机—异步电机中，以实现异步电机的高精度定子磁链观测，从而为高性能电机控制奠定一定的基础。对比仿真和实验结果验证了该方法的优越性。

2 极致扭曲滑模观测器的建立

在静止α-β坐标系中，异步电机的数学模型可表示为[9]：

式中：is—定子电流；us—定子电压，下标α和β分别表示静止α-β坐标系上的两个分量；ωr—转速；ψrα、ψrβ—转子磁链；p—微分算子；k1、k2、k3、k4的表达式，如式（2）所示。

式中：Rs—定子电阻；Lm—励磁电感；Ls—定子电感；Lr—转子电感；Tr—转子时间常数，满足 Tr=Lr/Rr，Rr—转子电阻；σ—漏

根据文献[10]，可建立极致扭曲滑模观测器，如式（5）所示。其框图，如图1所示。文献[8]基于李雅普诺夫稳定性理论，对这类极致扭曲滑模算法的稳定性给出了严格证明。只要选择合适的δ和λ，就可保证系统收敛，且保证系统对外界扰动具有鲁棒性。

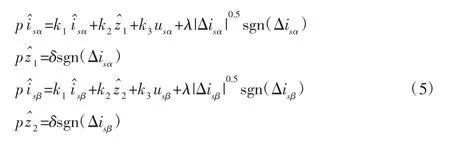
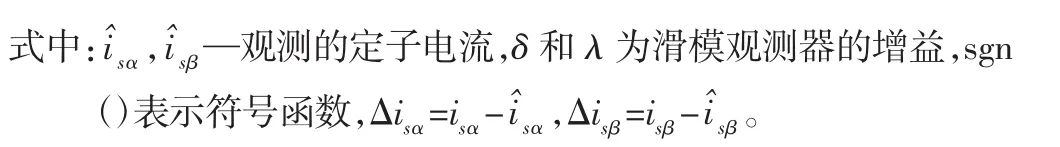
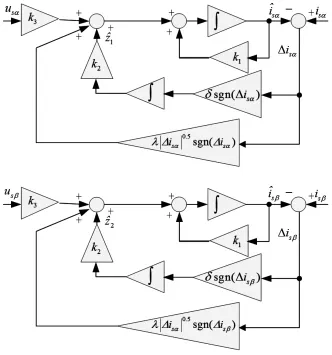
图1 极致扭曲滑模观测器框图Fig.1 Block Diagram of Auper-Twisting Aliding Mode Observer

3 定子磁链和电磁转矩观测方法

如式（5）所示，当所设计的极致扭曲滑模观测器收敛时，可以估计得到中间变量zˆ1、zˆ2，然后根据式（4）可得转子磁链如下：

根据上述方法，通过建立极致扭曲滑模观测器，即可分别估计得到电机的转子磁链、定子磁链和转矩。如果要实现无位置传感器矢量控制，还可以直接根据估计得到的转子磁链估算得到电机的转子位置和转速。如果要实现直接转矩控制，则可以将估计得到的定子磁链和转矩作为反馈，从而实现高精度的转矩调节。

4 混合电压电流模型的定子磁链观测方法

现有的定子磁链观测方法主要包括改进的电压模型磁链观测方法和混合电压电流模型磁链观测的方法。文献[6-7]所研究的混合电压电流模型磁链观测方法可采用电流模型磁链观测器对电压模型进行校正，实现准确的定子磁链观测，因此这类方法得到广泛应用。典型的混合电压电流模型定子磁链观测器结构，如图2所示。由图2可见，该方法同时包含了电压模型磁链观测器方法和电流模型磁链观测器方法。电流模型磁链观测器得到的转子磁链与电压模型磁链观测器得到的转子磁链之差经过比例积分调节器处理，然后用于校正电压模型磁链观测器，从而克服了电压模型中的纯积分问题，实现了定子磁链和转子磁链的观测。然而，由于采用了比例积分调节器，稳态时，基于电压模型的定子磁链观测结果必然与基于电流模型的定子磁链观测结果相同，而电流模型定子磁链观测器受电感参数的影响，从而导致该方法依然受电感参数的影响。

图2 混合电压电流模型定子磁链观测器Fig.2 Stator Flux Observer Combined Voltage Model with Current Model

下面对此进行仿真对比研究。

5 仿真分析

仿真所采用的电机额定电压为220V，额定励磁电流为8A，极对数为2，定子电阻为1.26Ω，转子电阻为0.2Ω，互感为0.05H，漏感为0.0047H。

在MATLAB/SIMULINK里分别实现了所提出的极致扭曲滑模观测器算法和混合电压电流模型算法，并对比研究了基于这两种算法的定子磁链和电磁转矩观测效果。首先研究了基于混合电压电流模型定子磁链观测方法的定子磁链观测结果。仿真时，给定频率为20Hz，给定励磁电流为8A，转矩电流为16A。励磁电感Lm在1.4s时由0.05H逐渐增加为0.1H。仿真结果，如图3所示。由图 3（a）到图3（e）可见，当 Lm增大时，与实际定子磁链相比，估计的定子磁链增大，定子磁链估计误差增大，同时，电磁转矩也增大，这表明基于混合电压电流模型的定子磁链观测方法受Lm的影响较严重。在励磁电感发生变化时，估计的定子磁链和转矩均发生了明显改变，精度大大降低。而在电机实际运行中，电感Lm在电机不同的运行条件下必然会发生改变，这就导致常规基于混合电压电流模型的定转子磁链观测器方法不能很好的适用于复杂运行工况下的异步电机，特别是在经常停机、启动、正反转的机器人应用场合。

在Lm变化时基于所提出的极致扭曲滑模算法的定子磁链和电磁转矩观测结果，如图4所示。图4仿真条件与图3一致，励磁电感Lm在1.4s时由0.05H逐渐增加为0.1H。对比图3、图4可以发现，所提算法估计得到的定子磁链和电磁转矩受励磁电感的影响很小，表明了该算法对励磁电感参数的鲁棒性。

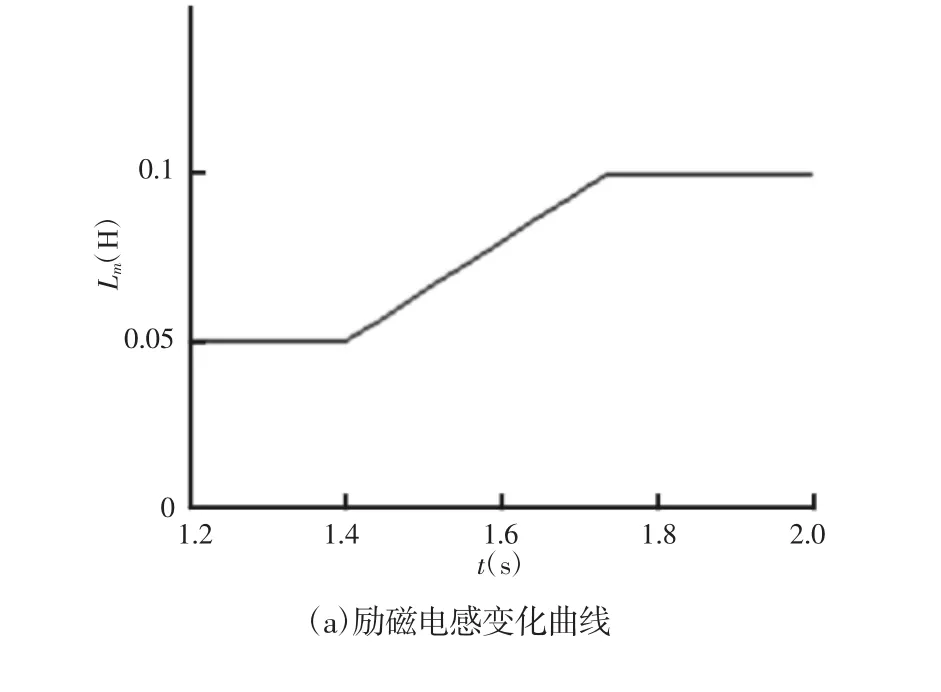
图3 Lm增大时基于混合电压电流模型的定子磁链和电磁转矩观测仿真结果Fig.3 Simuliation Results of the Atator Flux and Electromagnetic Torque Based on the Hybrid Observer when LmIncreased

同时，由于算法需要引入多次参数运算，参数运算的舍入误差导致在励磁电感准确时，定子磁链和电磁转矩也存在微小误差，但是由于误差很小，也可以忽略不计。实际系统中，观测器使用的励磁电感值与真实的励磁电感不可能完全相同，而所提算法在励磁电感在较大范围内变化时，都能保证观测的定子磁链和电磁转矩具有较高的精度，从而为实现异步电机的高精度直接转矩控制和无位置传感器控制奠定基础。

图4 Lm增大时基于所提方法的定子磁链和电磁转矩观测仿真结果Fig.4 Simuliation Results of the Atator Flux and Electromagnetic Torque Based on the Proposed Method when LmIncreased

6 实验研究

为了进一步验证所提方法的有效性，进一步建立了实验平台，并进行了实验研究。实验所用电机参数与仿真一致。实验平台，如图5所示。给出了励磁电流为8A，电机运行频率为5Hz时的采用所提方法的实验结果，如图6所示。Lm在由0.05H逐渐增加为0.1H时的定子磁链观测实验结果，如图6（a）所示。Lm在由0.05H逐渐增加为0.1H时的电磁转矩观测实验结果，如图6（b）所示。

图5 实验平台照片Fig.5 Photo of the Experimental Platform

图6 Lm增大时定子磁链和电磁转矩观测实验结果Fig.6 Experimental Results of the Atator Flux and Electromagnetic Torque When LmIncreased

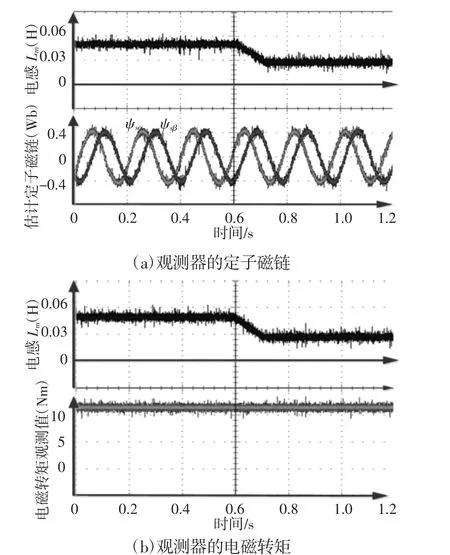
图7 Lm减小时定子磁链和电磁转矩观测实验结果Fig.7 Experimental Results of the Atator Flux and Electromagnetic Torque When LmDecreased

由图6可见，在Lm增大时，采用所提方法观测得到的定子磁链和转矩不受影响，这与仿真结果一致。

同样实验条件下，Lm在由0.05H逐渐减小为0.025H时的定子磁链和电磁转矩观测实验结果，如图7所示。由图7同样可见，所提方法对Lm变化具有较强的鲁棒性，这进一步验证了所提方法的有效性。

7 结语

提出了一种基于极致扭曲滑模的新型异步电机定子磁链观测方法，并与传统的混合电压电流模型定子磁链观测器进行了对比研究。仿真和实验结果均结果表明，所提出的定子磁链观测方法有效克服了电机电感参数的影响，从而提高了定子磁链和电磁转矩的观测精度，可为异步电机的高精度直接转矩控制和高精度无位置传感器控制奠定基础。