考虑不确定性的车身在线装配精度的优化控制研究

郭允明，张恃铭

（上海理工大学机械工程学院，上海 200093）

1 引言

为了满足日益提升的用户需求，机械类产品的结构设计越来越复杂，其制造、装配的难度也随之增大，特别是轿车车身由众多零部件、经过上百个工位加工装配而成，致使在车身装配过程不仅复杂而且还充斥着众多不确定性因素，如来料、工艺以及测量等因素导致的不确定性影响等，因此如何在不确定性下对车身装配质量的在线工艺控制研究具有重要意义。

传统的制造质量控制方法主要基于统计数据分析的监控、诊断等事后控制模式，如文献[1]中对统计过程控制（SPC）和工程过程控制（EPC）的集成使用进行了研究解决制造过程波动预警问题。文献[2]运用SPC与EPC集成监控原理对制造质量过程状态进行监控，然后对制造过程进行调整。文献[3]运用SPC监控原理对车门尺寸偏差数据进行过程状态监控。根据质量监控表现。文献[4]基于调度算法提出面向装配过程扰动的动态调度算法，实现装配过程的可视化监控。文献[5]分别提出基于状态空间模型的故障诊断，以及Ceglarek等提出的基于多元统计分析与工艺知识结合的质量诊断方法。但此类在制造过程中的进行监控、诊断的方法，只能在问题发生以后对制造过程进行控制、调整，在此过程中已经产生了废品，造成了不必要的损失。

智能制造模式下，机器视觉、线旁在线测量、机器人等自动化技术、大数据技术的发展使得装配制造质量控制技术发生重大改变[6]，即逐渐转化为在线装配下的过程质量优化控制模式。文献[7]2013年首次提出了复杂制造系统中的过程质量改进（IPQI）数据融合的概念，与传统的质量控制概念不同，IPQI注重工程领域知识与过程中传感数据的集成，实现在线过程监控、诊断（而不是离线数据分析）、预防缺陷（而不是检测缺陷）并进行在线自动补偿控制（而不是离线调整）。该质量优化控制模式最初在机加工过程得到应用，如文献[8]研究数控机床加工过程在线监测及加工误差分析与补偿方法的问题，基于分析结果，通过软件实时补偿原理，结合数控机床控制系统特点，对主要误差源进行在线补偿，从而达到提高加工精度的目的。文献[9]结合历史数据和在线数据，提出基于偏最小二乘（PLS）的非线性模型预测控制（MPC）方法，以适应大规模制造过程的特点。文献[10]基于Kriging模型，提出了一种全局多目标优化算法用于将优化过程与实验过程相结合文献[11]提出一种基于代理模型的复合材料零件装配过程中尺寸变化的最优前馈控制策略，并使用Kriging代理模型[12-13]进行尺寸预测，然后将该模型嵌入到最优前馈控制算法中进行多目标优化。

在Kriging建模理论方面，文献[14-15]将应用于确定性计算机实验的设计与分析Kriging理论，扩展到含有随机不确定性的仿真环境，描述了随机模拟中固有的内在不确定性和未知的外在不确定性。文献[16]针对不确定性问题采用三阶段序贯试验设计方法使随机Kriging代理模型精度得到提高。文献[17]采用随机Kriging代理模型方法对柔性机翼气动外形进行优化设计。相比确定性优化设计，采用随机Kriging代理模型优化设计能够考虑设计变量和参数的扰动，保持设计结果在不确定性影响下的性能稳定。

目前对于制造过程质量优化控制存在以下特点：（1）制造过程偏差因素多、精确地关联关系建模困难；（2）在实际建模过程中，模型的某些输入变量或参数存在不确定性[18]，如某些制造工艺参数、零部件的材料参数不确定、测量系统不确定性等；（3）在线的装配工艺控制要求的实时性，即需要在快节凑生产模式下实施工艺参数的优化控制，及时预防缺陷；上述问题导致现有基于确定性机理模型的工艺参数优化控制方案难以满足实际需求，为此这里提出考虑工艺不确定性的车身在线装配工艺的优化控制方法，并将其应用于车门装配的工程案例中进行验证。

2 基于随机Kriging的车身装配精度建模

2.1 车身在线装配工艺控制工位简述

车身装配线主要包括在线测量设备（机器视觉）、车身薄板件装配工位（零部件、工装夹具、焊装机器人等）、工艺参数控制单元等部分，如图1所示。

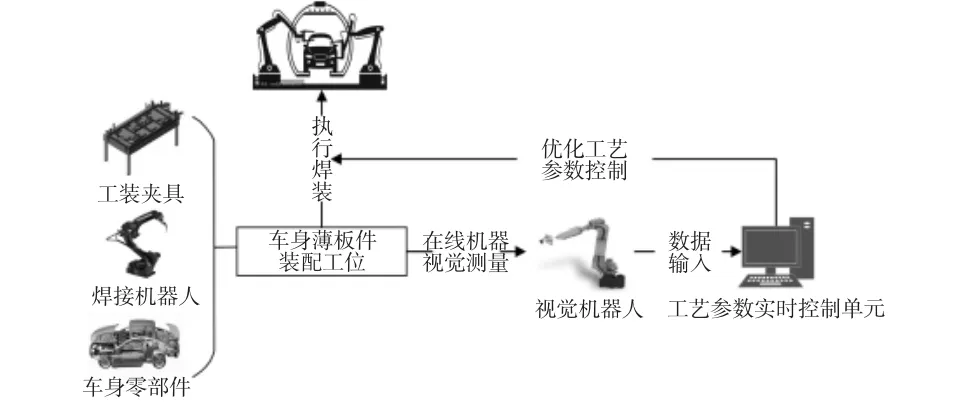
图1 车身在线装配工艺控制过程示意图Fig.1 Body Online Process Control Station Map

2.2 装配工艺的随机Kriging建模

薄板件装配偏差模型主要有基于运动学的刚性模型和基于有限元的柔性模型等。刚性模型主要考虑工装、零部件的运动学位姿模拟装配体累积偏差；柔性模型精度较刚性有所提高，但受到热、力等多场耦合以及柔性变形非线性，且现有基于有限元模型的多工位偏差传递建模效率不高。模型主要用于工艺方案的验证与改进设计等。由于受到制造过程的动态性、不确定性等因素影响，上述机理模型难以应用到制造工艺参数的实时控制中。

代理模型，通常是指在分析和优化设计过程中替代那些比较复杂且费时的数值分析的近似数学模型，也称为响应面模型或元模型。在现有的代理模型方法之中，Kriging模型由于其对非线性函数的良好近似能力和独特的误差估计功能，正受到越来越多研究者的关注，是目前最具代表性和最具有应用潜力的代理模型方法之一[12]。在此基础上，随机Kriging模型是将应用于确定性的计算机实验设计和分析的Kriging理论推广到包含外部随机不确定性的仿真实验中去。

一般代理模型的构建包括确定实验方案、计算参数、构建模型、评价模型精度等步骤。这里中基于随机Kriging代理模型的车身装配偏差模型构建流程，如图2所示。

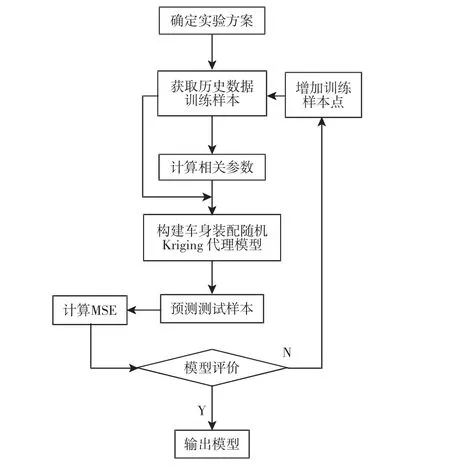
图2 车身车门装配偏差随机Kriging模型流程图Fig.2 Stochastic Kriging Model Flowchart of Body Door Assembly随机Kriging代理模型，如式（1）所示。

式中：x=［x1，x2，…，xn］—输入变量矩阵，表示工装定位、焊接、来料零部件等工艺输入变量；Yj（x）—关于x的第j个响应值，指该工位装配体关键检测特征；FT（x）—关于x的回归函数表示x=［x1，x2，…，xn］与Yj（x）的关系；β—回归函数中的未知回归系数向量，β采用极大似然估计得到；M（x）—均值为0的平稳高斯随机过程的实现；M（x）—从函数空间中随机抽样的，假设该空间中的函数具有空间相关性，这意味着，如果 x 和 x′在空间上很接近，M（x）和 M（x′）的值会趋于相似，将M（x）的随机性称为外部不确定性，（如在输入某些变量时出现重大差错），所以它是强加于问题上并不是其固有的，用来帮助建立随机代理模型；εj（x）是在x处的重复样本波动，其均值为0，方差为η（x），表示随机仿真中内部固有的不确定性，在装配工艺中，指代某个检测特征，由于输入变量的内部误差，导致多次装配结果出现波动。并且假设它与其他重复样本的固有和非固有不确定性M（x）之间相互独立。

对于内部固有的不确定性的方差η（x）的求解，将输入变量分为多组（ni，xi，Yj（xi）），其中xi，为第i组输入变量，ni为在xi处重复样本的数量，Yj（x）是关于x的第j个响应值所以设样本均值为：

计算预测点的预测数据与原始数据之间的平均离差平方和的，越接近0说明模型拟合的越好。该均方差可用于指导加入新样本点，以提高代理模型精度或逼近优化问题的最优解。

3 装配质量的在线优化控制策略

在装配过程中，装配体大都是由多个零部件在多个装配工位被依次装配而成，在此过程中，零件和装配体之间总是存在着的尺寸偏差，这些尺寸偏差对最终产品的质量、可靠性、功能和成本都有重要的影响，因此，在零件装配过程中在线对工艺优化和质量控制，降低尺寸偏差是一项重要而又具有挑战性的任务。这里中基于随机Kriging的制造质量在线优化控制流程，如图3所示。

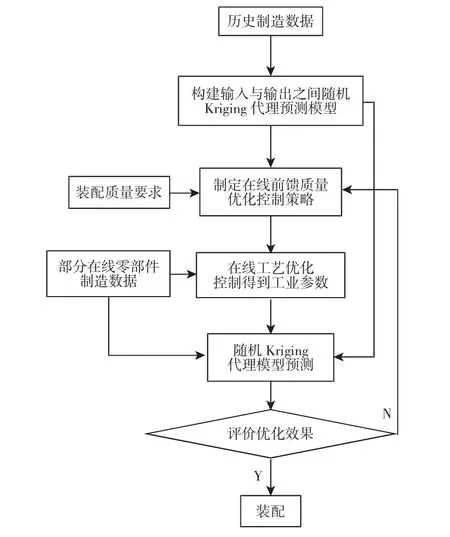
图3 基于随机Kriging的制造质量在线控制流程图Fig.3 Based on Random Kriging Online Control Flowchart for Manufacturing Quality

以下将结合图3对装配工艺的在线优化控制方法介绍。在整个装配过程中，工艺输入输出参数分别表示为：

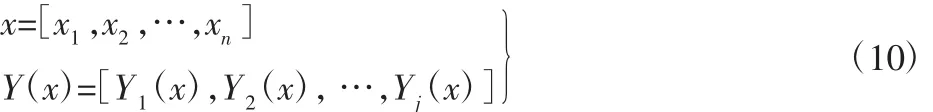
式中：xi—第i个工艺环节的制造偏差或工艺参数；Yj（x）—x所对应的第j个装配质量表现，假设装配过程已经在线测得了［x1，x2，…，xi］制造偏差数据，而第i+1个工艺参数［xi+1，xi+2，…，xi+k］为待优化控制参数，根据装配工艺的在线优化控制方法，先利用整个装配过程的历史数据，建立输入与输出之间的关系模型（如式（1）随机Kriging代理模型），然后基于输入与输出的关系模型设置多个目标函数与约束函数建立优化模型，其形式，如式（11）所示。

式中：U（x）—目标函数集合；V（x）—约束函数集合（本次车身装配工艺优化模型的具体目标与约束函数将结合制造质量要求，将在下文中列出）。

然后利用优化程序将在线数据结合式（11）进行工艺参数优化得到装配工位的工艺参数的优化值［xi+1，xi+2，…，xi+k］。最后将［x1，x2，…，xi，xi+1，xi+2，…，xi+k］输入到所建立的输入输出关系模型中，检验优化后装配质量表现，若满足则装配系统的执行装置按优化结果执行，通过在线调整工艺参数控制该装配工位的焊装质量，在装配工装、在线视觉、工艺参数控制单元、工装与焊接机器人执行装置构成的工艺系统中实现焊装工艺的实时、优化控制，保证薄板件装配质量。

4 车门装配案例分析

4.1 案例描述

将结合某车型的后车门装配案例进行分析，该车型的后车门装配总成由车身侧围、上、下铰链及其相应螺栓和后车门总成组成，该装配案例包含三个装配工位，在第一个工位中上下铰链用工装装配至车身B柱并用螺栓固定；在第二个工位中，车门装配至铰链上并用螺栓打紧；在第三个工位中，打紧所有螺栓。铰链和后车门总成结构图，如图4所示。

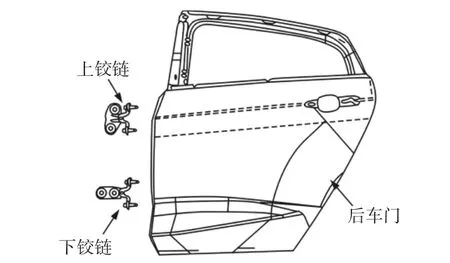
图4 铰链和后车门总成结构图Fig.4 Hinge and Rear Door Assembly Structure Diagram

装配完成后为评价装配质量的5个测量位置，其测量特征为均为间隙（Gap1、Gap2、Gap3、Gap4、Gap5）（单位/mm），如图 5所示。

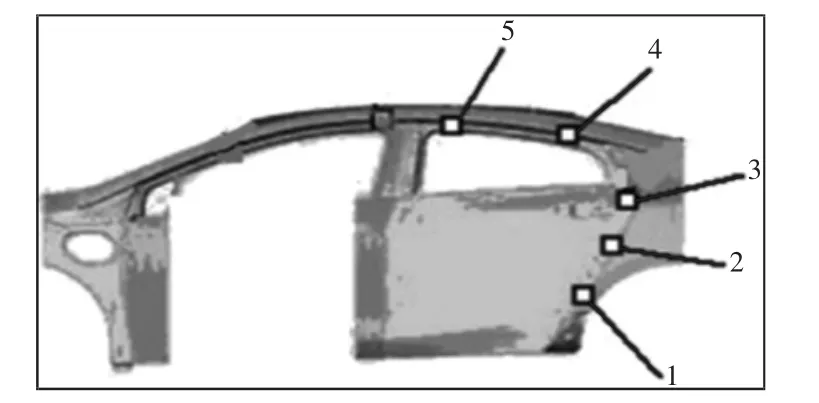
图5 左后车门测量特征Fig.5 Measurement Features of the Rear Left Door

已知对Gap1，Gap2，Gap3有影响的输入变量有各间隙对应的车身测点x1，车门测点x2，车门侧面孔1的X向偏差x3，车门侧面孔4的X向偏差x4，车门侧面孔2的X向偏差x5，上铰链X向调整量x6，下铰链X向调整量x7。

对Gap4，Gap5有影响的输入变量有车身测点X1，车门测点X2，车门铰链孔1的Z向偏差X3，车门铰链孔4的Y向偏差X4，上铰链Z向调整量X5，下铰链X向调整量X6。

4.2 建立随机Kriging车门装配模型

（1）分别选取 Gap1，Gap2，Gap3，Gap4，Gap5 各 50 组的历史制造数据；

（2）根据上文中式（3）求出 Gap1，Gap2，Gap3，Gap4，Gap5 各自的随机Kriging模型参数内在不确定性的方差η（x）；

（3）将输入变量，输出变量，及模型所需要的参数，输入到Matlab程序中；

（4）得到车门装配的随机Kriging预测模型。

为了对比分析是否考虑工艺不确定性的模型对预测精度MSE的差异影响，凸显随机Kriging模型的预测优势，这里选取简单回归模型和UniversalKriging模型，与随机Kriging模型的预测精度进行比较，评价随机Kriging模型的预测性能。如图6～图10所示。通过预测20个测试样本，计算三种模型的预测精度指标MSE结果，如表3所示。从表1中数据对比分析，随机Kriging模型的预测性能要优于简单回归模型和Universal Kriging（UKriging）模型。随机Kriging模型的预测精度高于其他两个模型的原因是它充分考虑了仿真实验中的内部固有和外部非固有不确定性因素的影响。

图6 Gap1预测值对比Fig.6 Gap1 Forecast Value Comparison

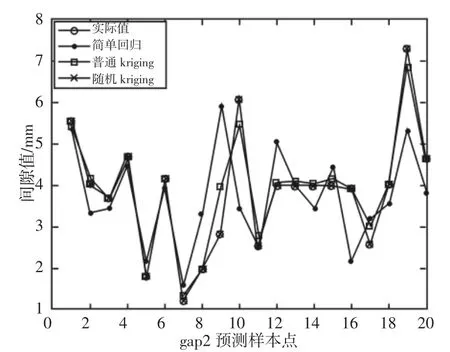
图7 Gap2预测值对比Fig.7 Gap2 Forecast Value Comparison

图8 Gap3预测值对比Fig.8 Gap3 Forecast Value Comparison

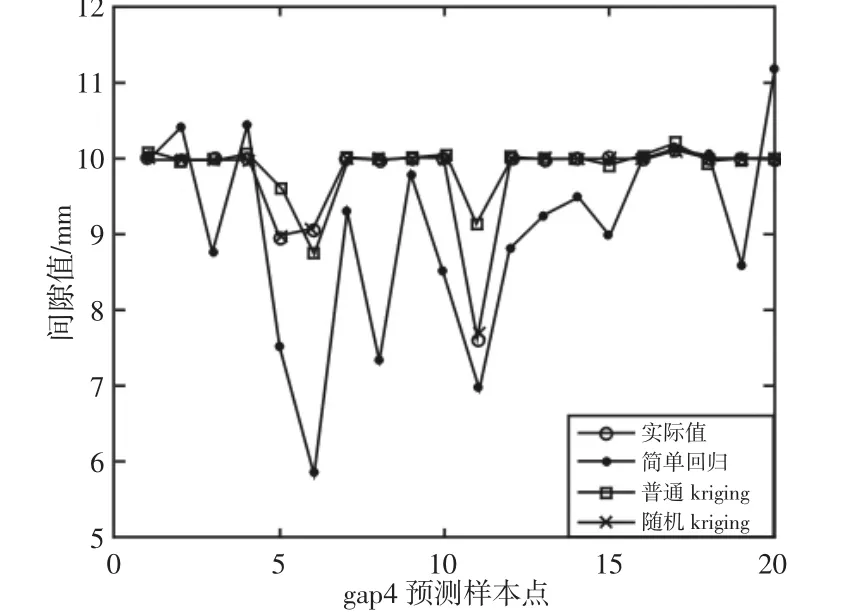
图9 Gap4预测值对比Fig.9 Gap4 Forecast Value Comparison

图10 Gap5预测值对比Fig.10 Gap5 Forecast Value Comparison

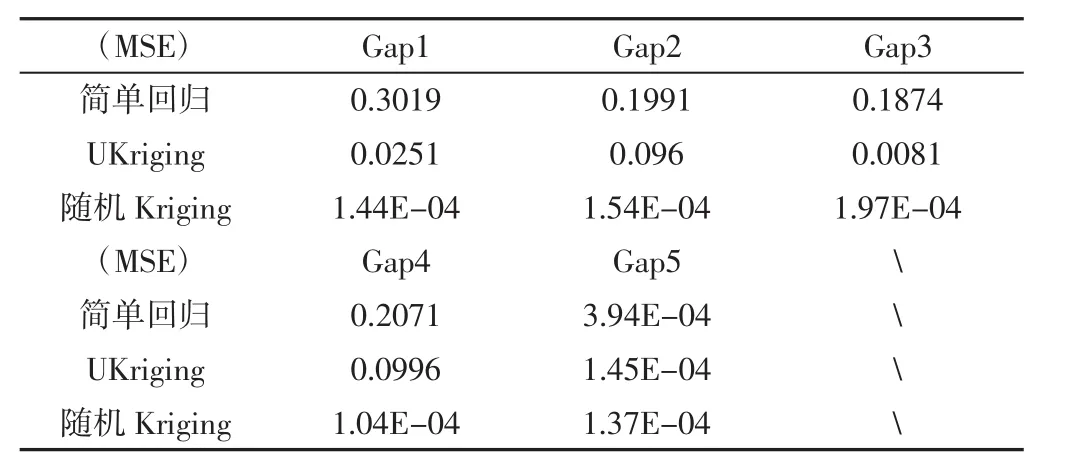
表1 三种模型预测精度对比Tab.1 Comparison of Prediction Accuracy of Three Models

4.3 基于优化控制策略的车门装配工艺在线优化

根据上述的装配质量的在线优化控制方法，对车门装配过程铰链安装位置参数进行在线优化。假设基于在线测量车身、车门零部件的偏差数据已知，如何在工艺可行范围内，在线优化铰链安装位置以保证车身、车门的整车间隙质量的一致性与波动性是本案例的目标。因此，通过配质量的在线优化控制方法利用目标函数和约束函数，对铰链调整量进行量化分析，优化模型为：

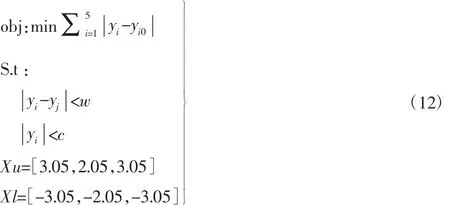
针对5000组车身的装配工艺的优化仿真，对比结果，如图11～图15所示。

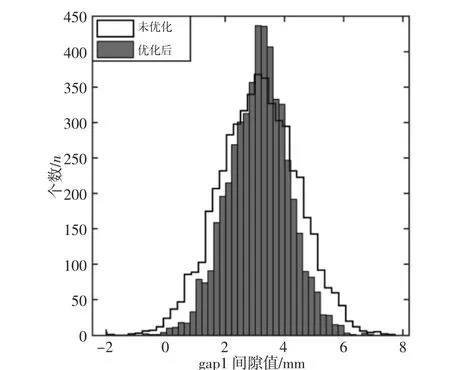
图11 Gap1间隙值优化前后对比Fig.11 Gap1 Comparison Before and After Clearance Value Optimization

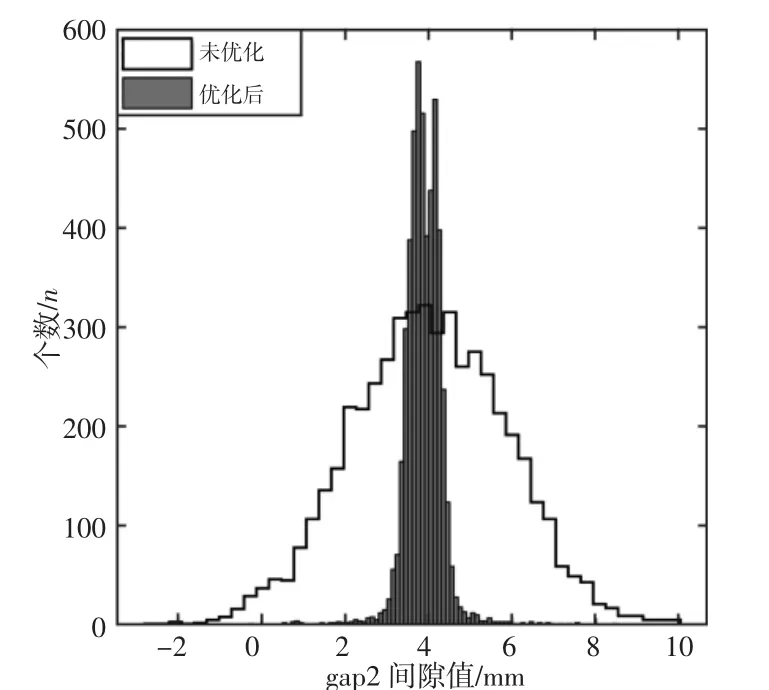
图12 Gap2间隙值优化前后对比Fig.12 Gap2 Comparison Before and After Clearance Value Optimization

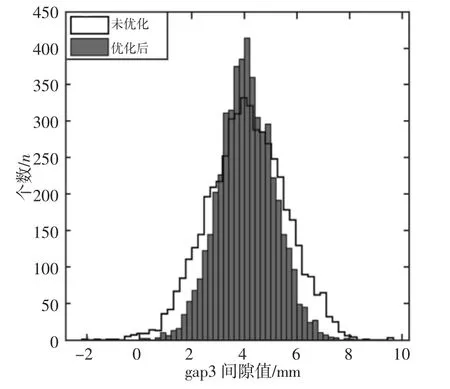
图13 Gap3间隙值优化前后对比Fig.13 Gap3 Comparison Before and After Clearance Value Optimization

图14 Gap4间隙值优化前后对比Fig.14 Gap4 Comparison Before and After Clearance Value Optimization

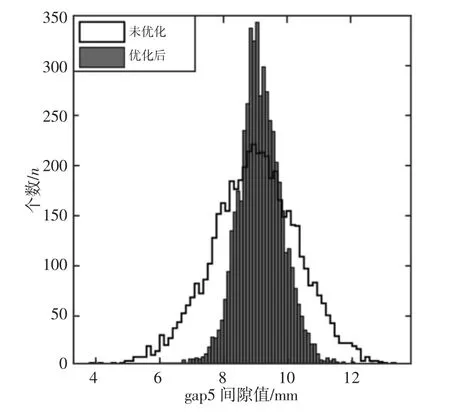
图15 Gap5间隙值优化前后对比Fig.15 Gap5 Comparison Before and After Clearance Value Optimization

经过计算得到，如表2所示。给出了采用装配质量的在线优化控制方法，对铰链安装调整量优化前与优化后Gap1，Gap2，Gap3，Gap4，Gap5的间隙值的波动6σ结果。

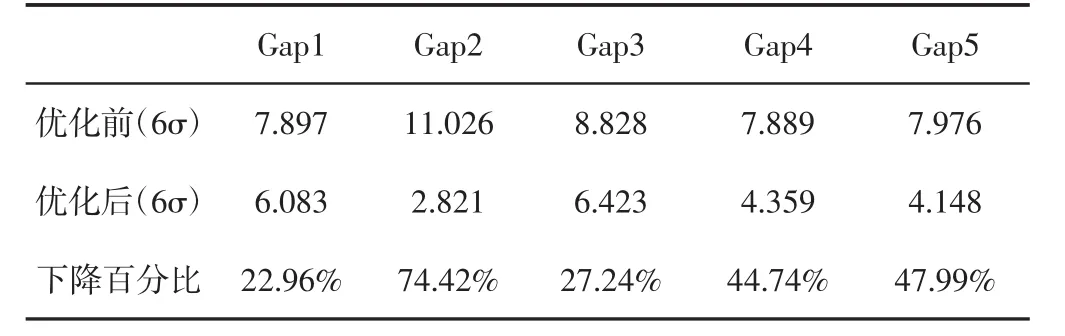
表2 优化结果对比Tab.2 Comparison of Optimization Results

通过对比看出，与不采用优化方法安装比较，采用在线优化控制方法车门安装间隙值6σ值均有明显下降，说明了所采用的装配质量的在线优化控制方法起到了较显著作用。

5 结论

针对装配工艺的在线优化控制问题，这里提出考虑工艺不确定性的车身在线装配工艺的优化控制方法。通过对比简单回归模型、Universal Kriging以及随机Kriging模型的预测性能，验证了存在工艺不确定因素下的随机Kriging模型的预测能力，然后基于随机kriging模型，提出基于前馈控制的工艺参数的在线、优化控制方法，制定了车门装配质量在线控制策略，并通过仿真实验与未经过优化控制的车门装配质量结果进行对比。结果表明，这里对工艺不确定性的车身在线装配精度的优化控制方法具有显著效果，为实际的车身在线装配质量提升提供了理论指导。