基于多尺度排列熵的复合行星齿轮故障诊断研究

武 哲，张 强，黄华蒙 ，成立峰

（1.河北科技大学机械工程学院，河北 石家庄 050018；2.中国北方车辆研究所车辆传动重点实验室，北京 100072）

1 引言

行星齿轮传动系统具有承载大、工作效率高、结构复杂等独特特点，被广泛用于风电机组、重载车辆和武装直升机等重要民用和军用装备的传动系统。据资料统计在行星齿轮传动系统中太阳轮和行星齿轮等零部件发生故障所占的比例较高。因此，保障行星齿轮传动系统中齿轮等关键零部件安全稳定的运行是避免机械设备发生事故的直接手段。利用先进的设备的状态监测方法与技术对齿轮故障的发生原因和位置进行诊断和分析，在此基础之上开发行之有效的行星齿轮传动系统故障诊断方法，对于机械设备健康管理与维修保障技术的发展具有重要意义[1-3]。

针对行星齿轮的故障诊断，文献[4]建立含故障的行星齿轮变速箱的振动信号模型，并通过实验数据进行验证了信号模型的有效性。文献[5]建立了行星齿轮变速箱动力学模型，研究结果证明了齿轮间隙等非线性因素对行星齿轮传动的动力学响应有显著影响。文献[6]考虑了传输路径的时变效应，建立了行星齿轮组的动力学模型，得到了行星齿轮组剥落故障的动态响应。

当行星齿轮传动系统发生耦合故障时，监测得到的的动力学响应信号即振动信号发生相应突变，但是在振动信号的时域图中很难准确识别这一变化。排列熵（Permutation Entropy，PE）[7]作为信号序列复杂性和不确定性测量的有效工具，对机械系统响应信号的微小变化具有较强的敏感性[8-9]。文献[10]提出了一种基于EEMD排列熵和改进的SVM的电机轴承故障检测模型，试验信号分析结果表明了方法的有效性。单一尺度排列熵在行星齿轮故障信号提取方面有着明显的不足为了解决这一问题，Costa提出了多尺度排列熵（Multi-Scale Permutation Entropy）[11-12]，MSPE 可以同时测量多个不同尺度信号的排列熵，对多个系统状态进行同步度量与分析[13]。针对传统时域分析方法难以识别齿轮故障状态的问题，文献[14]提出了一种基于张量核范数正则多元分解和多尺度排列熵的齿轮故障分类联合诊断方法，在实际运行状态下分类准确率为98%。文献[15]提出了基于改进的局部均值分解、多尺度排列熵和Hidden Markov的旋转机械故障诊断模型，该方法在样本数量、训练样本速度和故障诊断成功率等方面具有一定优势。文献[16]提出了一种基于局部特征尺度分解、多尺度排列熵和径向基函数网络的齿轮故障诊断方法，分析表明该方法能准确有效地识别齿轮故障模式。

多排行星齿轮传动系统的复合故障响应特征比单排行星齿轮系统单一故障响应更为复杂，然而，目前发表的关于基于动力学模型的行星齿轮复合故障诊断方面的研究较少。基于上述分析，针对复杂路面激励条件下多排行星齿轮系统复合故障的提取问题。提出了基于动力学模型和多尺度排列熵的行星齿轮传动系统复合故障故障诊断方法。首先建立了多排行星齿轮箱体复合故障的动力学仿真模型，对行星齿轮复合故障状态下行星齿轮系统的动态响应进行了分析，并利用对振动信号突变特征敏感的多尺度排列熵对故障信号进行了分析，结果表明方法可以有效地诊断多排行星齿轮系统的故障类型。

2 三级行星齿轮动力学仿真模型

利用Solid Works建立三排行星齿轮箱的三维模型参数，如表1所示。使用Solid Works自带工具库，设置各个参数，生成标准齿轮和齿圈，进行机械装配，得到各排行星齿轮系。通过对比真实行星齿轮箱，修正各个零件，然后进行装配，最终得到的三维模型，如图1所示。将行星齿轮箱三维模型导入ADAMS软件，通过添加所有部件的材料属性，设置接触约束和齿轮副，在输入轴处添加驱动力，啮合齿轮之间为接触力参数和摩擦系数，如表2、表3所示。三级行星齿轮箱的动力学模型，如图2所示。

表1 行星齿轮箱各排参数Tab.1 Planetary Gearbox Parameters

图1 三级行星齿轮箱三维模型Fig.1 Three-Dimensional Model of Two-Stage Planetary Gearbox

表2 接触力参数Tab.2 Contact Force

表3 库仑摩擦力系数Tab.3 Coulomb Friction Coefficient

图2 行星齿轮箱动力学模型Fig.2 Dynamic Model of Gearbox

3 多尺度排列熵

相比于排列熵，多尺度排列熵可以从多个尺度上计算和测量序列的复杂度和不确定程度，可以准确地反映动力学系统振动响应的微小突变行为，具有明显的优势，多尺度排列熵算法具有较高的灵敏度，非常适合对机械设备振动响应信号的处理与分析，设有时间序列 X=｛x（i），i=1，2，…，n｝，首先，多尺度排列熵算法对时间序列X进行多尺度粗粒化。

4 数值仿真

建立太阳轮断齿和行星轮断齿复合故障的数值仿真模型，时域图与频谱图，如图3所示。在数值仿真信号中添加了干扰信号，但还是可以看出时域图有一定的周期波动性。如图3（b）频域图所示，在啮合频率707.2Hz处和啮合频率叠加行星轮故障特征频率740.9Hz处，以及啮合频率叠加太阳轮故障特征频率825.1Hz等处有明显峰值，并且在峰值周围还有一定的边频带。这说明了行星轮和太阳轮复合故障下，故障行星轮以及故障太阳轮在与其它轮齿进行啮合时产生了啮合振动，这些振动导致了以啮合频谱为中心以故障频率为间隔的边频带处的峰值明显大于正常信号[17-18]。

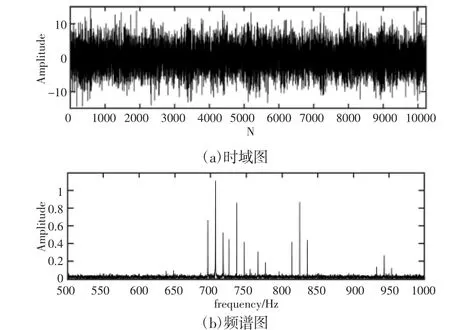
图3 复合故障的时域和频谱图Fig.3 Time Domain and Spectrum Diagram of Composite Fault

5 三级行星齿轮箱故障诊断研究

5.1 随机道路谱

随机道路谱可以模拟车辆实际的运行状态，是一种随机、多变的模型，运用正态分布的路面谱形式，通过MATLAB编程并输出得到路面谱模型数据。将此随机道路谱模型的数据导入ADAMS软件中的动力学模型上进行仿真分析，便可得到在路面激励下的行星齿轮箱的运行状态。

5.2 故障轮齿动力学模型的建立

应用ADAMS建立故障轮齿动力学模型，行星齿轮和太阳轮复合故障位置，如图4所示。三级行星齿轮箱故障特征频率，如表4所示。

图4 行星齿轮和太阳轮复合故障位置示意图Fig.4 Compound Fault Location Diagram of Planetary Gear and Sun Gear

表4 行星齿轮箱故障特征频率Tab.4 First Row Characteristic Frequency of Planetary Gearbox

5.3 仿真结果分析

行星齿轮正常状态的时域和频谱图和行星齿轮单一断齿的时域和频谱图，如图5、图6所示。ADAMS仿真得到的复合故障下振动加速度时域图和频谱图，如图7所示。如图5（a）和图6（a）所示，行星齿轮运行时的振动信号时域图波形具有明显的周期性波形。由图7（c）可知，在啮合频率707Hz，啮合频率叠加行星轮故障特征频率674Hz、740Hz处，啮合频率叠加太阳轮故障特征频率568Hz、824Hz处，具有明显峰值。可见故障轮齿对啮合频谱有很大影响。ADAMS仿真得到的在路面激励下复合故障振动加速度时域图和频谱图，如图7所示。由图可知虽然有一定的周期性，但对比于无路面谱的情况下还是稍有不同，反映了路面激励对行星齿轮箱运行状态有一定的影响。从局部频谱图上看，在啮合频率707Hz，啮合频率叠加行星轮故障特征频率674Hz、740Hz处，有明显峰值，但显然比无路面谱情况下相差很大，更接近实际运行状况，这说明了路面激励下的研究对故障分析有一定影响。

图5 行星齿轮正常状态的时域和频谱图Fig.5 Time Domain and Frequency Spectrum of the Normal State of Planetary Gears

图6 行星齿轮断齿的时域和频谱图Fig.6 Time Domain and Frequency Spectrum of Planetary Gear Breaking

图7 复合故障的时域和频谱图Fig.7 Time Domain and Spectrum Diagram of Composite Fault

图8 路面激励下复合故障的时域和频谱图Fig.8 Time Domain and Spectrum Diagram of Composite Fault Under Road Surface Excitation

5.4 基于多尺度排列熵的行星齿轮故障诊断

时间序列数据的长短直接影响多尺度排列熵的计算结果的准确性，较短的时间序列数据会导致计算结果失稳，过长则会导致运算成本的增加，为此，计算了不同长度的行星齿轮正常状态振动响应的多尺度排列熵结果，如图9所示。不同序列长度的熵值趋势基本一致，当序列长度大于5000时，多尺度排列熵趋于稳定。考虑计算时间与计算结果精确性，时间序列长度选为10240。行星齿轮箱不同状态下的多尺度排列熵，如图10所示。从图中可以看出尺度因子（1～15），三种状态的排列熵有明显增大的趋势，熵值比较接近，无法通过熵值的大小区分三种不同状态，在尺度因子大于15，排列熵相对平稳，走势趋于平缓，此时，三种状态的多尺度排列熵有明显的差距，存在着正常状态＞单一故障＞复合故障的特点，说明随着，通过多尺度排列熵可以对较好的区分行星齿轮传动系统的状态。

图10 行星齿轮箱不同状态下的多尺度排列熵Fig.10 Multiscale Entropy of Planetary Gearbox Under Different Conditions

表5 正常状态和故障状态行星齿轮箱多尺度排列熵的差异Tab.5 Differences in Entropy of Multi-Scale Alignment Between Normal Planetary Gearbox and Fault Planetary Gearbox

6 总结

在所建立的行星齿轮断齿故障和太阳轮断齿故障的复合故障模型的基础上，建立了考虑路面随机激励下的行星齿轮箱复合故障动力学模型，利用多尺度排列熵对齿轮箱正常、断齿故障和复合故障时的振动信号进行了对比分析，通过对处于不同状态的行星齿轮箱进行分析，对比了普通状态下和路面激励状态下的振动情况，得出了相应状态下的时域图和频谱图。研究添加了路面激励下的情况，得到的结果更加接近现实。通过排列熵的方法进行行星齿轮故障的研究，对比不同长度时间序列多尺度排列熵的比较找到一个更加准确的尺度，并在该尺度的基础上进行研究。结果显示行星齿轮箱不同状态下的多尺度排列熵存在着正常状态＞单一故障＞复合故障，发现行星齿轮箱正常振动信号的多尺度排列熵值要高于单一断齿和复合断齿故障信号，熵值平均高出约5.3%，单一断齿的多尺度排列熵高于复合断齿故障信号，熵值平均高出约7.4%。研究结果证明，多尺度排列熵可以有效地诊断多排行星齿轮系统的故障类型。