自适应神经模糊双电位计零死区高精度舵机

罗 虎，贾瑞清

（中国矿业大学机电与信息工程学院，北京 100083）

1 引言

舵机是一种位置（角度）伺服的驱动器，适用于那些需要角度不断变化并可以保持的控制系统[1]。目前，在高档遥控玩具，如飞机、潜艇模型，遥控机器人中已经得到了普遍应用。同时舵机广泛应用于多关节机器人，玩具车船，直升机等，具有较好的可靠性和扩展性[2]。

传统的舵机控制方式是通过接收单片机或其他硬件产生的不同脉宽的PWM波进行舵机输出转角的控制[3-4]。其精度受控制器产生PWM脉宽宽度的精度影响，同时还会带来由于依赖于PWM发生器控制的扩展性问题，难以做到多个舵机串行控制；而采用的控制算法通常是经典PID，这也使得舵机角度输出不稳定，震荡等问题难以解决[9-12]。目前控制性和扩展性，最好的舵机产品之一是韩国ROBOTIS系列舵机，可以单根控制线同时串联多个舵机（理论上能串联255个舵机），同时该舵机做到了360°转角位置输出，但也因其角位移反馈方式采用的绝对编码器而使其价格昂贵，控制器MCU性能要求高等问题，导致单个舵机价格高达数千元，并且由于其控制方式依旧是经典PID，重载时的不稳定问题依然存在[5-8]。

基于此，研究开发的舵机采用了新的控制算法，即自适应神经模糊算法，通过单总线通信方式获得转角指令，设计双电位计角度传感器反馈转角的方式，设计神经模糊控制算法进行舵机控制；以低成本代价研发出稳定的高性能的舵机，实现单根总线同时控制多个舵机达到360°无死区转角输出的目的。本研究基于小型舵机，但研究成果同样可为各类舵机及位置伺服系统的设计研发提供理论参考和技术参数及方法指导。

2 单总线双电位计舵机设计

2.1 微型双电位计角度反馈原理及设计

根据电位计角度传感器的技术文档，市场上单个微型电位计能够测量的角度范围最大值为333°，这是由于圆形电位计的物理几何限制决定的，而采用双电位计角度传感器的设计方式，在空间上采用相位差180°同轴安装的方式，同时测量舵机减速器末级输出轴转角，即可克服该测量瓶颈。

2.1.1 微型电位计信号原理及物理安装设计

微型高精度电位计角度传感器电路，如图1所示。

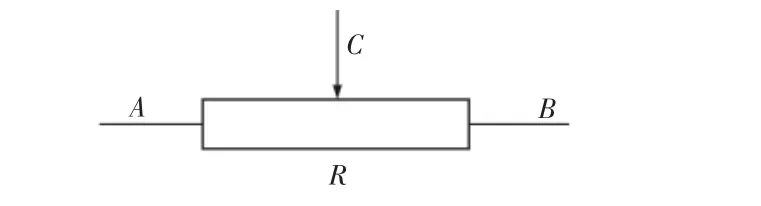
图1 高精度角度传感器电路模型Fig.1 High-Precision Angle Sensor Circuit Model

图中：A端、B端—接参考电压的正负极；

C端—角度模拟电压输出。

该角度传感器的电压信号与转角信号的对应关系为（1），其中Vout角度模拟电压信号输出值，θ表示电位计角度传感器的模拟转角位置值，对应C滑动端子在电阻R上的位置。Kφ表示该角度传感器的比例系数，由关系（2）决定，即加载到传感器上的参考电压Vref和最大可测角度θmax之比。

在PCB电路板上设计同轴放置俯视图，如图2所示。电位计角度传感器的下表面均为接触PCB电路板的一面，PCB电路板设计轴测图，如图3所示。

图2 双电位计电路板俯视图Fig.2 PCB Board Top View

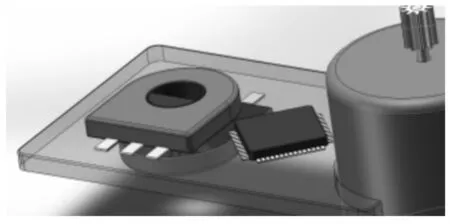
图3 双电位计电路板轴测图Fig.3 PCB Board Axonometric View

将角度传感器依照图2的位置关系平移出来，如图4所示。电路板上表面传感器为SOR1，电路板下表面传感器为SOR2，当减速器输出轴穿过两电位计传感器的驱动孔时，易得两电位计有180°相位差，即：

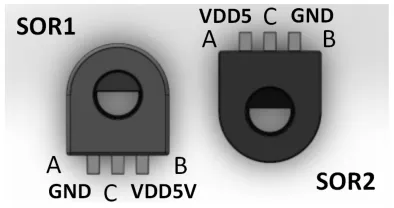
图4 双电位计参考电压加载方向Fig.4 Reference Voltage Direction of Dual Potentiometer

2.1.2 双电位计电气信号加载方式及测量原理

根据上述角度传感器的安装方式以及角度传感器的参数，可以得到该双电位计角度传感器的相图，ABCDEF是电路板上表面的角度传感 SR1 的相图，如图 5 所示。A′B′C′D′E′F′是电路板下表面角度传感SR2的相图，如图6所示。∠AEF和∠A′E′F′是电位计的死区，大小为27°，可测量范围为333°，即弧ABCDE与弧 A′B′C′D′E′所对的圆心角：0°→333°；角度传感器被驱动转向为顺时针方向，参考电压加载方向为正逻辑方向，即角度为零点的角度模拟电压输出值也为零，最大可测角度333°输出参考电压值5V（本设计的参考电压是5V）；为了使得两传感器被减速器输出轴同时驱动时，两转动角度均从0°向333°增大的方向变化且角度模拟电压反馈值也向着参考电压的5V方向递进，故将下表面电位计的参考电压加载方向与上表面电位计相反，设计参考电压VDD5V与GND加载方式，如图4所示。

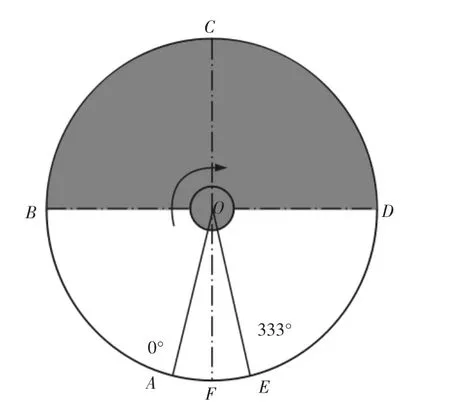
图5 上表面角度传感器SOR1Fig.5 Up SOR1 Phase Diagram

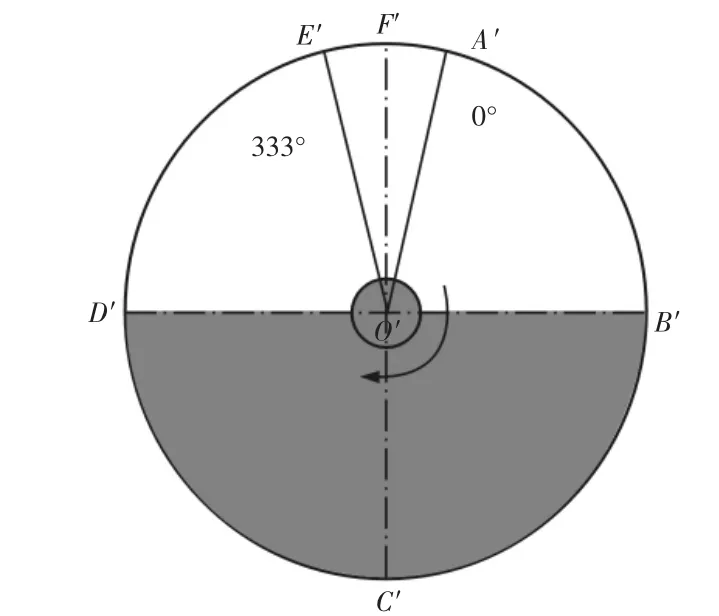
图6 下表面角度传感器SOR2Fig.6 Lower SOR1 Phase Diagram

两电位计角度传感器同轴焊接到电路板上，如图2所示。重叠相位图，如图7所示。上表面ABCDEF角度传感器SOR1，下表面 A′B′C′D′E′F′角度传感器 SOR2，由于两电位计参考电压加载方向是相反方向，如图4所示。故，当减速器末级输出轴顺时针驱动两电位计旋转时，两传感器输出的转角模拟电压信号均朝着增大的方向（本设计的参考电压是5V，故模拟电压输出范围是从0V到5V），同时角度也是从0°向着333°线性增大，满足关系（1），即：

2.1.3 双电位计角度取信区间以及关系分析

设计两传感器的取信角度区间以及关系，如图7所示。设A点减速器轴转动零点，顺时针转动一圈，则上表面角度传感器ABCDEF 角度变化为 0°→333°→333°+27°，即 0°→360°，根据关系（2）映射下表面角度传感器 A′B′C′D′E′F′角度变化为 0°+180°→180°+（180°-27°）→180°+153°+27°+180°，180°→180°+360°；故两传感器的死区（27°）亦总是满足180°相位差关系，故理论上讲，减速器旋转输出轴以死区外任意位置作为旋转起点，均可得到以A点为起点相同的结论，即交替度过死区，弥补单电位计角度传感器不能整周测量反馈的限制。的上下半圆弧分成两个半圆区间，分别取信上下两电位计的角度反馈值，即可完成对减速器输出轴的转角整周反馈，即以B点（亦D′点）为输出轴旋转起点，角度取信区间如下：

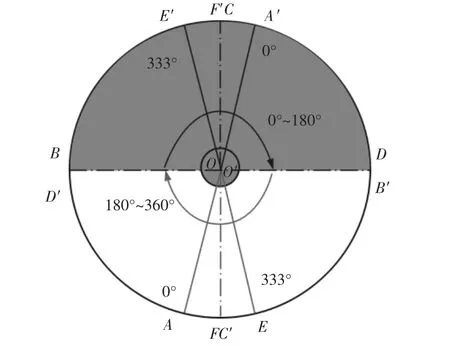
图7 双角度传感器重合相图Fig.7 Double Angle Sensor Overlapped Phase Diagram

可见，两角度传感器的反馈模拟电压值区间左右端点值相同，但由于两个传感器是同轴驱动旋转的，故两传感器不会同时反馈回来该区间的数值，即两个角度模拟数据反馈回控制器后，同一时刻有且仅有一个出现在区间（6）或者（7）中，通过判断位于区间内的传感器是Vθ1还是Vθ2，即可得到减速器输出转轴的准确位置。

2.2 电路设计

为实现单总线双电位计自适应模糊神经网络舵机系统，在硬件电路上设计半双工串行电路以及其通信协议，上位机直接发送指令给舵机控制器的串口端，舵机控制器MCU校验地址命令后进行驱动输出角解析，然后舵机控制器通过双电位计获得舵机实际输出轴转角，以偏差以及偏差的变化作为模糊神经算法的输入，将算法输出作为舵机运动输出的控制量；此设计方案使得舵机主从控制性能极大的提高；由于神经模糊算法对内存要求较高，故外扩一片RAM；限于篇幅，在此只给出单总线通信电路以及双电位计角度传感器电路设计。

2.2.1 单总线通信电路设计

采用74HC126逻辑门芯片，实现单总线信号输入和输出的方向控制，如图8所示。单片机的10引脚与11引脚控制信号出入，UART为TTL单总线，RXD与TXD分别连接到单片机的输入输出串口引脚。当需要同时控制多路舵机时，只需要将各舵机的单总线串接并上拉合适的驱动电流即可。

2.2.2 双电位计角度传感器电路设计

采用两个TZ12-103A333D40-30中空轴微型角位移传感器，如图9中AngleCoder_1_与AngleCoder_2_，分别将Vdata引脚角度模拟电压信号接入ATmega8A单片机的23与24模拟数字信号转换引脚，设计参考电压，去噪电路。

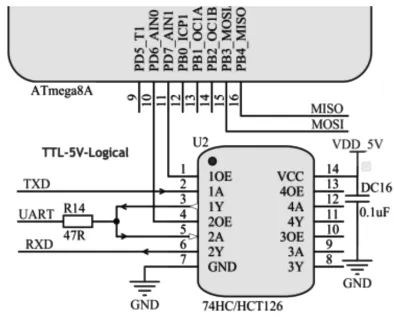
图8 单总线电路Fig.8 Single Bus Circuit

图9 双电位计角度传感器电路Fig.9 Dual Potentiometer Circuit Design

2.2 .3电路板制板及样机

制作的电路板，舵机设计供电电压为9V，舵机仅由一根单总线控制，其余就是电源线和电源地线，如图10所示。减速器装配样机，如图11所示。引脚功能说明如图中标识。

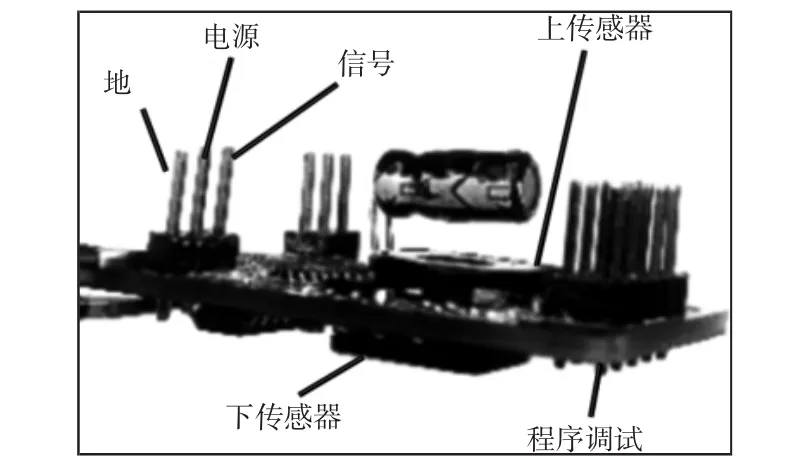
图10 制作电路板Fig.10 PCB Board Manufactured

图11 样机Fig.11 Prototype

3 自适应模糊神经网络控制系统设计

舵机主要应用在需要位置伺服的场合，在负载力矩作用下，舵机响应的非线性特性也主要出现在位置环上，速度环并不敏感，在此就不做考虑；传统的PID算法对负载变化时反应敏感，难以满足控制要求，故引入自适应神经网络控制算法以求得到相比传统PID算法更好的控制效果和稳定性能。在本研究设计的双电位计角度传感器舵机系统的硬件基础上，实现自适应模糊神经网络算法控制。

舵机运行过程中，通过双电位计角度传感器实时获得输出轴的转角，数据经过单片机计算处理，得到舵机输出距离目标角度的误差以及误差的变化，将两个计算量作为舵机系统的控制算法的输入，经模糊神经网络对控制参数实时调整，获得最优参数后，输出控制量。

显然，与传统的PID算法直接采用误差和误差变化信息不做其他处理，仅作用一定的权重就输出控制量相比，此方法考虑的信息和因素更多，在不同负载作用下，舵机系统能表现出更稳健的性能，即在系统硬件和软件参数受到环境和本身的温升变化等非预测性变化因素作用下，具有更高的动静态性能和鲁棒性[14]。

3.1 自适应神经网络控制算法简介

神经网络结构依据其联接方式的不同分为前向网络（前馈网络），反馈网络，相互结合型网络和混合型网络。在本研究针对双电位计舵机采用的是前向网络，前向网络结构图，其特点是共有三层网络，如图12所示。且只有前后相邻两层之间的神经元相互有连接关系且各个神经元之间并没有信号反馈，每个神经元可以接收多个输入并仅只有一个输出送给下一层的每一个神经元。三层网络分别称为输入层，隐含层和输出层；输入层不具有计算功能，且输入层中神经元节点数总和就是输入信号数量，这里输入信号有三个，分别是系统参考角度rref系统的输出角度Y（t），和自适应算法的上一个输出信号u（t-1）；隐含层和输出层的神经元具备计算功能，这里的隐含层取四个神经元节点，输出层同样依据实际硬件条件和精度要求确定，这里为说明简单只取一个，即，此神经网络输出的控制作用信号只有一个。相邻两层之间有前一层各神经元输出信号的最终作用强度大小的衡量，即图中所示的权重系数I和权重系数II，自适应算法的核心就在于改变这两组权重的大小，自适应算法输入量为误差e（t）。

这里设每个神经元的数学激励函数为fi，权重系数为wij；神经元的输入作用信号为zj；偏移量为bi；则可将每个神经元的输出方程表示为：

为符合神经元模型处理神经冲动的特性，激励函数必须具有突变性和饱和性，即满足模拟神经元兴奋过程中的神经冲动和疲劳特征。基于此，选择的激励函数也必然是非线性的。为方便处理，隐含层和输出层都采用Tan-Sigmoid双曲正切S型函数，其特点是在无穷域上连续可微，类阶跃和零均值，值域为（-1，1）[15]。

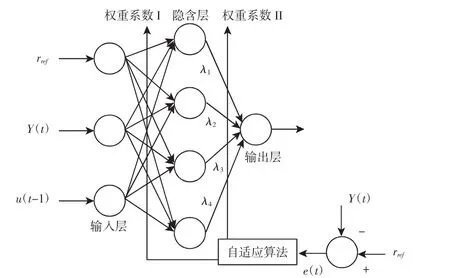
图12 自适应神经网络结构图Fig.12 Adaptive Neural Network Topology

自适应神经网络算法的作用体现在它对系统各种状态下响应并对神经网络各层之间的权重系数在线改变的过程中，使神经网络输出最优值；它基于Widrow-Hoff自适应算法，具体的学习规则是Delta规则，此学习规则旨在于不断的改变权重系数I和II，直到期望参考舵机的角度指令和实际偏转角度Y（t）的方差值达到最小。

令输入向量为z，t时刻权向量为W（t），t+1时刻的权向量为W（t+1），换算系数为α，则权向量随时间变化的关系可表示为[9]：

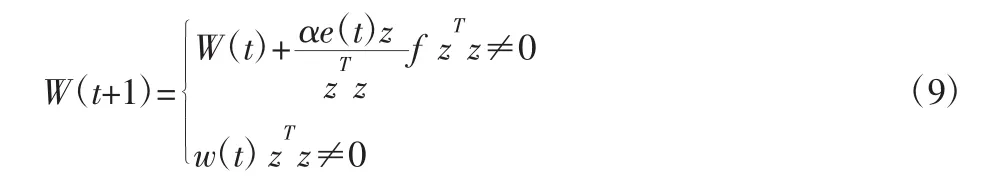
式中：当且仅当 0＜α＜2，误差收敛。

3.2 自适应模糊神经网络控制算法设计

在研究的双电位计反馈舵机硬件系统的基础上，研究设计完全的自适应控制人工神经网络算法，并耦合模糊逻辑控制，组成自适应的模糊神经网络以达到算法系统可自动调整比例因子的目的，其拓扑结构设计，如图13所示。

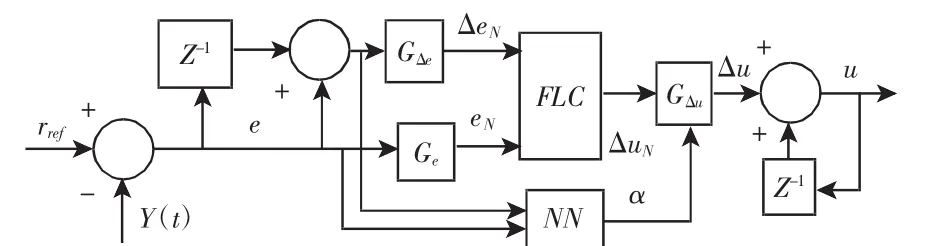
图13 模糊神经网络算法拓扑结构图Fig.13 Fuzzy Neural Network Algorithm Structure Diagram

模糊神经网络算法的两个输入分别是参考角度rref和系统实际输出角度的反馈量Y（t），两变量代数运算得到角度误差e（t），以及角度误差的递增量 Δe（t），即有式（10）：

两个输入比例增益器Ge和GΔe，根据传递函数关系，两比例增益器的输出信号eN和ΔeN可以表示为：

FLC是模糊逻辑控制器，其输入信号分别是比例增益器Ge和GΔe的输出量eN和ΔeN，其输出信号表示为ΔuN；NN是神经网络控制器，其输入信号是误差e（t）和误差的递增量Δe（t），其输出信号是一个调整因子α；FLC模糊逻辑控制器和NN神经网络控制器的输出通过耦合器GΔu耦合，耦合器GΔu的作用是综合两控制器的控制效果，对控制信号进行动态调整并输出调整量作用信号Δu；系统输出最终控制信号为u；即有如下信号传递和变化关系：

3.2.1 模糊逻辑控制器FLC

本研究设计的是一个二维的FLC模糊逻辑控制器，模糊变量和论域是仿真综合选择并最终确定的，隶属函数离线定义；输入模糊变量为误差eN和误差递增量ΔeN，输出变量为调整量作用信号ΔuN，根据本研究设计双电位计舵机系统输出精度和性能综合要求，模糊变量和论域分别定义如下：

为了使舵机整体体积小，本研究设计采用的单片机控制器选择小封装导致Flash和RAM大小有限，复杂的隶属函数会引起运算量的急剧增加带来的时间和空间耗费对舵机系统在线实时优化产生不利的作用，因此本算法中采用较简单的三角形隶属度函数，方程表示如下：

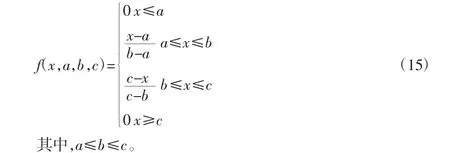
3.2.2 神经网络NN

在双电位计舵机硬件条件下设计神经网络拓扑，如图14所示。采用输入层节点2个，隐含层节点3个以及输出层节点1个的三层前向神经网络结构。两个输入信号分别是误差e（t）和误差递增量 Δe（t），输出信号为调整因子 α，其值域为（-1，1）。

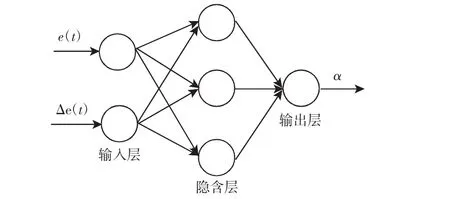
图14 神经网络拓扑结构图Fig.14 Neural Network Topology

取隐含层节点激励函数：

输出层节点激励函数：

故，模糊神经控制算法的输出信号u（x）在经模糊控制器FLC和神经网络NN重新调整后用来调制电动舵机的位置环控制量。

3.3 双电位计反馈仲裁及滤波

双电位计角度传感器物理上反馈回来两个角度数值，程序分别读取两个数据，数据经过滤波后放入取信区间式（6）和式（7）进行判断，由于两个角度传感器输出关系满足式（3），故两个角度值时刻有180°相位差，必然不会同时满足区间式（6）和区间式（7），所以两个传感器中任何一个传感器反馈数值任意时刻必有一个位于两区间之一，在程序设计中都仅需判断一个值就可确定另外一个角度传感器的值状态。

递推均值滤波：为了获得更加准确的舵机减速器末端轴输出的转角位置，对两角度传感器反馈值位于有效区间时分别进行递推均值滤波，以获得更好的控制效果。单片机采集N个角度值，排成一个队列数组，每进行一次采集，便把测量值放在队尾而把队首的值覆盖，然后队列数组的N个数据进行算数平均后的值作为滤波值输出，本次算法设计中采集窗口长度N为13，即：

在获得输出轴经滤波之后的转轴位置后，再计算误差e（t）和误差递增量Δe（t），作为自适应模糊神经网络算法系统的输入。

4 仿真与试验

以Atmel公司的AVR-Atmega单片机做计算控制器，外扩一片串行SOP8小封装的RAM芯片以满足程序算法运行的空间要求，实现双电位计无死区舵机的自适应神经网络控制；双电位计舵机串行级联样机实验系统，如图15所示。样机基本参数如下：直流永磁电机反电动势参数Ke=0.0035V·s/rad，转矩参数Kt=0.0087N·m/A，电机电枢的电阻和电感分别是R=0.238Ω和L=2.4×10-3H，换算到电机输出轴的转动惯量 Jn=2.35×10-6kg·m2；减速器减速比16.3；额定电压U=9V。通过MATLAB/Simulink工具建立了单个双电位计舵机系统的动态仿真模型，如图16所示。限于篇幅，仿真模型不详细说明。

图15 两舵机串行控制实验测试Fig.15 Two Servos Serial Control Experiment Test

图16 舵机系统Fig.16 Matlab Servo Testing System

为了验证双电位计舵机系统在自适应模糊神经网络控制算法作用下的优越性，快速性，仿真系统给定一个10°的舵偏角指令，得到响应曲线，如图17所示。分析可知，对于经典PID（Kp=0.0038，Ki=0.015，Kd=0．33）控制算法，因为三个参数的调节是预先设定的，不具备自整定能力，应对系统激励和惯性负载变化的能力差，所以其拥有较大的上升时间，达到了85.67ms，并且有21%的超调量；而采用自适应模糊神经网络控制算法的阶跃响应时间仅45.86ms左右，且无超调。

图17 舵机系统阶跃响应曲线Fig.17 Servo System Step Response Curve

编写上位机控制软件界面，如图18所示。

图18 舵机上位机控制器Fig.18 Upper Computer Controller

两样机串行测试实验系统，如图15所示。上位机通过命令模式指令使得两个舵机均工作在舵机角度输出方式，再由上位机分别选择 ID=1（0x01）以及输入目标转角，ID=2（0x02）及目标转角，轮流依次发送，测得稳定响应并记录，部分响应的分布情况，如图19所示。输出角度数据及误差计算，如表1所示。

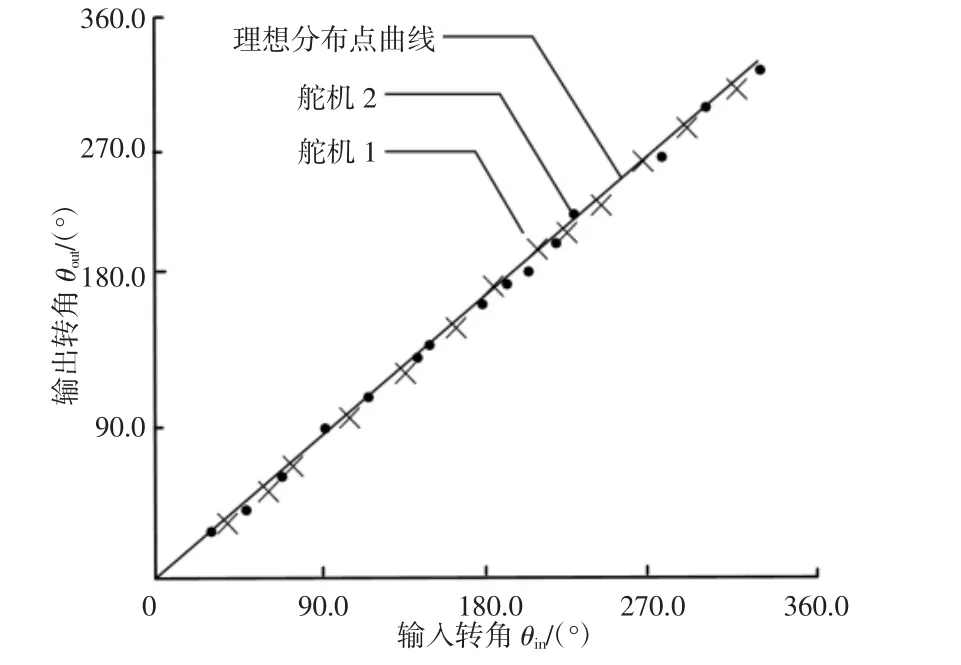
图19 舵机位置测试点分布Fig.19 Servo Position Test Point Distribution

观察响应分布图19可以得到结论：两个自适应模糊神经舵机角度输出响应分布基本位于理想曲线下方，没有出现明显的超调，与仿真结果相符合；从表1中的误差方向（+/-表示实测输出与目标转角的差值的正负，即误差方向）也可以得出与此相同的结论。

表1 多舵机位置输出测试值和误差Tab.1 Multiple Servos Test Values and Errors

误差分析：

单片机AD编码为10位，故测量反馈角度的误差范围，Δ1=333°/1024≈0.333°同时由于每个角度传感器的测量有效范围并非完全的333°，其波动范围也应计入反馈角度误差中，因此获得的转动零点位置的设置值也存在误差Δ2≈0.141°，电路板上角度传感器的AD参考电压5V波动带来的误差Δ3≈0.292°，电位计信号端子的触点接触电阻带来的误差Δ4≈0.292°，减速输出轴与两个电位计角度传感器的传动间隙带来的误差，即Δ5≈0.231°，样机系统考虑制造和装配总误差Δ6≈0.302°，故输出总转角误差为：

实验结果分析：

通过分析得，自适应模糊神经舵机响应转角误差基本位于总误差Δ范围内，且每次舵机角度响应收敛平稳几乎无超调，故认为双电位计角度传感器满足设计要求；分析可知，舵机输出转角误差主要来源于AD值的编码范围，角度传感器本身的准确度和机械系统，故完全可以换更高AD位数的单片机，选用更高精度的电位计角度传感器以及增加机械制造和装配精度，再考虑的补偿逻辑算法，获得更高的整周角度控制精度是完全可行的[13]。

5 结论

本研究首先提出了双电位计角度传感器的总线舵机反馈系统设计方案，在此硬件基础上引入自适应模糊神经网络控制算法对双电位计角度传感器舵机输出转角进行闭环控制，相比绝对编码器和此编码器的舵机的成本优势在此显现出来，在解决了传统PID控制算法带来的不可避免的舵机输出震荡，收敛困难等问题的同时还解决了普通舵机无法实现的360°整周无死角定位问题。通过仿真和样机实验证实了设计的正确性，展示出自适应神经模糊双电位计舵机控制方便，响应无超调等优点，可为实际中设计各种功率输出的舵机产品以及伺服驱动系统提供很好的理论依据和技术指导与参考。