基于最小方差的声线跟踪自适应分层算法

冯国君，单志龙,2，项 婉

(1. 华南师范大学计算机学院，广东广州510631；2. 华南师范大学网络教育学院，广东广州510631)

0 引 言

在高精度水声定位系统中，目标与声源的距离通过声速和传播时延来确定。然而海洋环境复杂多变，声速随温度、盐度和深度变化而变化。此外，声波在非均匀海洋介质中传播时产生折射现象，声线传播规律符合斯涅尔定律，声线向最小声速区域弯曲。因此，在海洋中声线并非沿直线传播，声速并非固定不变。在长距离传输过程中，如果采用恒定声速与传播时延的乘积计算距离容易产生较大误差，对定位精度影响较大。

修正弯曲声线能够减少误差，因此提出了如有效声速法[1-2]、查表法[3]、等效声速剖面法[4]和声线跟踪法[5-11]等多种方法。其中，声线跟踪法基于声速分层假设，利用海洋声速剖面数据，采用分层计算、合计累加的思想对弯曲声线进行补偿[10]。声速分层越多，定位精度越高，但计算量也随之增加，因而需要对声速剖面数据精简。应用等间隔分层或人工筛选等简单分层方法重构声速剖面，不能充分保留原始声速数据特征，分层不尽合理，定位精度不高。针对这个问题，国内外学者提出了多种分层方法。张居成等[5]根据等效声速剖面思想，对声速剖面在指定精度下以最少层数进行非等间距划分，用等梯度分布的声速剖面曲线代替原始声速剖面，简化原始声速剖面。郑根等[6]提出基于面积差约束分层方法，保留声速剖面基本空间结构，实现对声速剖面大幅度的精简。但这两种方法都事先根据声速剖面数据梯度变化点将声速剖面分层，缺乏对剖面结构的全局考虑。张志伟等[7]应用D-P(Douglas-Peucker)压缩算法对声速数据进行压缩，重构声速剖面，其所依赖的数学模型与物理模型不一致，声速变化剧烈时效果不佳。赵荻能等[8]提出了改进D-P算法，将距离意义映射到声速维度上。这两种方法在多波束测深领域取得了良好效果，但未有文献证明其在长基线系统中具有良好的效果。李圣雪等[9]提出了一种适用于深海长基线定位的自适应分层声线跟踪法，通过对声速剖面数据合理精简，合并梯度变化较小的声速层，保留梯度较大的声速层。该方法在确保定位精度的前提下对声速剖面进行精简，但分层数较多，仍然有压缩空间。本文针对分层数与运算量相矛盾的问题，提出了基于最小方差的声速剖面自适应分层算法(Adaptive Division Based on Minimum Variance, ADMV)，通过对原始声速剖面全局搜索，找到最佳切分点，实现了对声速剖面的最优简化，以较少的分层数达到较高的定位精度，同时兼顾了定位时间与定位精度的问题。

1 双曲面解算模型及声线修正方法

长基线定位系统一般采用双曲面交汇模型解算目标位置。假设长基线定位系统由 4个阵元组成，声波从阵元Wj到应答器A(x,y,z)的传输时延为tj，令，则根据双曲面交汇原理可解出目标位置，其求解的方程组为

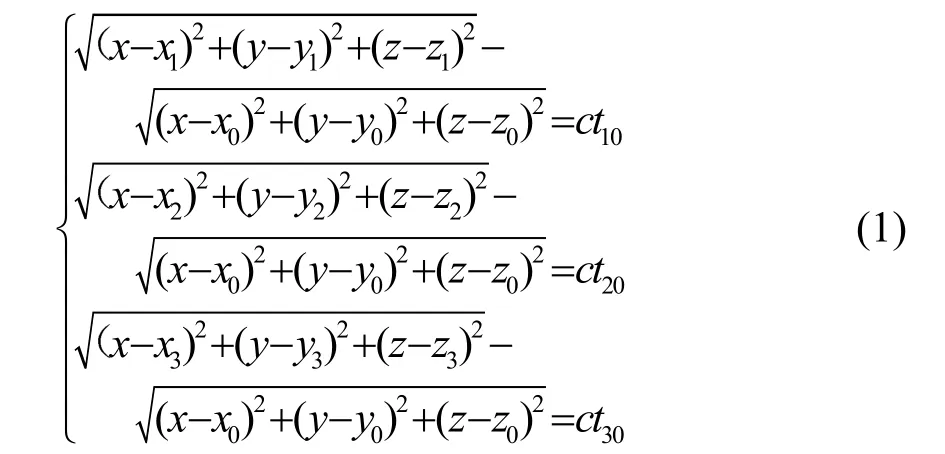
式中：c为恒定声速。声速在水下非均匀分布，使用恒定声速解算会造成较大误差。常梯度声线跟踪算法示意图，如图1所示。假设声速近似由多层简单结构的声速层表示，声速在层内均匀变化，第i层内声速梯度gi表示为

式中：ci为第i层的上表层声速，Δzi为第i层的厚度。声线在层内传播符合斯涅尔(Snell)定理：

式中：iα为声速ci处的掠射角，p为Snell常数。

如图1所示，声线在层内沿曲率恒定圆弧传播，曲率半径Ri为

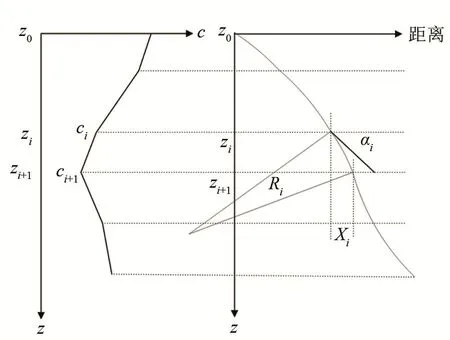
图1 声速常梯度分层假设下的声线跟踪示意图Fig.1 Schematic diagram of acoustic ray tracking under the assumption of layering the sound velocity with constant gradients

根据式(2)～(4)，可得到声线在第i层内的传播时间ti和水平距离xi：

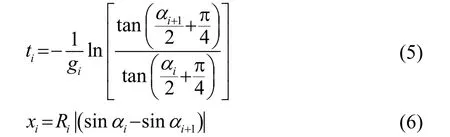
应用声线跟踪理论可以计算出各个阵元到目标的距离差，代入式(1)双曲面解算方法即可解算目标位置。但声线跟踪算法计算复杂，难以求出它的解析式。文献[12]提出了声线修正解算方法，通过逐步逼近的方式对目标位置进行修正。声线修正方法流程如下：

(2) 将计算时间差与实测时间差比较，若小于设定值，则给定坐标作为最终坐标。否则，通过差分方程求解位置的修正量。

(3) 利用求解出的修正量对目标位置进行修正，并以此作为最终的定位结果。

(4) 重复步骤(1)～(3)，直到计算时间差与实测时间差满足阈值条件。

由以上分析可知，长基线声线修正定位算法的复杂程度主要取决于声速分层的层数。应用原始声速剖面数据解算更符合真实水声环境下声波的传播路径，定位精度高，但声线修正的逐步逼近方法需要多次应用声速剖面进行迭代计算，声速层数越多，计算复杂度越高。如果对声速剖面精简处理会导致弯曲声线得不到有效补偿。如何根据声速变化的特点，保留原始声速剖面特征的同时对声速剖面简化，权衡计算复杂度与定位精度间的关系尤为重要。

2 ADMV算法

图2为南海某海域实测声速剖面[13]。由图2可见，在一定深度范围内，声速与深度近似线性相关关系。而常梯度声线跟踪算法假设声速近似由多层简单结构的声速层组成，声速在层内均匀变化。因此，可将原始声速变化线性较强的部分划分为一层，这样既保留了声速剖面在一定区域内呈线性变化的特征，又契合常梯度声线跟踪算法思想，达到简化计算的目的。基于此，ADMV算法采用自顶向下的思想，通过对声速剖面进行全局搜索，在设定阈值的条件下，递归地将声速剖面分成与原始数据差异最大的两段，从而使分开的层内拟合效果更好，更能表现出原始数据的特征。

有时候我也想，这个谢瑞天是不是真的对我动了感情。没错，世界上有钱的男人大把，但世上漂亮迷人的女人更是不计其数。他为什么要在我身上作这么大手笔的投资呢？

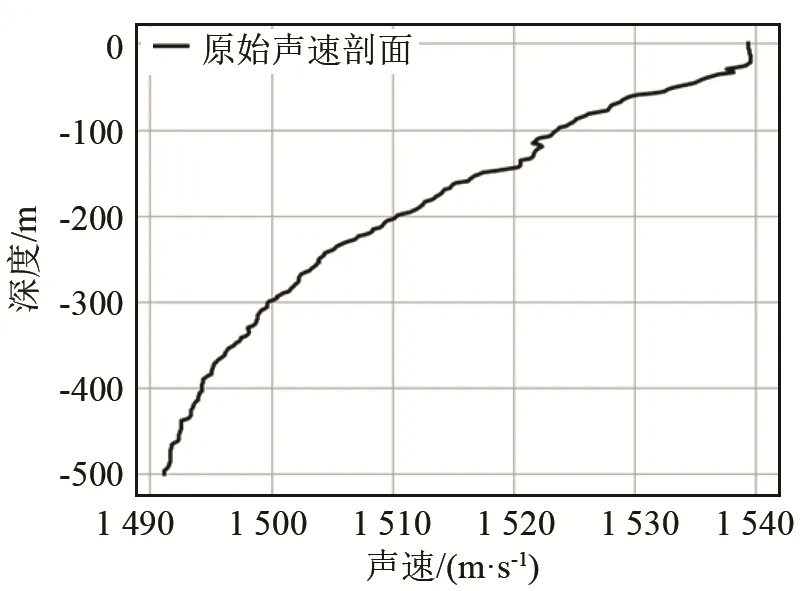
图2 声速剖面曲线[13]Fig.2 Sound velocity profile[13]

ADMV算法分层原理如图3所示。算法具体流程如下：

(5) 对于每个已经分开的声速层，重复步骤(2)～(4)，直至分层结束。

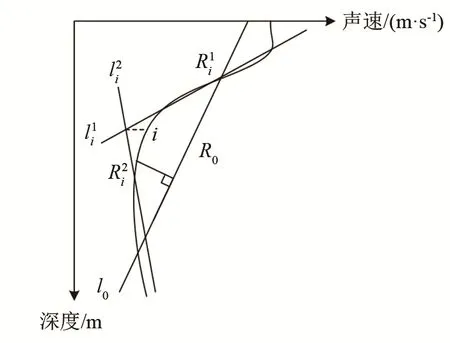
图3 自适应声速分层原理图Fig.3 Principle of adaptive stratification algorithm

ADMV算法是在设定阈值的条件下，对声速剖面进行全局搜索。设定阈值δ作为控制分层条件，表示拟分开的两段与原来的声速剖面的相似程度。阈值的大小直接决定声速剖面分层的层数。如果阈值设置得较大，分层的层数较少，不能很好地拟合原始声速的特点，失去了分层的意义。相反，如果阈值设置得较小，分层的层数较多，导致计算效率降低。因此，在仿真实验中需探索分层数与阈值以及定位精度的关系，找到一个满足条件的最佳阈值。

ADMV算法同时进行自动阈值搜索与定位。首先输入原始声速剖面，执行分层算法步骤(1)～(3)，在步骤(4)中，初始设定R=δ，继续执行分层算法得到重构的声速剖面。通过逼近算法对目标进行定位，并与原始声速剖面定位位置比较，当定位精度与原始定位精度一致则停止搜索，输出阈值、层数与定位精度之间的关系。否则减小δ值，重复以上操作。

3 仿真实验

为了验证 ADMV算法的有效性，本文采用南海某海域 500 m深的声速剖面数据(如图 2)进行定位模拟，其中，声速剖面采样间隔为2 m，实验仿真参数的选取参照文献[5]。在海面部署一个边长为1 600 m的正方形区域，在每个顶点各设置一个浮标，为了模拟海浪对浮标的扰动，在浮标的三维坐标值上各加上2 m的余弦波动。在海底模拟固定4个应答器作为定位目标，以测试重构后的声速剖面对定位造成的影响。它们的坐标分别为(0,0,-500)、(0,40, -500)、(40,0, -500)、(40,40, -500)，单位为 m。由于原始声速剖面采样间隔较小，通过原始声速剖面计算的声线路径更接近真实路径。通过重构后声速剖面与原始声速剖面定位的差别检验分层算法的效果。仿真噪声模拟如下：换能器的定位误差在x、y、z轴方向上各为10 cm，应答器时延造成8 cm的测距误差，测量时间造成10 cm的测距误差。为了对比说明，在满足模拟系统测量误差的环境下，首先利用原始声速剖面数据采用文献[12]的声线修正解算方法对4个应答器进行定位，如表1所示。

表 1中Dx、Dy、Dz分别表示在加入噪声情况下使用原始声速剖面定位时x、y、z轴上的误差，Ds为解算坐标与真实坐标的距离。可以看出，4个应答器在水平方向的定位误差最大为 0.73 cm，最小为0.06 cm。垂直方向的定位误差在20～23 cm的范围内波动。由于采用逼近解算方法计算目标位置，解算位置在水平方向上更接近目标，误差主要集中在垂直方向上，即在深度上存在比较大的误差，水平方向上基本可以忽略不计。表1表明分层算法在系统存在噪声的条件下能达到较高的精度。

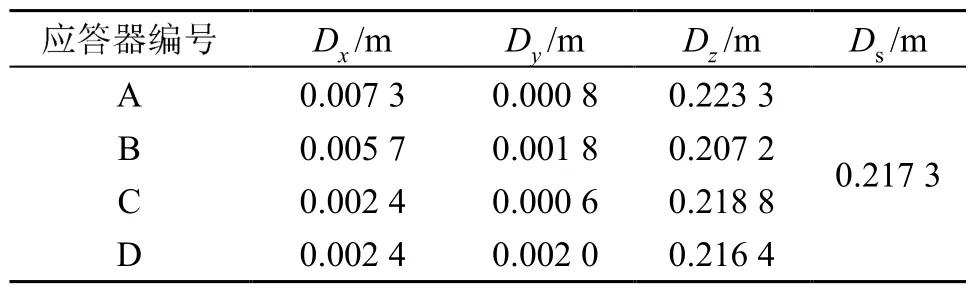
表1 原始声速剖面定位误差Table 1 Positioning errors based on original sound velocity profile

3.1 阈值的选取

图4是声速剖面阈值的选择与划分层数、定位误差之间的关系。随着选取阈值的降低，声速剖面被划分的层数增加，但阈值数值与层数没有绝对的关系，而是随不同声速剖面结构的变化而变化。另一方面，当划分的层数由7层增加到16层时，随着层数的增加，定位误差逐渐下降，当声速剖面被分为 12层时，定位精度与使用原始声速数据定位的精度一致。随后声速分层增加，精度达到系统误差，趋于稳定。产生这种现象的主要原因是划分的层数越大，重构的声速剖面越接近于原始的声速剖面，定位精度也越高。

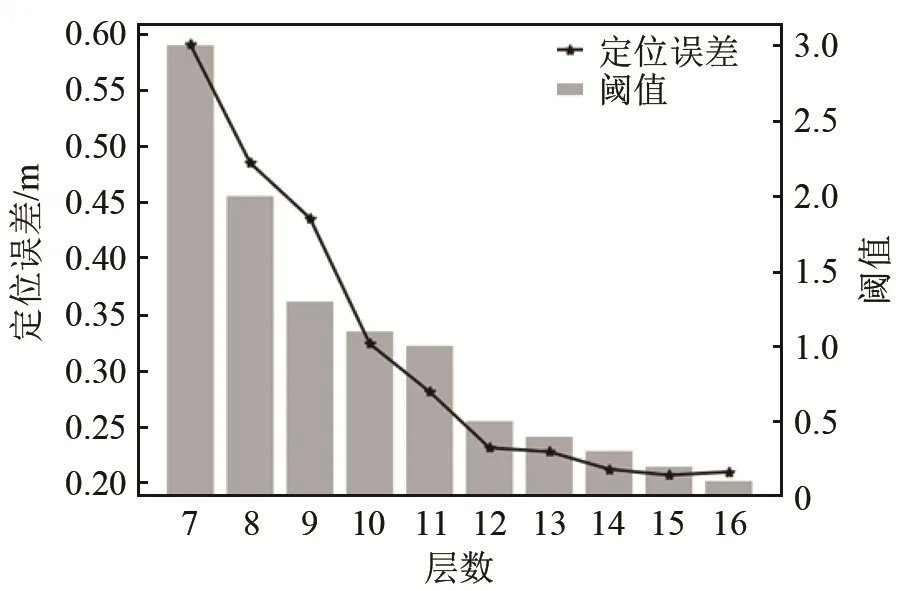
图4 定位误差、阈值和声速剖面分层数的关系Fig.4 Relationship between positioning error， threshold and the number of sound velocity profile layering

图5为在不同阈值条件下，运用ADMV算法对声速剖面进行分层的情况。图5(a)～5(f)分别为声速剖面被划分为7～12层所对应的剖面图。由图5可见，一方面，随着划分层数的增加，重构声速剖面与原始声速剖面越来越吻合，当被划分为 12层时，拟合的效果达到最佳。另一方面，原始声速的变化随着深度的增加而线性变化的规律更强，声速变化较大的区域主要集中在 0～380 m的深度范围内，深度380 m以下的区域内声速变化趋于平稳，呈近似线性变化的趋势。因此，随着阈值减小，声速剖面被划分的层数增加，划分区域主要集中在声速变化较大的表面层。这样重构声速剖面尽可能保留了原始声速剖面的特征，重构声速剖面与原始声速剖面更加吻合，使得定位误差逐渐减小。

3.2 误差比较

为了验证ADMV的性能，本节对D-P算法[4]、等间隔分层算法和本文算法进行了定位精度的对比。D-P算法通常用于对高度复杂的多线段进行简化，等间隔分层算法是声线跟踪常用的一种分层算法，通过将海洋深度等间隔划分从而实现声速剖面重构。如图6所示，层数从5层增加到30层时，3种分层算法都是随着层数增加，定位误差降低。等间隔分层算法定位精度由于受层数影响较大，分层方式过于简单，不能反映声速剖面的特征，定位误差高于D-P算法和ADMV算法。D-P算法采用声速散点到首尾声速点连线的最大距离作为分层条件，缺少对声速剖面的全局考虑，容易受到测量误差的影响，因此其定位误差高于 ADMV算法，但低于等间隔分层算法。ADMV算法通过对声速剖面进行全局搜索，采用全部声速散点来拟合直线距离，从而寻找最佳拆分点，因而在所分层数相等的条件下，定位精度明显高于其他两者。

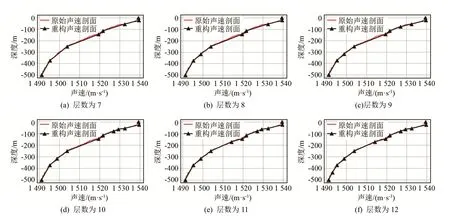
图5 不同分层数的声速剖面划分图Fig.5 Stratification diagram of the sound velocity profile with different number of layers

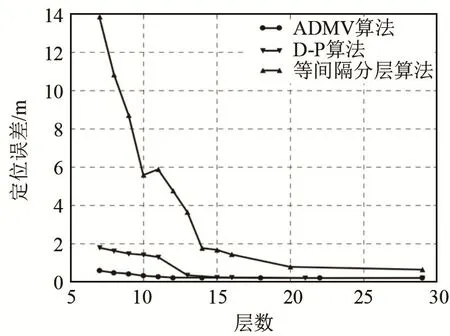
图6 不同算法声速剖面分层数与定位误差的关系Fig.6 Relationships between the number of sound velocity profile layering and the positioning errors for different algorithms

3.3 定位时间

定位时间取决于声速剖面所划分的层数，层数越多，定位消耗的时间就越长，定位效率降低。为了验证 ADMV算法在定位时间上的优势，本节将长基线定位的自适应分层声线跟踪算法[5]与本文算法进行对比。实验中使用型号为四核 Core(TM)i3-2350M、主频为2.30 GHz的处理器。如表2所示，随着划分层数的增加，两种算法的定位时间均不断增加。长基线定位的自适应分层声线跟踪算法当分层数从 64层加到 197层时，定位误差均保持在20 cm左右，消耗的时间从31.5 s增加到97.6 s。而ADMV算法当分层数从7层加到15层时，定位误差从59 cm降低到21 cm，消耗的时间从2.8 s增加到3.6 s。可见，达到相同稳定的定位误差20 cm左右时，声线跟踪算法划分的层数为 64层，消耗的时间为31.5 s；ADMV算法划分的层数为15层，消耗的时间为3.6 s。造成这种现象的主要原因是长基线定位的自适应分层声线跟踪算法将声速剖面n个数据点进行3次多项式拟合，计算声速点的曲率以确定是否合并声速剖面，保留主要声速层以减少运行时间，但它是基于局部搜索，将声速相邻几层进行合并，导致重构声速剖面层数较多。而ADMV算法是基于整个深度范围的全局搜索，用较少的层数就可以保留原始数据特征，从而可以大大地减少定位时间。

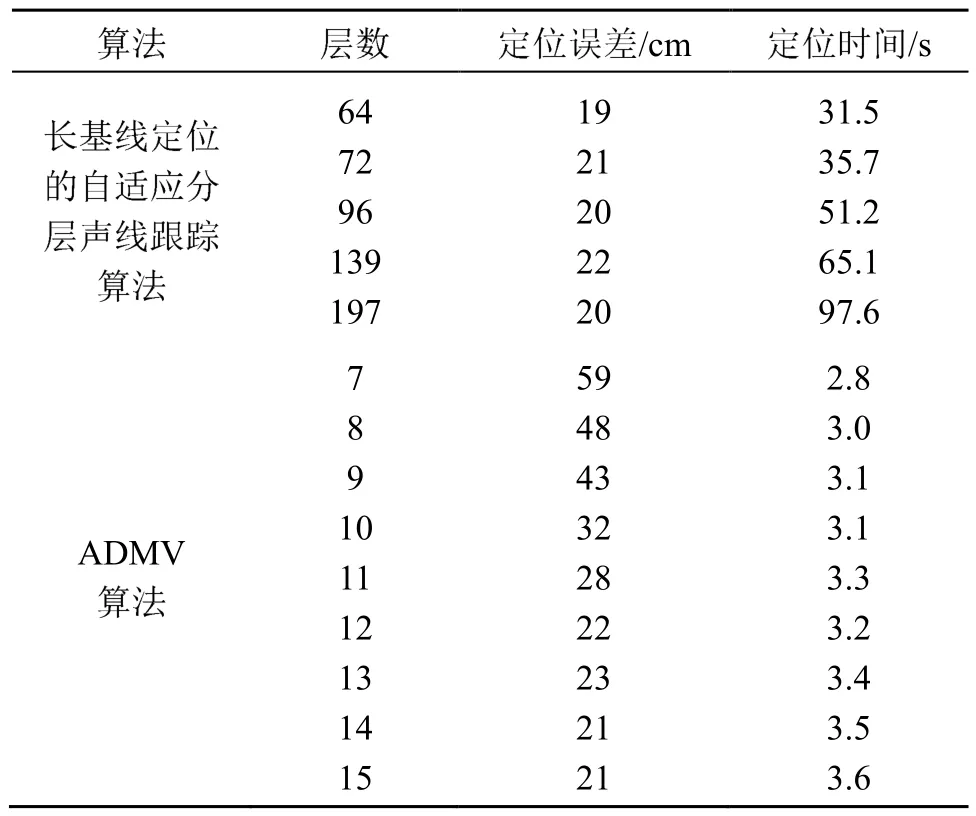
表2 两种算法定位时间对比Table 2 Comparison of positioning time between the two algorithms

3.4 不同数据集的对比

以上实验选取的数据集均来自“2010年南海海洋断面科学考察 CTD温盐观测数据集”，为了验证ADMV算法的普适性，另在“2011年南海海洋断面科学考察CTD温盐观测数据集”和“2012年南海海洋断面科学考察CTD温盐观测数据集”共3个数据集中选取 3个数据进行对比，分别命名为SVP1、SVP2和 SVP3，结果如图 7所示。由图 7可知，SVP3的定位误差随分层数的增加而降低，由于SVP3变化复杂，在分层较少时与原声速剖面差异较大，导致定位误差相对较大。随着层数的增加，误差趋于稳定。SVP1和SVP2的定位误差中间有小幅度的波动。这是因为根据等效声速剖面思想，不同声速剖面定位距离只与声速剖面的坐标轴围成面积和初始掠射角有关。重构声速剖面与坐标轴围成的面积与原始声速剖面与坐标轴围成的面积越接近，定位精度越高。不同分层与坐标轴围成的面积有所差异，但总体上定位误差随分层数的增加而降低。因此，ADMV算法具有一定的普适性，具有一定的工程应用价值。

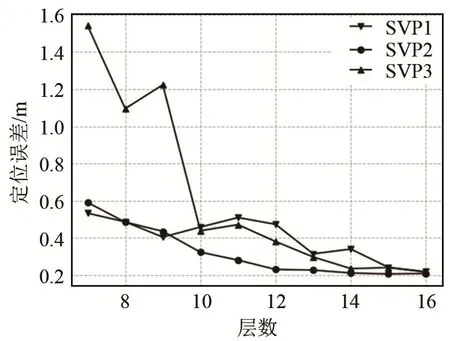
图7 不同数据集声速剖面分层数与定位误差的关系Fig.7 Relationships between the number of the sound velocity profile layering and the positioning error obtained from different data sets

4 结 论

本文针对水声定位系统中如何平衡声线跟踪计算效率与定位精度的问题，提出的 ADMV算法能根据声速在有限范围内线性变化的特点，采用实测的声速数据，通过分析阈值与层数以及定位精度的关系，找出符合条件的最佳阈值。在此基础上，通过全局搜索、迭代分层，尽可能地保留了原始声速剖面形态弯曲的特点。ADMV算法在原理上与常梯度跟踪算法思想更加契合，因而可以更好地重构原始声速剖面，在提高定位精度的同时显著提高了定位效率，并且该过程不需要人工干预，实现了自动化搜索分层与定位。