参量阵声源波束宽度影响因素分析

陈晶晶，邹彬彬，郭英歌

(中国科学院声学研究所东海研究站，上海201815)

参量阵声源波束宽度影响因素分析

陈晶晶，邹彬彬，郭英歌

(中国科学院声学研究所东海研究站，上海201815)

摘要：波束宽度是衡量参量阵声呐性能的重要技术指标之一，在设计时应该对其正确掌握，以保证整机性能.文章以圆形活塞换能器形成的参量阵声场为例，利用维斯特维尔特(Westervelt)理论和 Khokhlov-Zabolotskaya-Kuznetsov(KZK)方程分别计算了参量阵声场波束宽度，通过试验验证了KZK数值计算用于分析波束宽度的准确性及对远近场的适应性，并指出利用Westervelt理论计算参量阵声源波束宽度的不足。然后通过仿真，分别分析了频率、吸收系数、阵长与参量阵波束宽度间的关系，并从物理意义上解释了阵长对参量阵声场波束宽度的影响。

关键词：参量阵；波束宽度；Westervelt理论；KZK方程

中图分类号：TB566

文献标识码：A

文章编号：1000-3630(2020)-04-0400-06

收稿日期:2019-05-13;修回日期:2019-06-16

基金项目:中国科学院声学研究所率先计划项目(SXJH201610)、中国科学院声学研究所青年英才项目(QNYC201827)

作者简介:陈晶晶(1983－)， 女， 广西柳州人， 博士， 副研究员， 研究方向为非线性声学理论与应用。

通讯作者:陈晶晶， E-mail: cjj@mail.ioa.ac.cn

引用格式：陈晶晶， 邹彬彬， 郭英歌. 参量阵声源波束宽度影响因素分析[J]. 声学技术， 2020， 39(4): 400-405. [CHEN Jingjing， ZOU Binbin， GUO Yingge. Analysis of influencing factors on beam width of parametric acoustic array source[J]. Technical Acoustics， 39(4): 400-405.] DOI:10.16300/j.cnki.1000-3630.2020.04.003

Analysis of influencing factors on beam width of parametric acoustic array source

CHEN Jingjing， ZOU Binbin， GUO Yingge
(Shanghai Acoustic Laboratory，Chinese Academy of Science，Shanghai201815，China)

Abstract:Beam width is one of important technical indexes to measure the performance of parametric acoustic array(PAA). The PAA's beam width should be calculated correctly in designing to ensure the performance of whole system.Taking the PAA formed by a circular piston transducer as an example， the Westervelt theory and the Khokhlov-Zabolotskaya-Kuznetsov (KZK) equation are used to calculate the PAA's beam width respectively. The accuracy of the numerical calculation of KZK equation in analyzing beam-width and its adaptability to far and near fields is verified by experimental results. The shortcoming of the Westervelt's formula for beam width calculation is indicated.By simulation， the relationships between the PAA's beam width and the frequency， absorption and array length are analyzed， and the influence of PAA's length on its beam width is explained in the physical sense.

Key words:parametric acoustic array (PAA); beam width; Westervelt theory; KZK equation

0 引 言

在使用声呐设备进行探测时，声场的波束宽度是一个重要的指标，影响探测目标的分辨率[1]。参量阵声呐由于其易于获得高指向性、几乎无旁瓣的低频声场而被广泛关注并使用在各种探测领域[2-4]。目前常用于估算参量阵(Parametric Acoustic Array,PAA)波束宽度的公式是根据维斯特维尔特(Westervelt)理论提出的[5]。参量阵是一个累积阵，它的形成需要一定的传播距离，而在水声探测的应用中，这个距离一般会很大，例如，对于由300 kHz的原频完全形成30 kHz的差频声场，这个距离至少需要20 m左右(即在20 m以外的距离测量差频声源级不再变化)[6]。在水声探测领域，如果原频更低，介质对声波的吸收更小，则需要更远的距离。所以在实验室测量参量阵的远场指向性比较困难，在这种情况下无法验证估算公式计算结果的有效性。另外由于形成参量阵差频声场的距离较远，很多情况下探测目标所处的位置在阵长范围以内，把这个距离范围认为是参量阵声场的近场，对于这种近场问题的分析，Westervelt理论是不适用的。下文将用数值计算结果与 Westervelt理论估算结果进行对比，并通过实验验证，总结出参量阵波束宽度的一些变化规律并给出相应的物理解释。

1 波束宽度计算

波束宽度决定探测目标的横向分辨率。参量阵声场是两列不同频率的声波同方向传播时，由共同作用所生成的声散射声同相叠加形成的，因此参量阵声场的指向性是由原频波声场继承而来。本文中用于描述波束宽度的物理量是半功率束宽：即两个半功率点间的夹角也即功率下降 3 dB的两个场点间的夹角，所以又称为-3 dB束宽。为便于计算分析，本文将以圆形活塞换能器生成的参量阵声场为例，对于圆形活塞换能器，其原频声场的远场-3 dB波束宽度的计算公式为

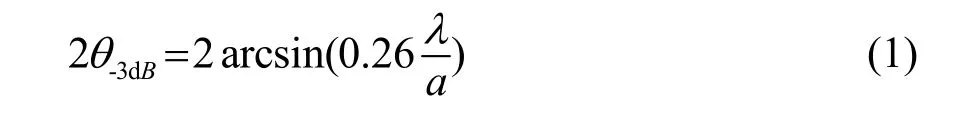
式中：λ为发射声波波长；a为换能器辐射面半径。

1.1 Westervelt理论

Westervelt于上世纪六十年代提出参量阵理论。Westervelt假设介质为理想流体、不考虑两个原频波的波束扩散(简称两原频波为标准准直束)；同时假设原频波和差频波以小振幅波进行传播，不考虑差频波的衰减，忽略非线性吸收。根据这些假设条件对莱特希尔(Lighthill)关于任意流体运动的严格方程取二级近似，推导出Westervelt非线性方程[7]：

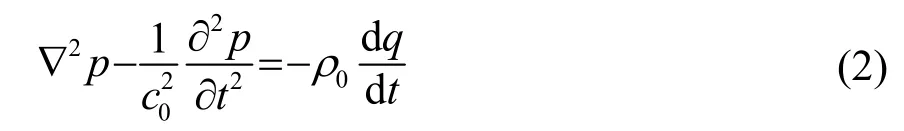
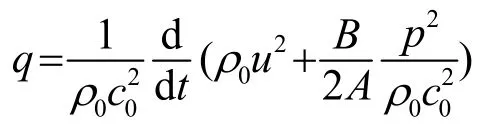
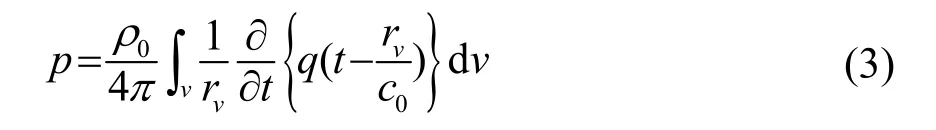
式中：rv为场中观察点到微元体积dv的距离，再根据远场近似，式(3)可以表示为

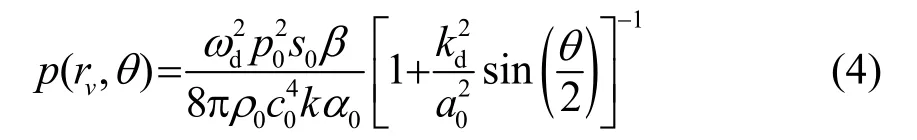
式中：脚标“d”表示的是该物理量对应的是差频：ωd表示形成的差频信号的角频率，kd表示差频信号的波数；k表示原频波的波数，p0为原频波的声压振幅(假设两列原频波的声压振幅一样)；s0为换能器辐射面的面积，a0为换能器辐射面半径；β=1+A/2B，表示介质非线性系数；ρ0为介质密度，c0为介质中小信号的声速，α0为两原频波的小振幅平均吸收系数。根据式(4)，可以得到-3 dB束宽为

根据前文介绍的Westervelt理论的基本假设可知，该理论只适用于阵长在瑞利距离以内(对于圆形活塞换能器，瑞利距离以内满足准直束的假设)以及场点在远场的情况，即式(5)只适用于文献[8]中的吸收限制阵，而对于扩散限制阵，则会使用两原频波指向性图的乘积来求波束宽度。为了克服 Westervelt理论存在的问题，Berktay对Westervelt理论加以修正[9]，经过修正后的波束宽度计算公式为

其中，分别为两列原频波以及差频波的吸收系数α称为等效吸收系数。式(6)也是目前参量阵声呐在工程设计时常用的束宽估计公式，但正如前面提到的该公式是针对于远场的估算。对于近场问题，则有学者通过对式(3)的数值计算来解决[10]。这些修正或计算仍以Westervelt理论为基础。

1.2 KZK方程

1.1 节所提到的波束宽度的计算都是基于Westervelt理论。Khokhlov-Zabolotskaya- Kuznetsov(KZK)方程是上世纪80年代提出的，对Westervelt方程做抛物线近似可推导出 KZK方程。正是由于做了抛物线近似，使得 KZK方程摆脱了准直束的假设限制，但是抛物线近似是一个近轴近似，所以使得 KZK方程描述的非线性超声场又限制在了轴旁(一般取轴附近±20°)，对于大多数探测应用来说还是比较宽松的。KZK方程可写为

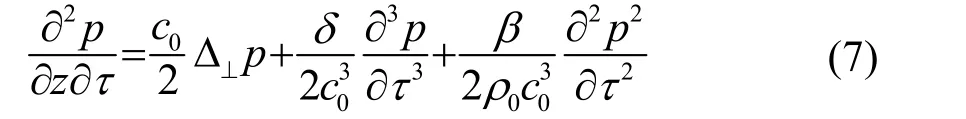
式中：p为声压，为延迟时间，δ是声散射度，Δ⊥是横向拉普拉斯算子，介质的声吸收系数，即粘滞和热传导耗散所引起的声衰减系数与声波频率的平方成正比。式(7)等号右边第一项描述声波的衍射效应，第二项描述声波的吸收效应，第三项描述声波传播方向的非线性效应。该方程难以求得精确解析解，常用数值解法求解。

KZK方程的数值计算方法可分为时域和频域两种。两种方法各有其优缺点，在选择了合适的计算参数后，使用这两种方法计算出来的参量阵声场是一致的。考虑到实验使用的发射信号为脉冲(burst)信号，使用时域方法更为合适，而圆形活塞换能器辐射声场是轴对称的，可用二维时域有限差分算法(Texas code)[11]来计算参量阵声场。时域方法计算得到的声场是一个总声场，会包含由于非线性效应产生的各种频率成分，要分析参量阵声场就需要从总声场中提取出差频成分。在本文中对计算得到的结果再进行快速傅里叶变换(Fast Fourier Transform, FFT)，然后提取出差频频率幅度用以分析参量阵束宽。由于KZK方程摆脱了准直束假设，综合考虑了非线性、吸收、衍射等作用的影响，所以除去数值计算的计算误差，使用该方法得到的波束宽度比式(6)的计算结果更准确。

2 实验对比

为了验证以上两种方法对声束宽度计算结果的准确性，进行了相关的验证性实验。为了验证KZK方程对近场声场的适应性，设计了一个频率为300 kHz的换能器，发射的瞬时峰峰值功率为3 000 W。频率为 300 kHz的声波在清水中的吸收系数为 23.4 dB·km-1，分别调制形成 10、20 kHz和40 kHz的参量阵差频声场，在这种情况下在清水中的阵长约为 20 m左右，这个距离远超出了实验水池的距离。在6 m处测量分别测量了300 kHz原频波和差频波的波束宽度。实验结果与 KZK方程的数值计算结果表1所示。

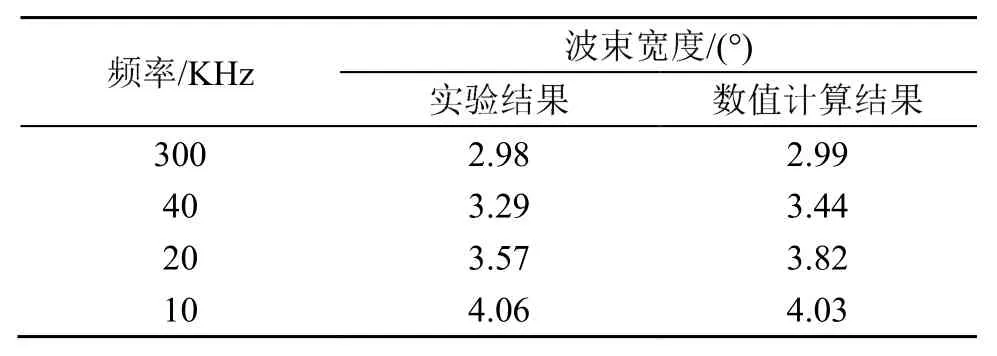
表1 参量阵近场波束宽度测试值与数值结算结果对比Table 1 The measured and caculated near-field beam widths of parametric acoustic array

由表1可见，采用KZK方程数值计算的方法能较为准确地估算出参量阵近场的波束宽度。为了能够验证参量阵远场的情况，把原频波的频率提高到1 MHz，发射瞬时峰峰值功率为242 W，1 MHz声波在清水中的吸收系数取 240 dB·km-1，生成差频频率为80 kHz的参量阵声场，此时的参量阵的阵长约为1.5 m，在3.5 m的距离测量差频声场指向性图。测量结果和数值计算结果如图1所示。

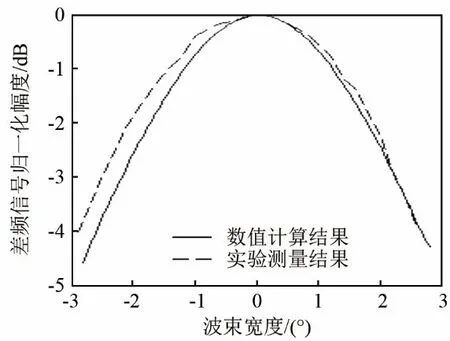
图1 参量阵远场波束宽度的数值计算结果与实验测量结果对比图Fig.1 Comparison between calculated and tested far-field beam widths of parametric array

该情况下数值计算得到的波束宽度为 4.43°，实验测量结果为4.67°，而式(6)的计算结果为6.38°。由以上的试验对比结果可以看出，通过 KZK方程的数值计算得到的参量阵声场远场波束宽度与测试结果更为接近，而式(6)的计算结果与测试结果相差较大。

3 仿真分析

3.1 频率下降比与波束宽度间的关系

频率下降比表示为f0/fd，即原频频率与差频频率之比。从式(6)可以看出直接影响波束宽度的两个物理量分别是原频波的吸收系数和差频波的波数，波数反映的是声波的频率。因此，差频频率越高，则波束宽度越小。在原频波的频率固定不变的情况下，根据Berktay的包络自解调理论，考察不同的差频对应的波束宽度的变化规律。表2～4分别是用两种方法计算的 200 kHz和300 kHz、1 MHz原频形成不同差频声场的波束宽度的结果。

在这3个仿真中，原频波对应的波束宽度分别为3.26°、2.98°和3.19°。从表2～4中的数据可知，无论是用数值计算还是用式(6)估算，参量阵声场的波束宽度都会随着差频频率的增大而减小，但数值计算的结果和公式估算结果在某些频率上相差较大。为分析公式估算与数值计算间的差值的规律，接下来将从频率下降比的角度进一步分析。将表2～4的数据表示为波束宽度与频率下降比之间的变化关系，如图2～4所示。

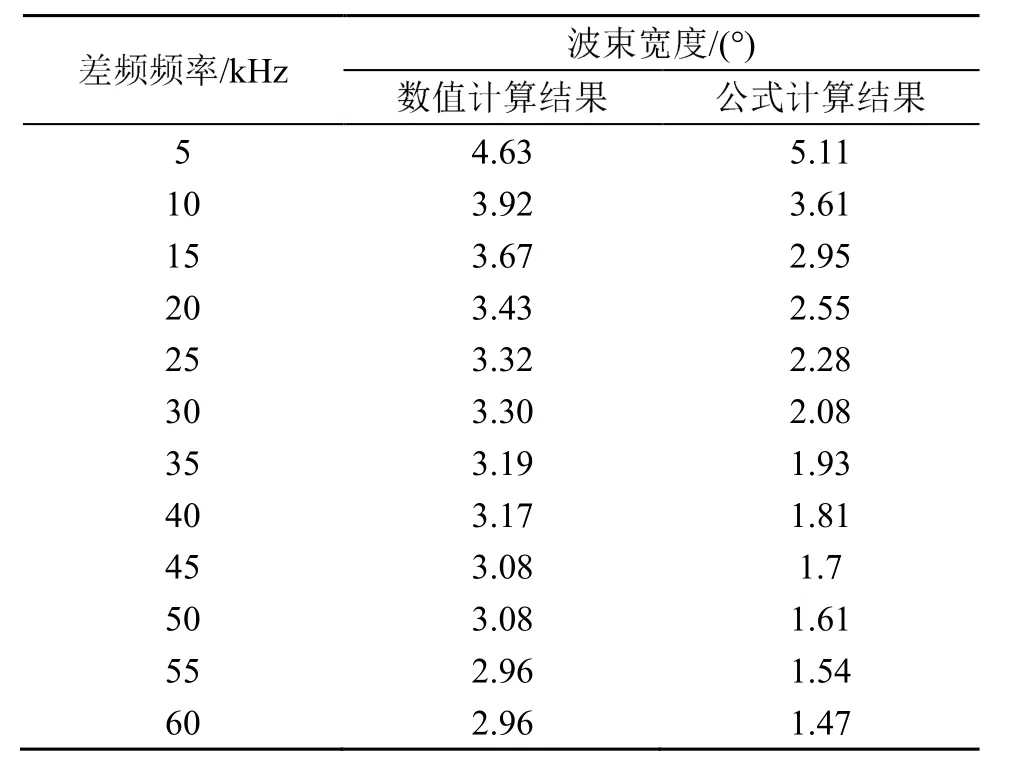
表2 原频200 kHz时不同差频生成参量阵声场的波束宽度对比Table 2 Comparison of PAA's beam-widths generated by different difference frequencies at the primary frequency of 200 kHz

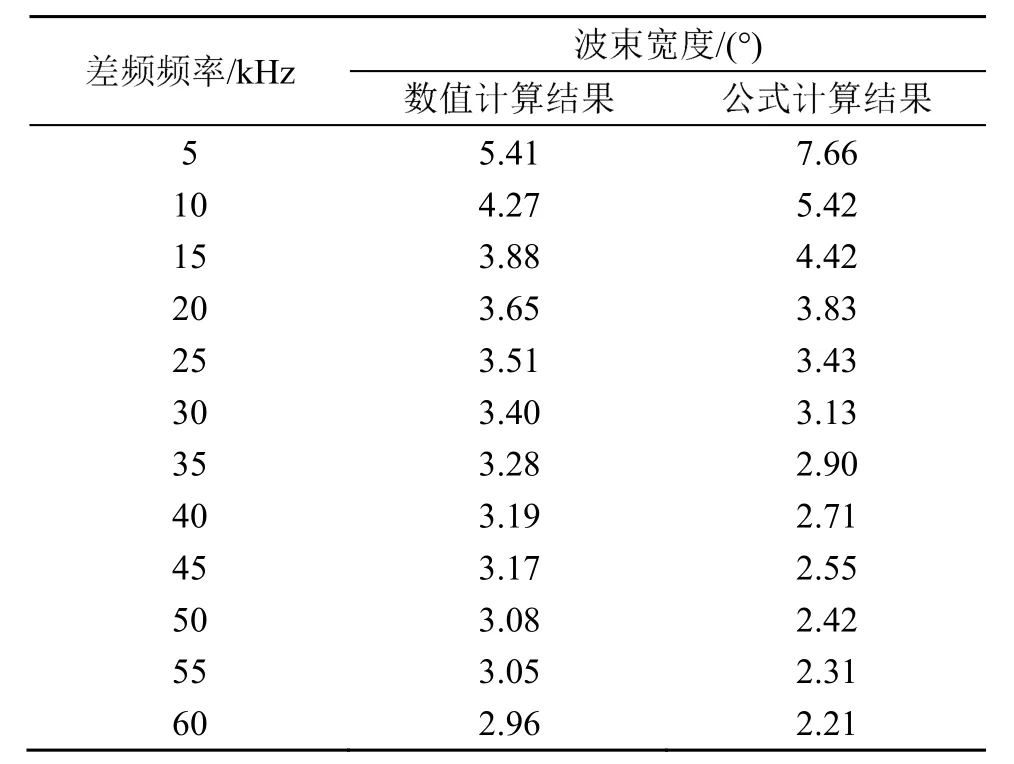
表3 原频300 kHz时不同差频生成参量阵声场的波束宽度对比Table 3 Comparison of PAA's beam-widths generated by different difference frequencies at the primary frequency of 300 kHz

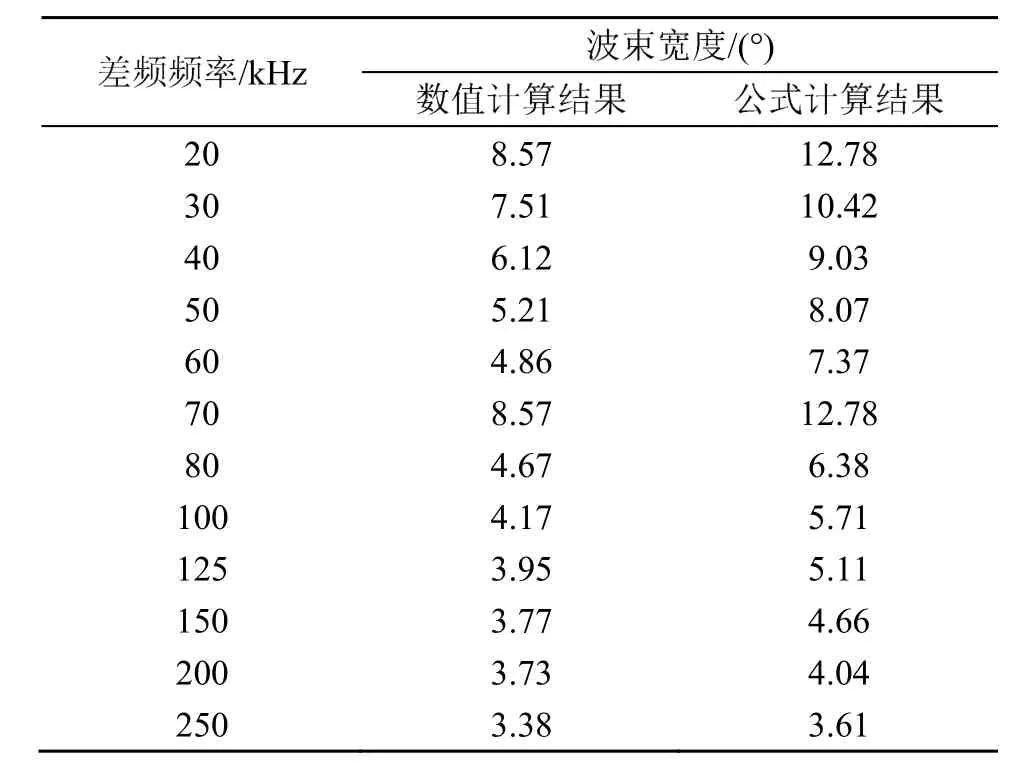
表4 原频1 MHz时不同差频生成参量阵声场的波束宽度对比Table 4 Comparison of PAA's beam-widths generated by different difference frequencies at the primary frequency of 1 MHz

从图 2～4可以看出，在每一组数据中，总有一个位置附近的数值计算结果与公式估计结果比较接近，而这个位置会随着原频的升高向频率下降比低的方向移动。从数值计算结果的曲线可看出，频率下降比与角度的关系基本符合一个线性的关系，对以上各计算结果进行线性拟合，把线性拟合中的截距设置为原频的波束宽度，这样设置的理由是在极端的情况下即差频等于原频时，差频对应的波束宽度应该与原频是一致的，拟合得到的公式分别如图 2～4中所示。进一步分析拟合公式可看出，随着原频的升高，斜率也在不断的变大，从这3组数据结果表现出来的规律是，原频升高 100 kHz，则斜率增大约0.01。虽然斜率变化的规律只是由这3组数据做出的一个粗略的分析，但是可以在参量阵系统设计波束宽度指标提供指导。

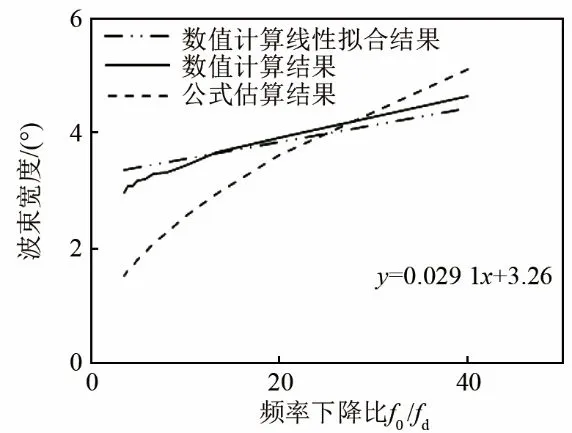
图2 原频200 kHz时参量阵声场波束宽度随频率下降比的变化关系图Fig.2 Variations of PAA's beam width with frequency drop ratio at the primary frequency of 200 kHz

图3 原频300 kHz原频时参量阵声场波束宽度随频率下降比的变化关系图Fig.3 Variations of PAA's beam width with frequency drop ratio at the primary frequency of 300 kHz

图4 原频1 MHz原频时参量阵声场波束宽度随频率下降比的变化关系图Fig.4 Variations of PAA's beam width with frequency drop ratio at the primary frequency of 1 MHz

3.2 吸收系数与波束宽度间的关系

式(6)中两个原频波的小振幅平均吸收系数α1、α2也是影响参量阵波束宽度的因素之一。固定原频波和差频波的频率为1 MHz和100 kHz，取清水中不同温度对应的声吸收系数做仿真，结果如图5所示。

从图5可以看出，波束宽度随着吸收系数的增大而增大。根据式(6)得到的估算值满足的是一个幂函数的关系，而数值计算结果更接近线性函数关系。

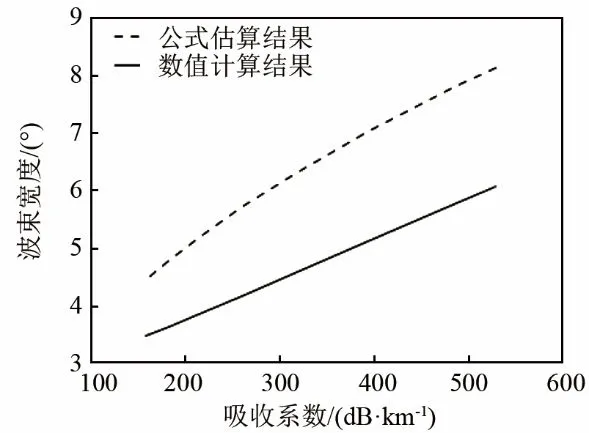
图5 固定原频和差频频率情况下参量阵波束宽度与吸收系数关系图Fig.5 Relationship between PAA's beam width and absorption coefficient for fixed primary frequency and diffrence frequency

3.3 阵长与波束宽度间的关系

3.1 、3.2节是从式(6)中的两个变量分别来探讨差频频率与衰减系数对参量阵声场波束宽度的影响。从物理意义上，能够更好地解释影响参量阵声场束宽的变化规律的变量是阵长。参量阵实际上可视为由无数个虚源组成的体积阵。一些文献里会根据源函数的不同，把这种体积阵简化为不同的模型，例如针对Westervelt理论的准直束假设把体积阵简化为圆柱模型[12-13]；考虑球面波的扩散效应后把体积阵简化为圆台模型[13]。无论简化为何种模型，阵的尺寸都是决定声场指向性或者说是波束宽度的一个重要因素，一般是尺寸越大即阵长越长，指向性越尖锐[1]。

参量阵的阵长可理解为两列原频波相互作用可以忽略的距离。这个距离受扩散、非线性以及声吸收的共同影响，其中声吸收的影响最大。因此一般情况下，阵长的估算公式为[10]

其中：α的定义与式(6)一致。从式(8)可以看出，原频波吸收系数越大，阵长越短；而差频波吸收系数越大，阵长越长。结合3.1和3.2节的仿真结果可知：对于固定原频的情况下，差频越大对应的吸收系数越大，则波束宽度越小；而对于固定频率的情况，在不同温度下原频和差频的吸收系数都有变化，但是由于原频波的吸收系数一般高于差频波的吸收系数2个量级，所以在这种情况下波束宽度仍表现出随原频吸收系数增大而增大的趋势。

比较表1和表2中对应差频频率的波束宽度结果，表1的结果比表2中的大，这是因为表1中计算的是截断情况，参量阵还没有达到阵长距离，还没有完全形成差频声场。另外，关于式(6)的计算结果与数值计算结果相差较大的情况，也可从阵长方面加以解释。前面已经介绍，式(6)的推导是以准直束为基础的，对于圆形活塞换能器，其有一个隐含的假设即瑞利距离为参量阵阵长，而这种限制在很多情况下与实际情况并不一致，所以得到的结果也不一致。

由于 KZK方程目前没有精确解析解，所以以上关于阵长与参量阵声场波束宽度间的关系，只能进行一些定性的分析，要定量分析两者间的关系，还需要进一步的理论研究以及更多的仿真结果。

4 结 论

波束宽度是参量阵声呐一个重要的设计指标，关乎设备对目标的分辨率，因此在设计参量阵声呐时，需要对所使用的参量阵声场的波束宽度进行较准确的估算。目前常用的参量阵声场波束宽度的估算公式的适用情况有限，在很多情况下计算结果误差较大。KZK方程能准确地描述非线性超声场，但目前只能通过数值计算得到其声场解。通过 KZK方程数值计算得到的波束宽度结果与实验结果吻合，而且不受近远场的限制以及参量阵模型的限制。本文根据一系列数值计算结果与公式结果的仿真对比，定性地分析了波束宽度受频率下降比和吸收系数影响的规律，并通过阵长的概念对这些规律做出了物理解释。