基于光流法的固体内部声传播方向测量

匡鹿婷，宋 波，毛 捷，廉国选

(1. 中国科学院声学研究所声场声信息国家重点实验室，北京100190；2. 中国科学院大学，北京100049)

0 引 言

光弹法是利用光弹材料的暂时双折射现象，来分析应力问题的一种方法。文献[1]中提到，Brewster于1815年首次发现了光弹现象。上世纪30年代初，Coker和Filon于剑桥大学出版了《论光弹》，为光弹现象的物理机制奠定了基础。40年代仪器设备的改进和新型材料的使用，解决了一系列的弹性力学难题，使光弹法成为比较完善的技术[1]。中国科学院声学研究所应崇福院士等于上世纪80年代搭建了一套国际领先的动态激光光弹设备[2-6]，国内最早的 LED光源动态光弹系统由清华大学物理系开发[7]，随后中北大学[8]，南昌航空大学[9-10]等都使用此类设备进行教学科研工作，国外也有同类型设备在售[11-12]。

动态光弹法是目前仅有的能够全场、直接、非入侵地观测透明固体内部超声应力分布的光学实验方法。与解析理论和数值方法相比，动态光弹成像法能够提供更为准确和接近实际物理模型的实验结果。现有的利用光弹设备进行固体中声波传播方向的判定方法多为直接观察的定性判断，无法实现对声传播方向的准确定量观测。然而，光弹法作为能够唯一观测固体内部声场的实验方法，将其由定性观察改进为定量判断的仪器，具有重要的科学意义。本文采用光流法分析动态光弹图像，对声波传播进行准确的追踪，通过计算声传播区域的光流矢量值，定量计算超声传播的方向。

1 理论分析

1.1 光弹系统基本原理

当固体内部存在应力时，由于双折射效应，应力区将使入射光改变偏振方向，部分出射光将通过检偏器而被相机接收，形成光弹图像，图像中测点的亮度与该点应力的大小和方向有关。假设入射光强度为I0，不计衰减，则透射光强I为

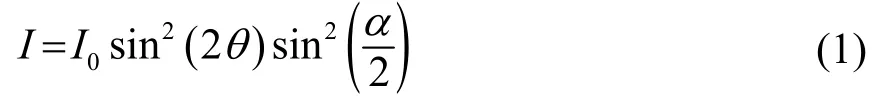
式中，θ是任一主应力σ1或σ2与任一偏振轴的夹角，可看出当偏振轴与主应力方向重合时，透射光强为0，达到消光状态。α为入射偏振光双折射后的相位差，表达式为

其中：η为应力光弹系数，是样品材料的特性。l是样品的长度[13]。

1.2 斯涅尔定律

实验中采用不同角度的楔块改变声波入射角，所用楔块与实验样品为两种不同的介质，声波在楔块与样品界面会发生折射现象，根据斯涅尔定律，可以获得声波在样品中的传播角度：

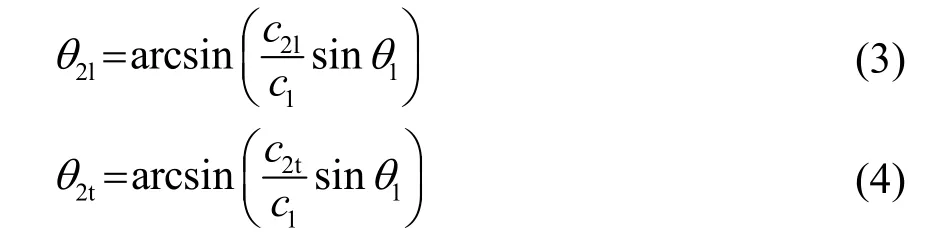
其中，θ1和θ2l、θ2t分别为入射波和折射波与法线的夹角，即声波在楔块和样品中传播的角度[14]，c1为楔块中的纵波声速，c2l、c2t分别为样品中纵波和横波的传播速度。当楔块角度小于第一临界角时，样品中纵波和横波同时存在；当楔块角度大于第一临界角时，样品中只有横波存在。

1.3 光流法原理

光流法[15]是在图像序列或者视频中，根据帧与帧之间的相关性以及像素在时间域上的变化来得到当前帧与下一帧之间存在的对应关系，进而计算出相邻帧之间物体运动信息的一种方法。本文首次将光流法用于动态光弹图像序列中，使用Farneback金字塔算法[16]计算光弹图像的光流矢量值，光流结果的统计值很好地反映了声的传播方向。

1.3.1 基本原理

光流法选取图像序列的前后两帧图像基于两种假设进行处理，即假设亮度恒定不变和时间连续。在相邻帧图像之间，假设图像上任意一点的像素值为I(x,y,t)，经过时间Δt，在下一帧图像中该点在水平、垂直方向分别位移Δx、Δy，对应的像素值为I(x+ Δx,y+ Δy,t+ Δt)。根据光强恒定假设，并忽略二阶无穷小，可得：

其中，Ix、Iy、It均可由实验数据获得，u、v即为要求的光流矢量。

1.3.2 Farneback算法原理

式(6)中的光流等式为超定方程，还需其他的约束方程。Farneback算法的核心思想是光流的局部平滑约束准则。该算法将图像近似为二维信号的函数，利用二次多项式对图像进行建模[17]，可得表达式为

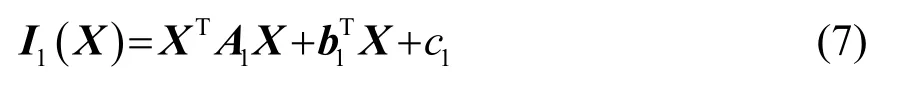
其中，二维坐标点X= (x,y)T为因变量，c为常数。

1对上式进行系数化之后，等式右侧可写为

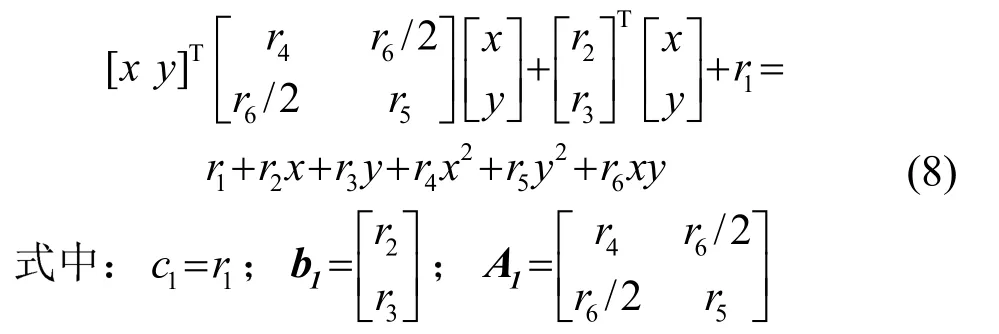
通过在第一帧图像的基础上增加全局位移d来构建下一帧图像信号，得到下一帧的图像表达式为

由光流算法的基本约束条件为一恒定像素值的假设，可得：

可得位移计算公式：

由上式计算结果可得到每个像素点在水平方向和竖直方向的偏移量，对应式(6)中的u,v。光流法得到的光流场为d(x,y)，其中dx,i,j、dy,i,j为光流的水平分量和垂直分量，进而可以由下式求得光流矢量的角度信息[18]：

Farneback光流法中引入了金字塔算法，其目的是为了解决上述方法只适合小位移的运动情况。金字塔算法的主要思想是构建一个图像序列的金字塔模型，利用采样技术逐级缩小图像，可将相邻帧之间图像的大尺度运动缩小，这样仍然可以采用上述的光流方法[19]。

2 实验及结果分析

2.1 实验平台及条件

为观测超声传播方向，我们搭建了如图1所示的动态激光光弹系统。该系统由光学平台、激光器、凹透镜、凸透镜、起偏器、样品(K9玻璃)、检偏器、相机和同步延时系统组成。其中，光学实验平台有很好的抗振动干扰能力。实验平台左端的扩束透镜焦点和准直透镜焦点重合，将激光扩束为直径120 mm的平行光；右端的会聚透镜将平行光束汇集，在相机处聚焦。图1中的样品为声场的载体，起偏器和检偏器可调节入射光场的偏振状态，进而实现明场或暗场成像。同步延时系统用来调节两路相对延时，一路触发超声发射电路，另一路触发激光器，再通过相机进行拍摄，从而实现对超声在固体中的传播以及散射过程的观测[3]。可通过计算机获取超声传播图像，用以做光流计算。

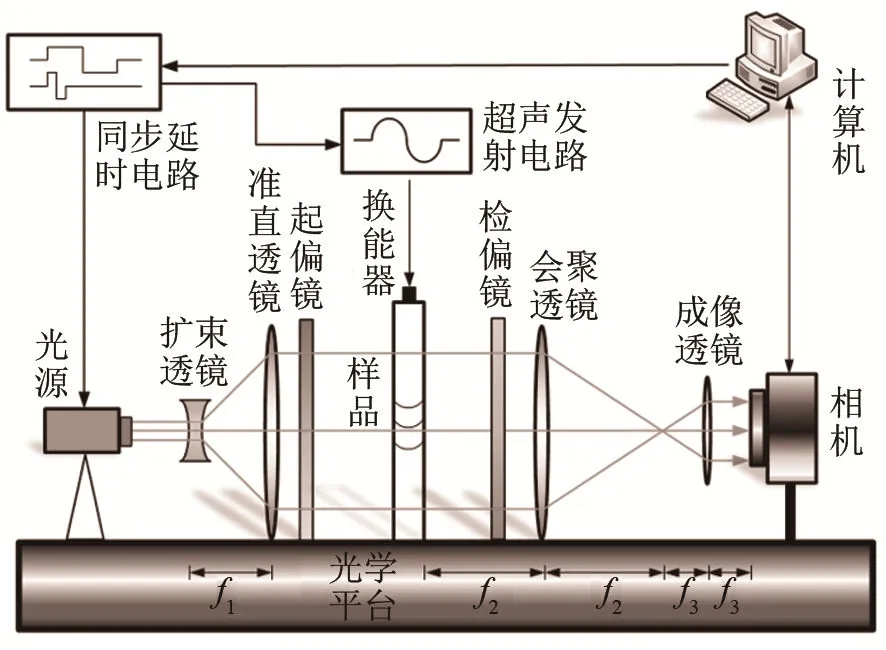
图1 动态激光光弹系统的实验平台Fig.1 Experimental platform of dynamic laser photoelastic system

通过以下条件使实验满足光流法的前提假设：

(1) 实验样品材料选用经过精退火处理的 K9光学玻璃，样品长、宽均为120 mm，厚度为20 mm，超声在K9玻璃中衰减较小，能量基本不变，可保证超声波成像亮度基本稳定。

(2) 采集图像时，间隔时间设置为0.22 µs，以保证时间连续条件。

(3) 调整激光光源强度，控制图像灰度化后最大亮度位于饱和值的35%～80%区间内。

(4) 采集图像时声波位置需避开探头的近场区域，以保证声场能量的均匀变化。

2.2 实验结果与分析

实验中，本课题组自制的中心频率为2.5 MHz的圆盘型纵波压电换能器在窄脉冲作用下产生超声波。首先，通过楔块耦合的方法获得了不同传播方向的超声平面波，其传播方向的实际角度值可根据斯涅尔定律计算得到。然后，采用光流法对超声传播方向进行了计算，并将计算结果与实际角度值进行了对比验证。最后，在无楔块的情况下重复做了8组实验来验证方法的重复性。

2.2.1 预处理及结果统计方法

在实验过程中，通过控制图像采集时间间隔来减少帧与帧之间像素的衰减值，并且进行光流计算之前对图像进行归一化预处理，进一步解决图像序列中的像素亮度衰减和梯度不明显的问题，归一化公式为

式中：I为每点的像素值，I′为归一化之后的每点像素值，Imin为图像中像素点亮度的最小值，Imax为像素亮度的最大值。由于两帧图像的采集间隔时间较短，图像像素亮度值衰减较小，归一化方法不会在像素级别改变声波边缘的扩散情况。

根据式(14)可得到光流法计算出的声传播角度，由于声波的能量主要集中于中心较亮区域，选取亮度值大于 0.75倍最大亮度值的集合为计算区域，用其光流矢量平均角度来表征声传播方向，即：

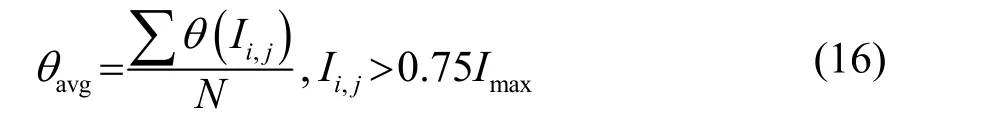
式中，θavg为光流矢量角度平均值，即声传播方向。N为区域内满足条件像素点总个数，θ(Ii,j)为区域内点(i,j)位置的矢量角度值。实验中采用区域角度平均的统计方法可减小局部箭头偏差带来的误差。

2.2.2 光弹图像采集

实验中所使用的楔块为聚苯乙烯材料，纵波在其中的传播速度为 2 300 m·s-1，在 K9玻璃中的纵波声速为 6 000 m·s-1，横波声速为 3 600 m·s-1。经计算可知楔块与K9玻璃两种介质交界面处的第一临界角为22.5°。实验采集了6组光流图像序列，第一组为无楔块情况下，声波垂直入射进玻璃中的图像。其余图像对应楔块的角度分别为：12.34°、17.40°、22.89°、27.08°、31.66°。采集的 6 组光弹图像如图2所示。

图2 不同角度楔块获取的光弹图像Fig.2 Photoelastic images for the wedge at different angles

2.2.3 实验结果与分析

图像归一化处理之后进行光流计算，光流场图如图3所示，图像中光流矢量值以箭头的形式每隔10个像素点进行显示。其中3(a)为纵波光流矢量图，图3(b)和3(c)同时给出了折射纵波和横波的光流矢量图，图3(d)、3(e)和3(f)为横波光流矢量图。

图3 不同角度楔块下对应的光流场图Fig.3 Corresponding optical flow field diagrams for the wedge at different angles

根据式(16)和式(3)，可分别通过光流法和斯涅尔定律得到在不同角度楔块耦合下的实验和理论计算获得的声传播角度，实验数据如表1，2所示。

实验中在无楔块的情况下连续采集8次光弹图像，并进行光流计算，实验结果如表3所示。

根据表1和表2的实验数据，可计算出实验样本和理论样本之间的相关系数为0.996 1，最大绝对误差是2.85°。由表3的数据可知，8组实验数据的平均值为1.15°，标准差为0.94°，可见该方法的可重复性较好。通过对实验数据的分析可知，误差的主要来源为随机误差，如激光光源的稳定性、系统成像的均匀性以及探头与样品的相对位置等。

表1 纵波折射角统计结果Table 1 Statistical results of the refraction angle of longitudinal wave

表2 横波折射角统计结果Table 2 Statistical results of the refraction angle of shear wave

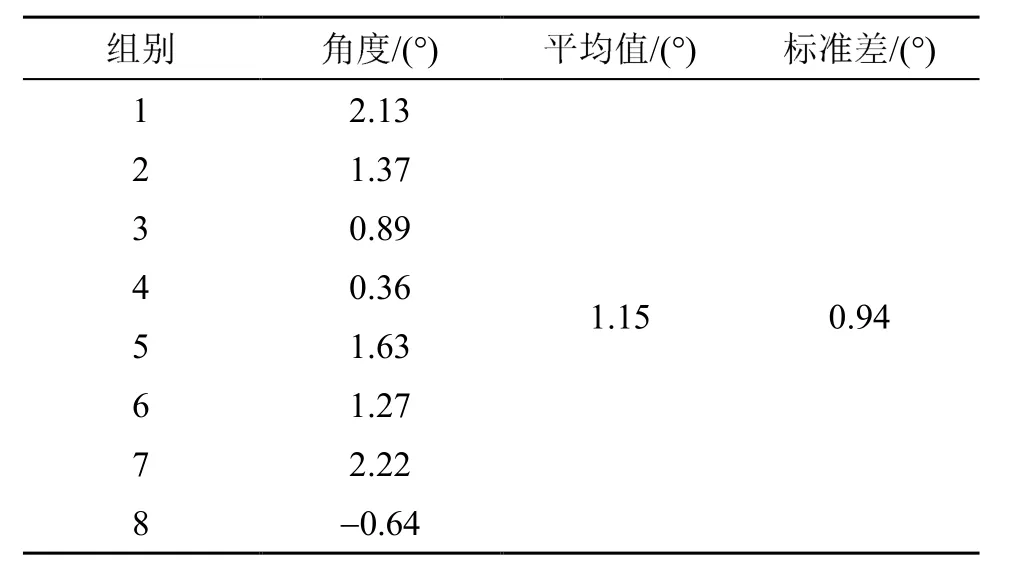
表3 声波垂直入射8次实验光流计算值Table 3 Optical flow calculation values for 8 experiments of vertical incidence of sound wave

3 结论与展望

现有的动态光弹实验设备主要是对固体内部的声场进行定性观测，对于声波的传播方向多为人眼的主观观察，不能准确地测出固体内部的声传播方向。本文采用光流法对光弹系统图像进行处理，能够快速、准确、直观地给出固体内部声场中声波的传播方向。实验结果与理论计算的最大误差为2.85°，实现了动态光弹设备对超声波传播方向的准确定量测量。该方法适用于固体内部声场清晰且图像帧间隔相对较小的情况，若散射声场过于复杂会影响帧与帧之间图像中像素亮度值的变化，从而导致光流结果的误差增大。本文结果统计中选取亮度中心区域进行均值统计，可避免局部误差对实验的影响。另外，在声波类型确定的情况下，固体内部超声波传播方向还可反映声波主应力方向，故也可用光流法计算出的声传播方向表征主应力方向。