基于多分辨率时频特征融合的声学场景分类
2020-09-15杨吉斌张雄伟郑昌艳
姚 琨,杨吉斌,张雄伟,郑昌艳,孙 蒙
(陆军工程大学,江苏南京210007)
0 引 言
智能系统要想充分利用声音信息,不仅要识别语音[1]和音乐[2]等单一的声音信号,还要充分利用周围环境中的声音信息,声学场景分类(Acoustic Scenes Classification, ASC)的目的就是利用周围环境中的声音信息对预先定义的有限场景类型进行分类。近几年,ASC已经成为声学场景和事件的分类和检测(Detection and Classification of Acoustic Scenes and Events, DCASE)挑战赛中最热门的任务之一[3-6],在智能穿戴设备的自动模式调整等方面有着广泛的应用前景。
ASC的目的是通过选择一个语义标签来描述音频流表达的声学环境,是机器学习中典型的单标签分类任务。与一般的音频分类任务类似,ASC任务的关键就在于模型设计和音频信号特征选取两个方面。
在特征选取方面,多采用音频信号的二维时频表示,时间轴以帧为单位构造长帧,频率轴为帧信号短时傅里叶变换的降维表示。其中最为典型的有梅尔频率倒谱系数(Mel-Frequency Cepstral Coefficients, MFCC)[7]、对数梅尔子带能量(Log Mel-band energies, LME)等特征。它们都是对音频信号谱包络的整体描述,同时经梅尔滤波器处理过后符合人的听觉感受,具有较好的区分度和鲁棒性。
文献[8]对场景音频信号的声谱图进行非负矩阵分解(Non-negative Matrix Factorization, NMF),输出一组激活函数。这组激活函数对基函数的贡献进行编码,从而对声学场景的属性进行建模。
在分类模型方面,由于 ASC是语音识别和音乐识别的拓展研究,在这些任务中广泛使用的模型[9-10]也被应用到ASC任务中,如隐马尔可夫模型(Hidden Markov Model, HMM)、高斯混合模型(Gaussian Mixed Model, GMM)和支持向量机(Support Vector Machine, SVM)。近年来,由于深度神经网络对非线性问题强大的表征能力,在语音和图像方面取得巨大的成功,人们开始把深度学习的方法应用到了 ASC任务中来,包括深度神经网络(Deep Neural Network, DNN)、卷积神经网络(Convolutional Neural Network, CNN)、循环神经网络(Recurrent Neural Network, RNN)等。
Eghbal-Zadeh等[11]提出了两种方案并且包揽DCASE 2016中ASC任务的前两名。第一种方案是用音频信号左声道、右声道、两声道的均值和差值4种MFCC特征分别训练身份认证矢量(Identity Vector,i-vector),最后以分类得分的均值作为结果输出。第二种方案是在第一种方案的基础上,融合以声谱图为特征的CNN网络。Zheng等[12]在对音频信号进行短时傅里叶变换时,通过改变滑动窗的宽度、FFT的点数、窗的重叠量、降维的尺度等提取不同的声谱图特征,并融合常数Q变换(Constant Q Transform, CQT)特征训练CNN模型。Han等[13]以LME为基础,从左右声道、左右声道和或差的音频中提取LME及单声道谐波和冲击响应特征等,分别训练视觉几何组(Visual Geometry Group, VGG)结构的模型,最后取所有模型分类精度的均值作为最终输出。
虽然以上方案都取得了较好的分类效果,但还存在以下几个问题:
(1) 声谱图特征的维度过高,需要以更深层的网络以及更大的数据量作为支撑,极大地耗费计算资源,且含有大量的冗余信息,类别间的区分度也不够高。
(2) 单一的低维度特征对音频信号的表征能力有限,现有的特征融合方法可解释性较差。
(3) 分类模型不具针对性,将在图像任务中表现较好的模型(如VGG等)进行简单的移植,并不能考虑到ASC任务中输入声音特征的时频结构。
为解决以上问题,本文以 CNN为基本识别模型,在时频特征基础上进行了包络/结构特征融合、适应时频结构特征的多分辨率模型设计等融合处理。模型方面,本文基于CNN模型提出一种适应声音时频结构的多分辨率卷积池化方案,并构造多分辨率卷积神经网络(Multi-resolution Convolutional Neural Network, MCNN)模型;特征选择方面,采用低级包络特征LME辅以高级结构特征NMF,在特征表征能力增强的同时,数据量及冗余信息增加较少,从而在模型和特征两方面共同完成对时频特征的融合。在DCASE2017和DCASE2018数据集上进行实验,结果验证了本文提出方案的有效性。
1 方案框架
本文采用特征提取-模型分类的实现框架。声音特征提取和模型分类系统的流程框图如图1所示。特征提取部分分为两个分支,分别提取 LME特征和NMF特征。提取NMF特征时,首先提取音频样本的声谱图特征,然后利用由所有训练集样本训练得到的字典矩阵W,对提取到的声谱图特征进行NMF,得到系数矩阵H作为NMF特征。特征融合部分,借鉴图像任务中 RGB三通道的方法,把二维的LME和NMF特征堆叠为三维特征。最后把得到的三维特征送入MCNN模型得到分类结果。实验证明,对于这两类特征,本文的融合方法要优于简单拼接和模型结果融合的方法。
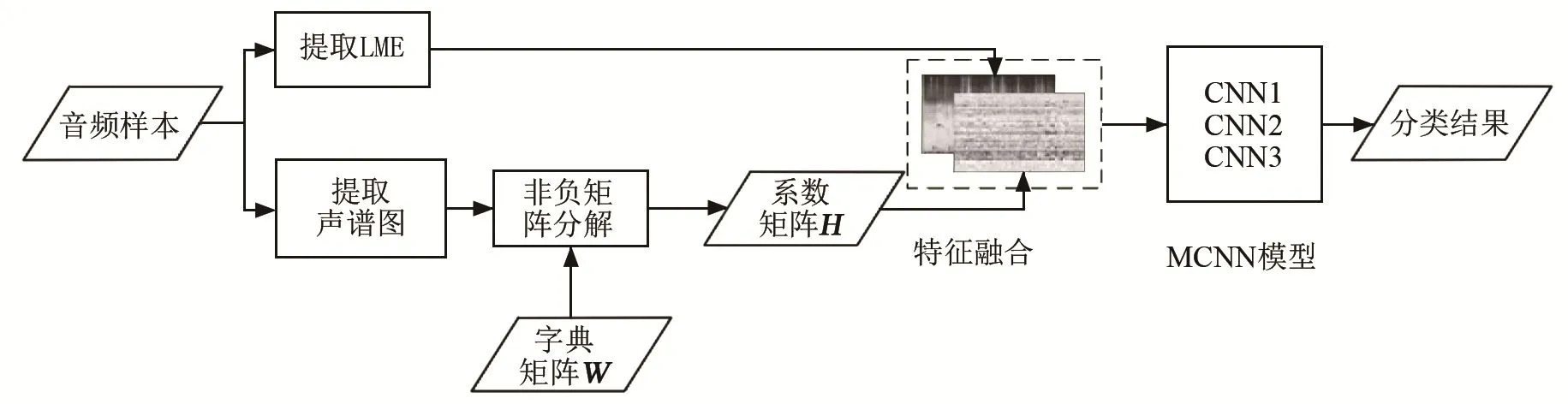
图1 声音特征提取和模型分类系统的流程框图Fig.1 Block diagram of voice feature extraction and model classification system
2 MCNN模型
2.1 适应声音时频结构的CNN框架
对声音信号进行短时处理后,其前后相邻帧的频谱分布高度相关,而频率轴上在经过后续提取手工特征时的降维处理后,彼此相对独立。针对这一特点,基于 CNN框架,提出一种适应声音时频结构的池化策略,即池化操作时只沿着时间轴进行(频率轴采样因子为1),并且在经过两次池化后,特征在时间轴上维度变为1而频率轴维度保持不变。依此方法,可以设计出适应声音时频结构的CNN模型。
图2为本文模型第二层卷积的卷积核在输入特征图上的感受野示意图,深色部分为实际特征图,白色为“补0”部分。由图2可知,CNN提取到的高级特征是由输入特征图感受野上的数据经过卷积层加权求和及池化层采样得到的,卷积核在输入特征图上感受野的范围取决于卷积核和池化窗的大小及形状。采用带状的感受野,可以更好地适应输入特征图的时频结构。

图2 时频感受野示意图Fig.2 Schematic diagram of time-frequency sensing field
2.2 MCNN
改变卷积核和池化窗的大小会影响 CNN提取到的高级特征,从而直接影响到分类结果。采用不同大小的卷积核和池化窗可以捕捉到更全面的信息,小的卷积核和池化窗对应输入特征小的感受野,从而可以捕捉到特征图上的细节信息,大的卷积核和池化窗则相反,二者互为补充。
为此,我们在 CNN中采用不同尺寸的卷积核和池化窗组合,力求同时捕捉细节和宏观信息。由于第二层卷积输出的高级特征来自于不同的子模型,每个子模型输出特征由同一输入特征图上不同大小的感受野提取得到,所以称之为多分辨率卷积神经网络(MCNN),模型结构和参数如表1所示。其中,在输入层分别采用了5×5卷积+1×5池化、7×7卷积+1×10池化、3×3卷积+1×2池化操作,在中间层分别采用了5×5卷积+1×100池化、7×7卷积+1×50池化、3×3卷积+1×250池化。这些参数都是经过组合实验优选出来的结果。
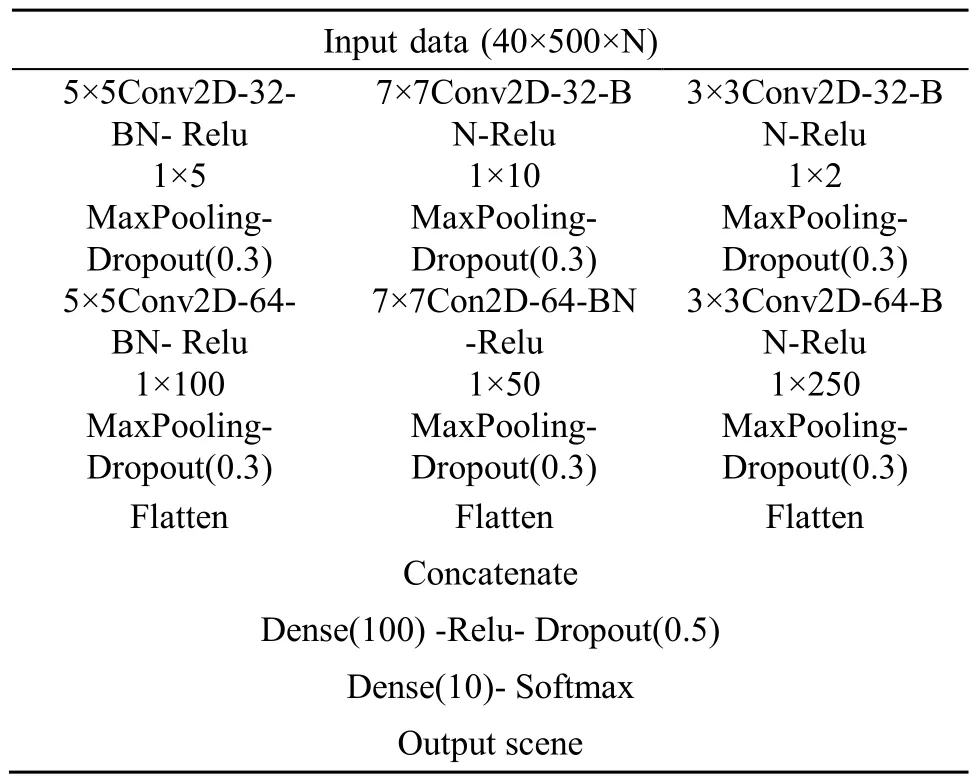
表1 MCNN模型结构Table 1 MCNN model structure
3 特征选取
LME特征能反映声谱图帧内各频带的局部统计特性,对ASC任务中的音频样本有较好的低维表征能力,在近年来的ASC任务中使用最为广泛[13-14]。因此本文对特征的研究以LME为基础,针对LME特征的不足,提出LME与NMF特征的融合思路。
3.1 LME特征
把音频信号分帧、加窗后,对每帧信号进行离散傅里叶变换,可得:
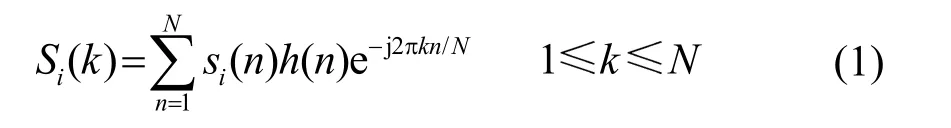
其中:si(n)为第i帧时域信号,h(n)为长度为N的短时窗系数,N是离散傅里叶变换的长度。
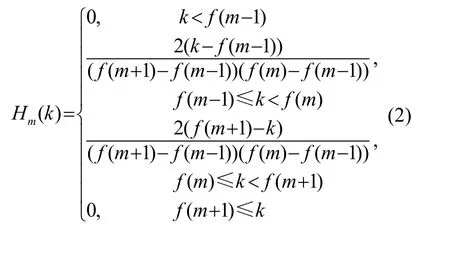
计算每个滤波器输出的对数能量:
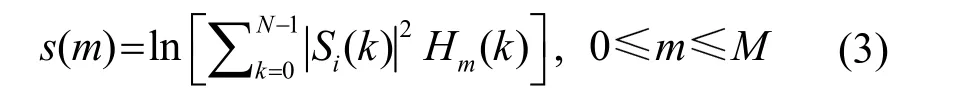
最后构成的特征图横轴为时间轴,纵轴为各个滤波器下输出的对数能量,维度等于滤波器个数。
3.2 NMF特征
NMF是一种无监督的矩阵分解方法,它使分解后的所有分量均为非负值,并且同时实现非线性的维数约减。给定一个非负矩阵V,它的目标就是分解得到一个非负的字典矩阵W和一个系数矩阵H,即求解如下优化问题:
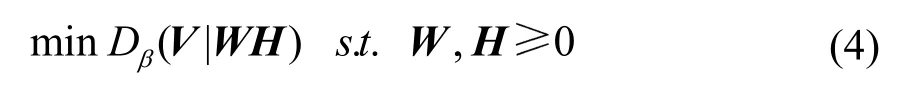
其中,Dβ表示分离方式。本文中,我们把β设为2,则Dβ为欧氏距离。利用NMF得到的系数矩阵,作为NMF特征使用。
3.3 融合特征
LME特征每一维都对应相应Mel滤波器输出的对数能量,在较好地表征音频信号的同时,降低了对应声谱图的维数,去除了大量冗余信息,减轻了计算复杂度。但是,使用Mel滤波器对声谱图进行平滑处理使得谐波结构(如图 3 中的机场音频样本声谱图的低频部分)这样的细节不再显著。图 4为该样本经过40维Mel滤波器组后的输出图像。从图4可以看出,原本低频部分存在的明显的谐波结构已经完全无法观察到。实际上,Mel滤波器组对其相应频带内频谱幅度进行了加权求和,从而实现降维处理,这就导致不同的频谱可能对应相同的滤波器输出,造成不同类别音频信号的 LME特征在某些子区域上很可能相似或相同。
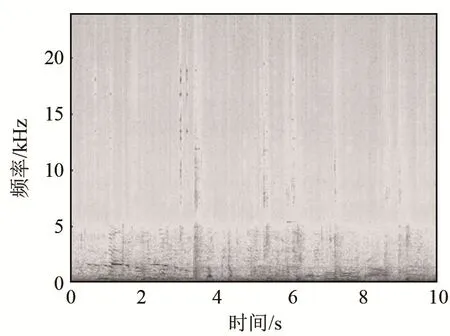
图3 机场音频样本声谱图Fig.3 Spectrogram of airport audio sample
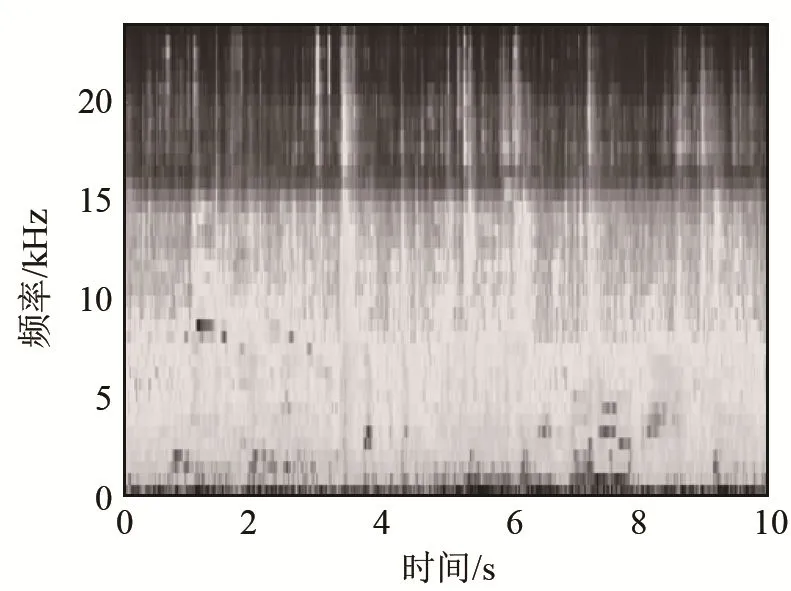
图4 LME特征图Fig.4 LME feature map
有效弥补 LME特征中丢失的细节,可以将声谱图上的典型谐波结构作为细节信息补充上去,以增加原始LME特征的区分度。为此,提出一种为细节特征与整体效果特征相融合的办法,对声谱图进行非负矩阵分解,之后将系数矩阵作为细节特征和LME特征相融合,在较少增加数据量和冗余信息的同时使得提取的特征具有更强的鲁棒性。
NMF特征采用乘性更新规则来优化提取。特征提取过程如下:
(1) 把声谱图矩阵作为待分解矩阵(1 025×500),将所有训练集样本的声谱图扩展成1 025×500N的二维矩阵,其中N为训练集的样本数。采用NMF,提取时间轴上的基,分解得到大小为1 025×40的字典矩阵W,如图5所示。图5横轴上的每一维(时间轴上的每一维)对应为字典的一个基。

图5 字典矩阵WFig.5 Dictionary matrix W
(2) 固定由步骤(1)得到的字典矩阵W,对每个样本的声谱图矩阵作NMF,得到40×500的非负矩阵系数H,如图6所示。这个矩阵H作为样本特征的一部分使用。
NMF分解得到的系数矩阵H保持了声谱的低频细节结构。图7为原始声谱图和NMF重构的声谱图。对比图 7(a)、7(b)可以看出,重构声谱图在高频部分存在一定的失真,而低频部分的谱细节还原较好。从矩形框中的部分可以看出,声谱图低频段的谐波结构基本没有失真。因此,利用系数矩阵H,可以构造表征细节的低维特征。
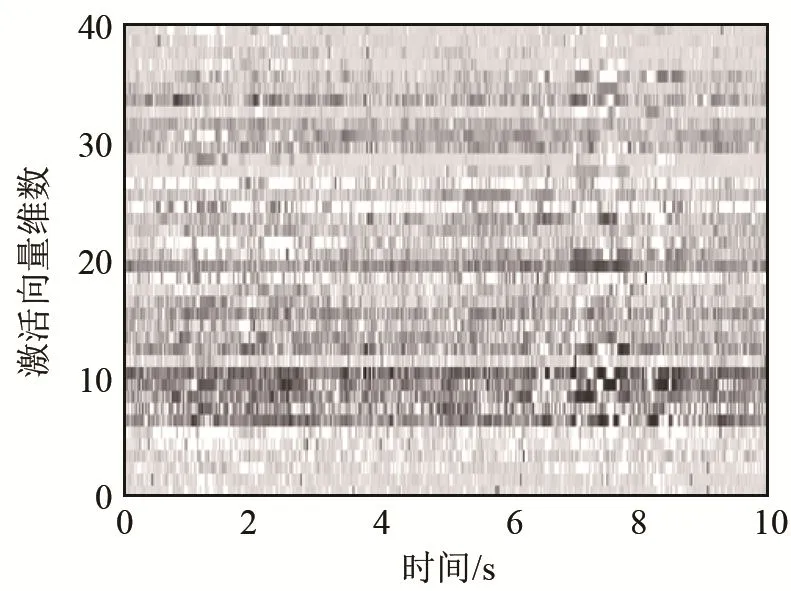
图6 系数矩阵HFig.6 Coefficient matrix H
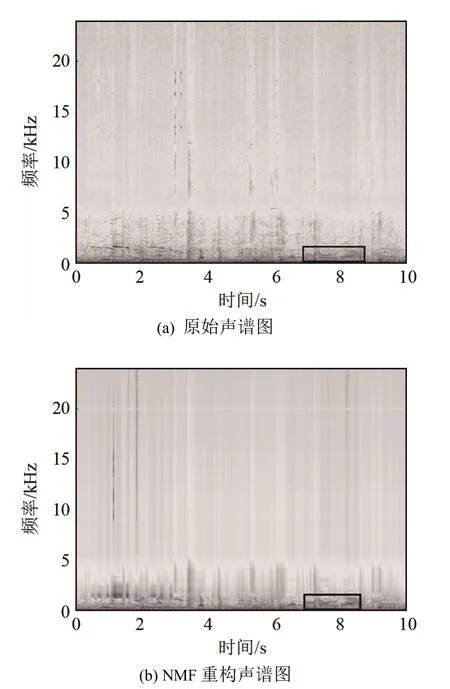
图7 原始声谱图和NMF重构声谱图Fig.7 Original spectrogram and NMF reconstructed spectrogram
4 实验结果与分析
采用对比实验的方法,分别验证所提出的LME+NMF融合特征和MCNN模型对ASC任务的有效性,并对实验结果进行分析比较。
4.1 实验数据
表2给出了DCASE2017和DCASE2018数据集包含的声学场景类别及场景数。
在DCASE2017的ASC任务中,开发集提供了包括15个真实声学场景的4 680个音频样本。每个场景的样本都记录于不同的地点,每个地点记录18~25 个样本,所有样本都是采样率为44.1 kHz、持续时间为10 s的双声道音频[15],分配在4个折叠当中。折叠为样本的构成方式,用来做交叉验证。以4折交叉验证为例,每次取1/4作测试,剩余3/4做训练。用4次结果的均值来衡量模型的性能好坏。
在DCASE2018的ASC任务中,开发集提供了包括10个真实声学场景的8 640个音频样本。这些样本记录于6个欧洲城市的不同地点,每个地点记录30~36个样本,所有样本都是采样率为48 kHz、持续时间为10 s的双声道音频[4],全部分配在一个折叠当中。

表2 实验使用的声学场景数据集Table 2 Acoustic Scene Datasets in the Experiments
4.2 基线系统
DCASE2017的基线系统是一个多层感知机模型,包含两层隐藏单元为 50的全连接层,隐层和输出层激活函数分别为Relu和Softmax,损失函数为交叉熵,学习率为0.001,优化器为Adam[16]。输入样本为单声道40维、500帧(10 s)的LME特征图,每帧长40 ms且有50%重叠。
DCASE2018的基线系统是一个包含两层卷积和两层全连接的CNN模型,卷积核大小为7×7,步长为 1,padding方式为 same,池化方式为最大池化,同时采用批量标准化和dropout,其余参数设置和DCASE2017基线系统相同。
4.3 结果分析
4.3.1 MCNN模型效果
为验证MCNN模型的效果,用MCNN模型分别与2017年和2018年的基线系统进行对比。实验中除模型外其余设置全部和基线系统相同,结果如图8和图9所示。
从图 8和图 9可以看出,MCNN模型在DCASE2017和DCASE2018数据集上都有较好的表现,在大多数声学场景类别上分类精度都有明显提高,在少数几个声学场景类别上和基线系统表现类似,平均分类精度都得到了明显提升,分别提升了5.9%和8.6%。
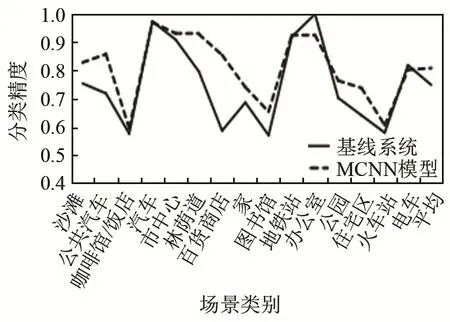
图8 MCNN模型与基线系统在DCASE2017数据集上的分类精度对比Fig.8 Comparison of classification accuracy between MCNN model and baseline system on DCASE2017 dataset
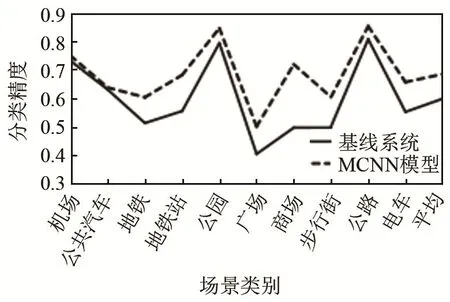
图9 MCNN模型与基线系统在DCASE2018数据集上的分类精度对比Fig.9 Comparison of classification accuracy between MCNN model and baseline system on DCASE2018 dataset
图10为基线系统和MCNN模型在DCASE2018数据集上的损失(Loss)曲线,可以看到,MCNN模型的损失曲线整体都位于基线系统损失曲线下方,说明模型在收敛效果方面要优于基线系统。
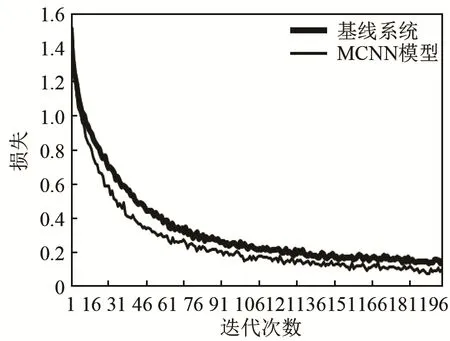
图10 MCNN模型与基线系统在DCASE2018数据集的损失曲线Fig.10 Loss curves of MCNN model and baseline system on DCASE2018 dataset
4.3.2 融合特征效果
为验证融合NMF特征和LME特征对分类效果的影响,在MCNN模型下分别使用40×500的LME特征和 40×500×2的融合特征进行对比实验,同样采用DCASE2017和DCASE2018数据集。
对比实验结果如表3和表4所示。可以看出,在DCASE2017数据集上,融合特征在15个类别中的 8个类别上相对 LME特征精度有所提高;在DCASE2018数据集上,融合特征在10个类别中的7个类别上相对LME特征精度有所提高,且平均分类精度分别提高了1.6%和1.7%。相比于基线系统,本文提出方案的平均分类精度分别提高了 7.5%和10.3%,用DCASE2017测试集数据进行测试,基线系统精度为61%,本文提出方案的精度为68.1%,提高了7.1%。
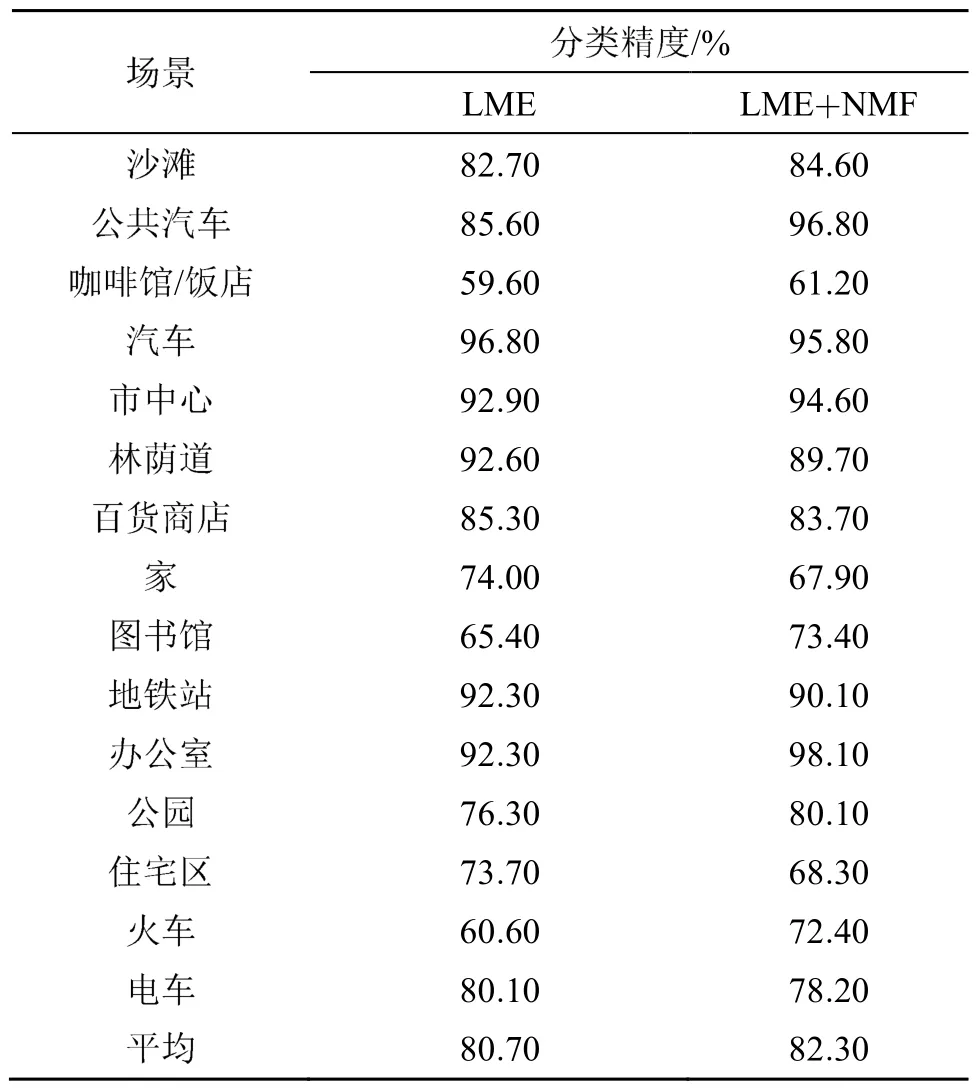
表3 DCASE2017数据集上的分类结果Table 3 Classification results on DCASE2017 dataset
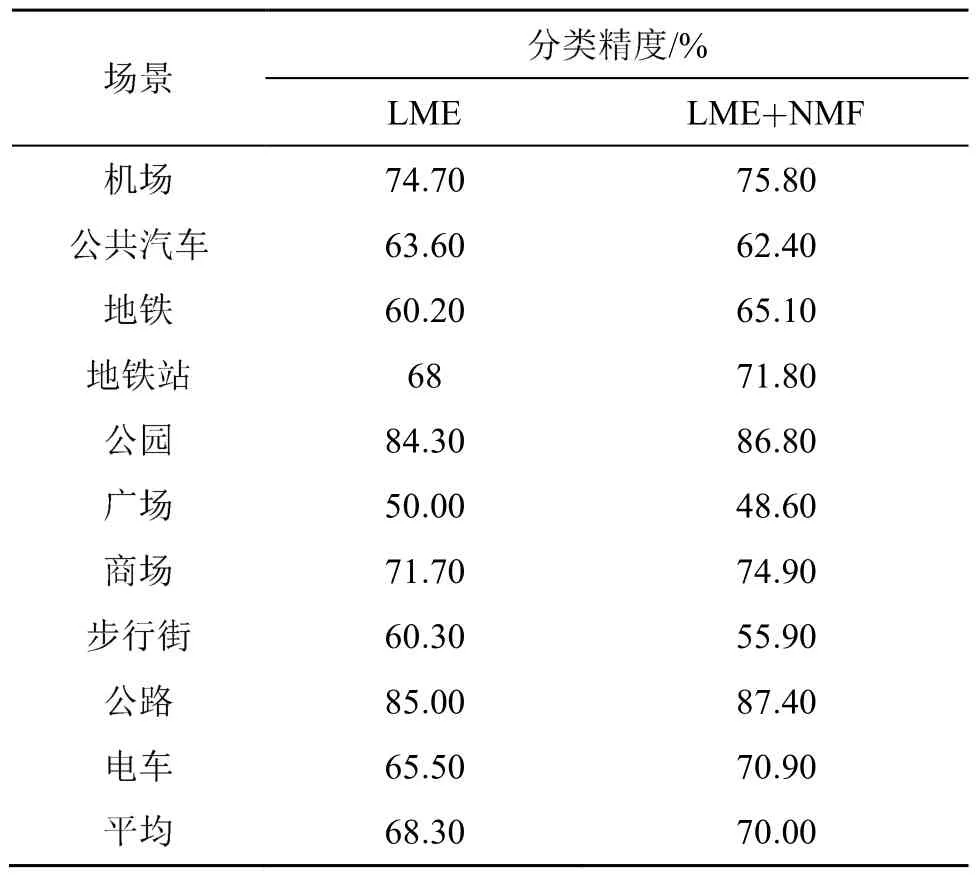
表4 DCASE2018数据集上的分类结果Table 4 Classification results on DCASE2018 dataset
5 结 论
本文针对声学场景分类任务,提出一种低维度的特征融合机制,融合了低层次的 LME特征和高层次的NMF特征,得到一种既包含整体包络信息又包括细节谐波结构信息的特征;提出适应于声音时频结构的多分辨率特征融合的 MCNN模型,使得模型可以从特征图中学习到更全面的信息。在DCASE2017和DCASE2018数据集上的实验结果表明,分类精度得到了显著提升,验证了本文所提方法的有效性。
