基于独立循环神经网络的跌倒检测方法

王晶晶， 黄 勇， 陈宝欣， 赵运勇

（1．烟台黄金职业学院机电工程系，山东招远265401；2．海军航空大学，山东烟台264001；3．重庆市软汇科技有限公司，重庆400039）

0 引 言

随着微型传感器和数字技术的快速发展，尤其是近年来人工智能在各领域的不断突破，各种智能的可穿戴设备不断涌现，广泛应用于跌倒检测领域，基于可穿戴设备的跌倒检测方法也获得了众多学者的关注。跌倒作为一种相对于正常姿态的异常行为，文献［1-2］中将跌倒定义为“非本意地摔倒在地面或者更低的平面上”。可以看出，跌倒有其固有的特色，但又与躺下、弯腰等行为有相似的地方，都存在一个设备的空间位置由高到低的变化。因此，可穿戴设备的跌倒检测面临着一定的困难和挑战。目前，常用的跌倒检测算法有直接阈值法和机器学习法等。直接阈值法通过人工提取特征值，然后与设定的阈值进行比较以确定是否属于跌倒状态。常用的特征值有加速度或速度最大值、方向变化、信息熵等。文献［3］中认为跌倒撞击的加速度大于2．5 g。文献［4］中将跌倒判决设为加速度高于1．8 g和同时角速度＞200°／s的行为。文献［5］中认为跌倒发生时，加速度会先高于某个阈值，随后又会低于某个较小的阈值，通过识别这一时间约束的状态变化来检测跌倒。通过上述研究结果可以发现，直接阈值法基于人工提取的特征值进行判断，计算简单，运算速度快，非常适合在嵌入式可穿戴设备上维持较长时间的运行。但是，直接阈值法的特征选取难以全面反映跌倒和非跌倒的数据特点，且阈值的选择没有理论依据，即阈值对误报率和漏报率的关系没有理论支持。机器学习的方法将跌倒检测的过程看作是一个二分类问题，常用的算法如人工神经网络、决策树、支持向量机和K近邻等。按照对数据处理方式的不同，机器学习的方法又可分为基于特征的方法和基于时间序列的方法。基于特征的方法类似于直接阈值法，不同的是其提取人工特征后，直接采用SVM等典型的分类器进行判决［5-7］。这种方法与直接阈值法都面临着特征提取不充分的问题。基于时间序列的机器学习方法认为传感器各个状态之间存在时间上的相关性，如跌倒过程会有一个失重、撞击的过程［5］。常用的方法有条件随机域、隐马尔科夫模型、循环神经网络等。理论上讲，这类方法由于采用端到端的黑盒训练法，不受人工特征提取不全面的影响。文献［8］中比较了RNN与SVM和一类神经网络（1NN）等方法的性能，结果显示1NN效果最好。实际的可能原因是原始的RNN训练存在梯度消失的问题，即如果输入时间序列过长的话，RNN将很难训练。文献［9］中将原始RNN引入跌倒检测，取得了较好效果，但是文中并未描述采用的时间序列长度。为了克服RNN梯度消失的问题，长短期记忆网络（Long Short Term Memory，LSTM）和门循环单元（Gated Recurrent Unit）被提出，但是由于“门”的引入，大大增加了计算量，因此文献［10-11］中基于多层LSTM的方法对于基于嵌入式系统的可穿戴设备来说并不适用。

作者前期研究了基于离散特征的神经网络跌倒检测算法［12-13］，本文在此基础上进一步提出了基于独立循环神经网络（Independently RNN，IndRNN）的跌倒检测方法，构建了双向、多层和残差结构的跌倒检测模型，并分析了不同网络结构和参数对训练的影响。实验结果显示，本文所提基于IndRNN的跌倒检测方法，相对于基于原始RNN的方法，性能上有较大提升，与LSTM网络性能相当。相比于前期工作，新方法降低了误报率。

1 基于IndRNN的跌倒检测方法

1.1 独立循环神经网络

RNN广泛应用于序列学习问题，如行为识别、语音识别等，并且取得了很好的结果。相比于卷积神经网络等前向网络来说，RNN可以将隐含的状态通过前一时刻传递到下一时刻，该过程用公式表示如下，

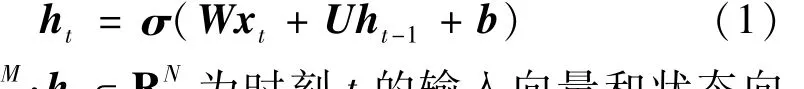
式中：xt∈R；ht∈R为时刻t的输入向量和状态向量；W∈RN×M，U∈RN×N和b∈RN分别表示输入权重、循环权重和偏执；σ（·）表示元素级激活函数；M和N分别为输入向量和状态向量的维度。LSTM和GRU通过引入门单元可以部分缓解该问题。文献［14］中提出了一种IndRNN结构，隐含层的每个神经元之间互相独立，可以实现非常深的时间步长。IndRNN的结构可表示为

式中：u为循环权重向量；◦为Hadamard积。对于第n个神经元，隐含状态hn，t可写为

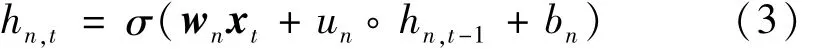
式中：wn和un分别为输入权重和循环权重。可以看出，每一个神经元只接收来自输入的信息和其自身的前一时刻状态。此外，为了获得更深的时间步长和网络层数，IndRNN引入了线性整流函数（Rectified Linear Unit，ReLU）激活函数，

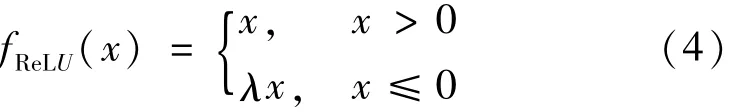
1.2 跌倒检测模型的构建

为了实现从传感器序列数据到检测结果的端到端处理，本文设计了基于IndRNN的跌倒检测模型，其结构如图1所示。

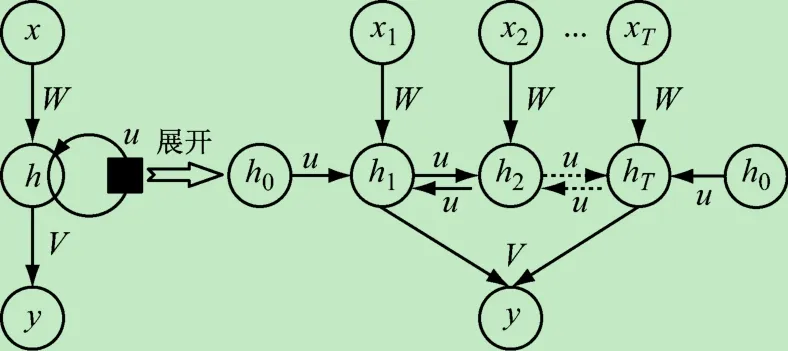
图1 跌倒检测模型结构图

模型结构主要有以下3部分组成：

（1）输入层。输入层的数据为传感器序列数据滑窗截取T个时间步长，即x1，x2，…，xT，其中每一时刻的数据为传感器当前状态矢量，可以是三轴加速度信息或三轴角速度信息等。

（2）隐含层。隐含层的主要参数为维度N，其激活函数采用ReLU。IndRNN的隐含层通过Hadamard积实现状态的转移。对于跌倒检测的时间序列而言，最终“跌倒”或“非跌倒”的状态信息隐含于整个跌倒过程。通过循环神经网络的记忆功能，这一过程的特征可存储于最终时刻T的状态向量和输出上。如果再将序列数据逆序输入另一个IndRNN单元，则最终跌倒特征会保存在初始时刻的输出。这前后两个时刻的输出是最为关心的。如果问题规模较复杂，单层的IndRNN网络结构可能不足以应对，此时可采取堆叠多层的办法增强网络的性能。需要注意的是，网络模型的复杂度与问题的复杂度是相关联的，过于复杂的网络结构反而容易造成过拟合。为此，本文将堆叠的每一层IndRNN的前后输出连通至输出层，这样可以降低网络带来的过拟合副作用。这种结构的基本原理是残差网络，通过残差跳跃式的结构可以使网络在纵向空间上达到很深的层次。当然，本文方法主要面向的是嵌入式系统应用，实际并不需要特别深的空间层次，2层的纵向深度已足够。

（3）输出层。经过双向IndRNN隐含层的处理后，关于跌倒或非跌倒的隐含特征得以提取，将两个方向的特征输入一个简单的分类器即可实现跌倒检测。本文采用0和1分别表示不跌倒和跌倒两种状态，因此输出层采用Sigmoid激活函数，即

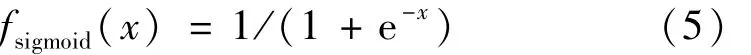
1.3 模型训练策略

训练神经网络常用的损失函数有交叉熵、均方根误差、SVM合页损失、Smooth L1损失等。对于跌倒检测这一问题，有两个指标需要重点关注：检测率和误报率。一般的跌倒检测设备在检测到老年人跌倒后会做出报警提示，如发出声响或者语音和短信呼叫亲属等。如果设备频繁发生误报，将严重影响用户体验，并且会造成对设备的信任危机。而如果检测效果不好，老年人在跌倒后不能有效警示，又会造成严重后果，进而也会降低对设备的信任。本文引入奈曼-皮尔逊准则，即在给定的虚警概率约束条件下，使检测概率达到最大。文献［15］中证明了采用交叉熵、均方根误差作为损失函数训练的神经网络或自适应系统是奈曼皮尔逊最优的，即在一定虚警条件下，相应检测概率是最大的（最终的近似效果受网络结构参数和训练情况影响）。为此，采用交叉熵作为损失函数，定义如下，

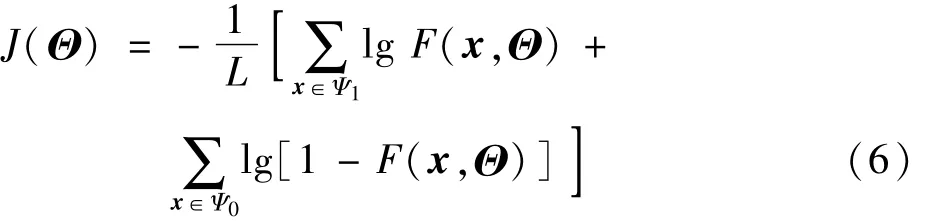
式中：L为总的样本数；Θ为网络的全部权重向量；F（x，Θ）为神经网络的输出。采用梯度下降算法作为网络优化算法，其基本原理如下：

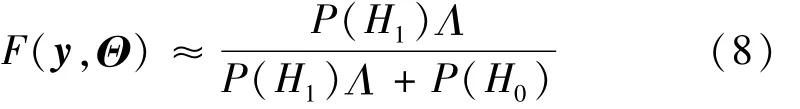
式中：Λ为似然比。通过设定一个阈值τ∈［0，1］与网络输出进行比较可控制跌倒检测器的误报率，并且可以保证当前的检测概率是最大的。这样做的另一个好处是对于最终面向用户的设备，可以设置一个设备灵敏度调节选项，用于用户自主控制设备的灵敏度。

2 数据采集与预处理

利用前期研制的可穿戴式跌倒检测设备采集各种跌倒与非跌倒的数据，采样频率设为50 Hz。该型设备采用三轴加速度传感器采集人体运动状态数据，并具有蓝牙无线传输模块、GPS定位、语音和短信通信能力［12-13］。通过将该设备佩戴于腰部位置，然后与上位机蓝牙建立连接，通过自研的软件系统可实时采集各种运动状态数据。各种类型的数据采集自9名志愿者（6名男性，3名女性），包括5种跌倒类型（走动跌倒、跑动跌倒、左侧跌倒、右侧跌倒以及无意识状态跌倒）数据，共415条，和常见的生活状态（走路、跑步、上下楼梯、躺下起立、坐下起立、弯腰、跳跃等）数据，共256条。为提高检测方法的计算效率和降低设备的计算负担，仅处理加速度值超过某一较小阈值的滑窗数据，因为如果加速度值仅超过9．8 m／s2很小时，完全可以认为当前处于非跌倒状态。取滑动窗口长度为3 s，对应T＝150个数据点。最终截取的跌倒数据样本401个，非跌倒数据样本642个。典型的跌倒与非跌倒（猛然坐下）滑窗数据如图2所示。由图中可见，跌倒与非跌倒数据有相似之处，即某一轴的加速度都在短时间内变化很大，因此，如果采用直接阈值法很可能造成误报。

3 实验及结果分析

实验采用TensorFlow深度学习框架搭建跌倒检测模型，采用第2节构建的数据集用于模型的训练和测试，其中60%的数据用于模型训练，40%的数据用于模型测试。本节采用交叉验证的方法测试了不同网络结构参数对模型训练的影响，包括不同类型的RNN、网络堆叠层数和隐含层的维度，给出了所提方法与相关研究的性能对比。训练设备为一台英伟达DGX Station，配备有4块英伟达Telsa V100显卡，因此可以很方便地并行训练各个模型，并验证训练效果。

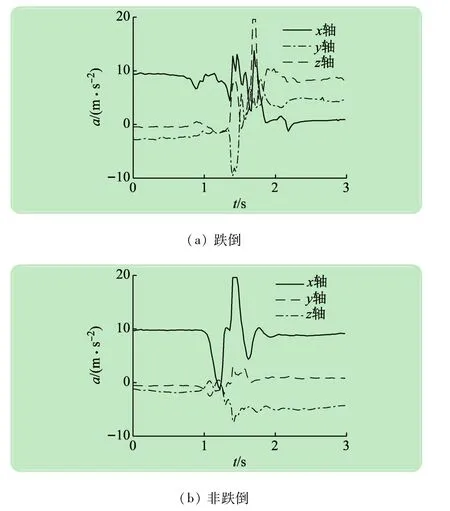
图2 典型的滑窗数据

首先比较原始RNN、GRU和IndRNN的效果，其中的GRU与LSTM类似，故仅以GRU为例。对于不同的网络结构，堆叠不同层数的RNN单元效果也不同。为此，分别比较了堆叠1层和2层的效果差异。所有模型的其余超参数设置相同，序列长度T＝150，输入向量维度M＝3，状态向量维度N＝8，学习率0．000 5，批大小406，迭代次数20 000，损失函数指标10－6。实验结果如图3所示，其中RNN／1／8表示1个RNN单元，状态层维度N＝8，其余类推。

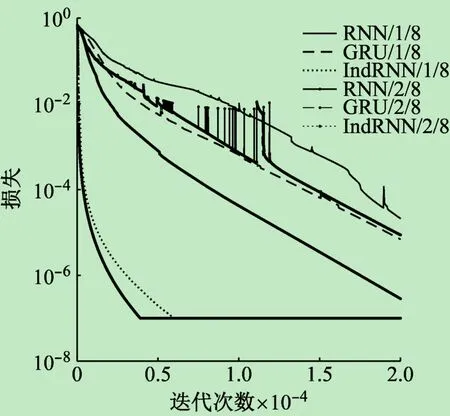
图3 不同网络结构训练损失

从图3可以看出，一方面，多层堆叠的方式可以提高模型的表示能力；另一方面，相较原始RNN，GRU结构中门单元的引入改善了梯度消失的影响，使模型的收敛速度加快。损失收敛最快的是基于IndRNN的模型，由此可见IndRNN独立状态单元和ReLU激活函数的引入大大降低了梯度消失的影响，使模型更容易记忆较长时间的信息。从图3还可以看出，RNN的训练过程存在损失波动，尤其是多层RNN堆叠时，原因可能是隐含层单元之间的互相影响，而具有独立隐含层结构的GRU和IndRNN梯度下降方向更稳定（GRU重置门和更新门功能类似于IndRNN中的状态权重u）。

状态向量的维度也直接影响模型的训练，不同维度的基于IndRNN的模型损失函数曲线如图4所示。从图中可以看出，IndRNN／2／8模型的收敛速度最快。

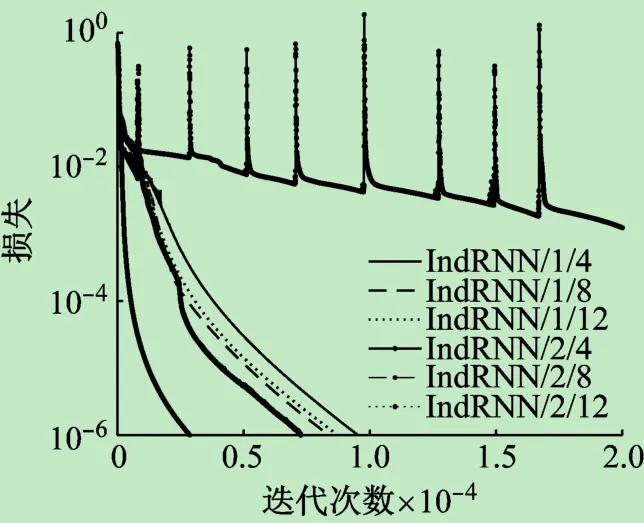
图4 不同隐含层维度训练损失

最后，取阈值τ＝0．997，测试本文方法与典型方法的检测率和误报率的性能，结果如表1所示。可以看出，本文基于IndRNN结构的方法明显优于阈值法，与早期的工作相比也有一定的提升，主要是大幅降低了误报率。与传统RNN的相比，检测率显著增加。本文的IndRNN／2／8结构与基于LSTM网络的方法检测率相当。实际上，现阶段各种方法的检测率已经相当高，本文方法的主要优势在于容易训练，且计算量较小。

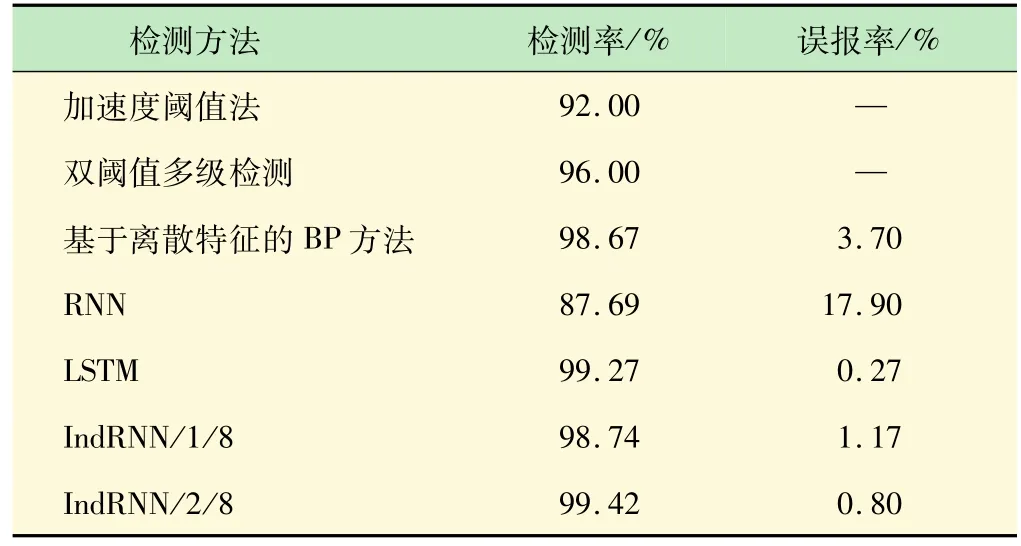
表1 不同方法检测结果比较

4 结 语

本文提出了一种基于IndRNN的跌倒检测算法，通过构建双向、多层和残差结构的跌倒检测模型，实现了从原始数据到跌倒判决的端到端处理。相比于基于特征值的阈值法，本文方法省去了人工提取特征值的过程。同时，采用交叉熵作为损失函数，通过最终阈值的设定，在控制误报率一定水平下，使得检测率最大，可以认为是一种基于奈曼-皮尔逊准则的检测器。实验测试了不同网络结构参数对模型性能的影响，结果显示基于IndRNN的跌倒检测方法更容易训练，检测率和误报率显著优于基于原始RNN的方法，与基于LSTM网络的方法性能相当。相比于前期工作，新方法降低了误报率。目前，本文工作主要是离线验证方法的有效性，后续工作将本文方法嵌入到实际系统中，以验证方法的实际性能。

·名人名言·

科学家不创造任何东西，而是揭示自然界中现成的隐藏着的真实，艺术家创造真实的类似物。

——冈察洛夫