相关于挠理论的（拟）连续模

李煜彦，何东林

（陇南师范高等专科学校 数信学院，甘肃 陇南 742500）

1 引言及预备知识

具有extending 性质的模类是内射模类的真推广，而（拟）连续模与extending 模和内射模都有着非常紧密的联系. 近年，许多作者研究了与（拟）连续模相关的问题. 1998 年，López-Permouth[1]提出了相对（拟）连续模的概念，讨论了（拟）连续模的性质及其等价刻画. 2007 年及2012 年，文献[2]和[3]分别提出了τ-CS模概念，其中τ=(T,F)表示遗传的挠理论. 2013 年及2017 年，文献[4]和[5]研究了相关于挠理论的奇异和非奇异模，这类模跟τ-CS模有非常紧密的联系. 2015 年及2017年，文献[6]和[7]分别研究了C3模和C4模，这些模与（拟）连续模有非常紧密的联系. 2011 年，Asgari等[8]给出了t-extending 模的概念，称模M 是t-extending 模，如果M 的每个包含Z2(M)的闭子模是M的直和因子. 2017 年，Asgari[9]在t-extending 模的基础上研究了t-连续模，证明了模M 是t-连续模当且仅当M 是t-extending 模和的自同态环是Von Neumann 正则环. 受此启发，本文提出了模M 是τ-N-（拟）连续模的概念，给出了模M 是τ-N-extending模的等价刻画，并对短正合序列0→ N1→ N → N2→ 0，证明了M 是τ-N-(拟)连续模当且仅当M 是τ-N1-和τ-N2-（拟）连续模.

本文中的环都是有单位元的结合环，模指酉右R-模. 称N 是M 的τ-稠密（纯）子模，如果是τ-挠(自由)模，记为 N ≤τ-dM(N ≤τ-pM)，用表示由M 的所有τ-稠密子模构成的集合. 称N是M 的τ-基本子模，如果 N ≤τ-dM 且N≤eM，记为 N ≤τ-eM，此时也称M 是N 的τ-基本扩张. 如果N 没有真τ-基本扩张，则称N 是M 的τ-闭子模. 称L 是N 在M 中的τ-基本闭包，如果 N ≤τ-eL，且L 是M 的τ-闭子模. 设 K,N ≤M,称K 是N 在模M 中的τ-补，如果K 是N∈ Dτ(M)}中的极大元. 设M ,N 是模，定义模族

由文献[1]知，A(N,M)关于子模、基本扩张和同构像封闭.

定义1[1]设M 是模，称M 分别是 N-extending模、N-连续模、N-拟连续模、如果M 分别满足N-(C1),N-(C1)和N-(C2),N-(C1)和N-(C3).

引理1[1]设M 是模，N≤M，K 是M 的直和因子，则K 是N 在M 中的补当且仅当 K∩N=0，且 K⊕N≤eM.

引理2[2]设M 是模，K ,N≤M，则K 是N 在M 中的τ-补当且仅当K 是N 在M 中的补，且K⊕N∈ Dτ(M).

由引理1 和引理2 易得如下引理.

引理 3设K ,N≤M，K 是模M 的直和因子，则K 是N 在M 中的τ-补当且仅当 K∩N=0，且K⊕N ≤τ-eM.

设M ,N 是模，定义模族

易知，Aτ(N,M)关于τ-子模、τ-基本扩张和τ-同构像封闭.

设 W=Aτ(N,M)，考虑如下3 个条件：

1）Nτ-(C1)对任意W∈ A，存在M 的直和因子K ，使得 W ≤τ-eK ;

2）Nτ-(C2)对任意W∈ A以及M 的任意直和因子L，如果，那么W 是M 的直和因子；

3）Nτ-(C3)对任意W∈ A以及M 的任意直和因子L，如果W 是M 的直和因子且 W∩L=0，W⊕L∈ Dτ(M)，那么W⊕L是M 的直和因子.

下面根据Nτ-(C1)，Nτ-(C2)和Nτ-(C3)条件，分别给出τ-N-extending模、τ-N-连续模、τ-N-拟连续模的概念.

定义2设M ,N 是模. 称M 分别是τ-N-extending模、τ-N-连续模、τ-N-拟连续模，如果M 分别满足Nτ-(C1)，Nτ-(C1)和Nτ-(C2)，Nτ-(C1)和Nτ-(C3).

显然，若M 分别是 N-extending模(N-连续模、N-拟连续模)，则M 分别是τ-N-extending模(τ-N-连续模、τ-N-拟连续模).

2 主要结论

先给出τ-N-extending模的等价刻画.

性质1设M ,N 是模，A=Aτ(N,M). 则以下等价：

1）M 是τ-N-extending模；

2）对任意L∈ A，存在M 的直和因子K ，使得 K∩L=0，且 K⊕L ≤τ-eM ；

3）对任意L∈ A，存在L 的τ-补K ，使得K 是模M 的直和因子；

4）对任意L∈ A，以及L 的任意一个τ-基本闭包N，存在M 的直和因子K ，使得K 是N 的τ-补；

5）对任意L∈ A，以及L 的任意一个τ-基本闭包N ，存在M 的直和因子K ，使得 K∩L=0，且K⊕L ≤τ-eM ；

6）对任意L∈ A，存在L 的τ-基本闭包N，使得N 是M 的直和因子；

7）对任意M 的τ-闭子模K ，若K∈ A，则K 是M 的直和因子.

证明1）⇒2）设 L ≤τ-dM ，由于M 是τ-N-extending模，故存在M 的直和因子K ，使得 L ≤τ-eK .设M=K⊕K′，由L≤K知，L∩K′=0. 又因为所以 L ≤τ-eK . 从而L⊕K′ ≤τ-eK⊕K′=M .

2）⇒3）由引理3 易证.

3）⇒4）设 L ≤τ-dM ，N 是L 的一个τ-基本扩张. 由3）知，存在L 的τ-补K ，使得K 是模M的直和因子. 于是有 N∩K=0，L⊕K ≤τ-dM 且L⊕K≤N⊕K≤M ，由引理3 知，N⊕K ≤τ-dM . 另一方面，设K≤B且 N∩B=0，N⊕B∈ Dτ(M)，因为K 是L 的τ-补，所以K=B，从而证得K 是N的τ-补.

5）⇒1）对任意 L ≤τ-dM ，设N 是L 的一个τ-基本闭包，则由5）知，存在M 的直和因子K ，使得 K∩N=0，且 K⊕N ≤τ-eM . 设M=K⊕K′，易知 L ≤τ-dK′，又由 L ≤τ-eK 可得，L⊕K ≤eN⊕K≤eM=K′⊕K. 从而 L ≤τ-eK′.

1）⇔6）及1）⇔7）由定义2 和文献[1][2]易证.

由 Aτ(N,M)的封闭性，易得下面结论.

性质2模M 是τ-M-（拟）连续模当且仅当对任意模N，M 是τ-N-（拟）连续模.

证明因为τ是遗传挠理论，所以 Aτ(N,M)关于τ-稠密子模、τ-基本扩张、τ-同构像封闭. 故Aτ(M,M)以及等于M 的τ-稠密子模构成的集合. 即结论成立.

定理1设M 是模，是短正合序列. 则以下结论成立：

2）M 是τ-N-extending模当且仅当M 分别是τ-N1和τ-N2-extending；

3）对任意 K∈Aτ(N,M)，存在使得 K=K1⊕K2.

证明1）不妨设 N1≤N，易得

另一方面，设 W∈Aτ(N2, M)，则存在 X ≤τ-dN2以及 f∈Hom(X,M)，使得 f(X)≤τ-eW . 而由g 满知，存在Y≤N，使得 X=g(Y). 从而 f(X)=f(g(Y))≤τ-eW ，即 W∈Aτ(N,M).

2）充分性. 设M 是τ-N1和τ-N2-extending模. 不失一般性，不妨设设W∈Aτ(N,M)，则存在 X ≤τ-dN 以及 f∈Hom(X,M)，使得 f(X)≤τ-eW . 令K 是W 在M 中的τ-闭包，K′是 f(X∩N1)在K 中的τ-闭包. 则下证K 是M 的直和因子即可.

由K′∈ Aτ(N1,M)以及M 是τ-N1-extending模知，K′是M 的直和因子. 则存在K′≤M，使得M=K′⊕K′故是标准投射. 令显然h是同态映射. 设 0≠y∈ K∩ K''，由于则 存 在 r∈R, x∈X ，使 得 0≠yr=f(x)=πf(x)=h(x+N1)，所以因 为，K∩ K′是K的τ- 闭子模，因而也是M的τ- 闭子模，又K∩K′∈Aτ(N2, M)以及M 是τ-N2-extending模知，K∩ K′是M的直和因子. 故存在L≤M，使得M=(K∩ K′)⊕L. 于是

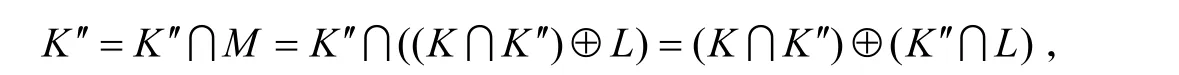
即K∩ K′也是K′的直和因子，从而 K=K′ ⊕(K∩ K′)是M 的直和因子.

必要性. 由1）易得.

3）由2）的证明过程知，对任意 K∈Aτ(N,M)，存在 K1,K2≤M，使得 M=K1⊕K2，K1≤K，且K=K∩ M=K∩(K1⊕K2)=K1⊕(K∩ K2)，其中 K1∈Aτ(N1, M),K2∩K∈Aτ(N2, M).

下面给出M 是τ-N-（拟）连续模的等价刻画.

定理2设M 是模，是短正合序列，则M 是τ-N-（拟）连续模当且仅当M 是τ-N1和τ-N2-（拟）连续模.

证明充分性. 设M 是τ-N1和τ-N2-（拟）连续模，则由定理1 知，M 是τ-N-extending模. 下面先证M 满足Nτ-(C3)条件.

设W 和L 是M 的直和因子，且 W∈Aτ(N,M), W∩L=0, W⊕L∈ Dτ(M). 由定理1 的3）知，存在 A1∈Aτ(N1, M)和 A2∈Aτ(N2, M)，使得 W=A1⊕A2. 因为M 是τ-N2-拟连续模，故 L⊕A2是M 的直和因子，从而 W⊕L=(A1⊕A2)⊕L=A1⊕(A2⊕L). 即W⊕L是M 的直和因子，所以M 是τ-N-拟连续模.

再 证M 满 足Nτ-(C2)条件. 设 W∈Aτ(N,M)，L 是M 的 直 和 因 子，且W≅L. 于 是 存 在A1∈Aτ(N1, M)和 A2∈Aτ(N2, M)，使得 W=A1⊕A2. 且 A1和 A2都同构于M 的直和因子，由M 是τ-N1和τ- N2-连续模知，A1和 A2都是M 的直和因子，从而W 是M 的直和因子. 所以M 是τ-N-连续模.

必要性. 由定理1 易证.

由定理2 容易得到，τ-N-extending（拟）连续模关于有限直和是封闭的.

推论1设M ,是模，若M 是τ-Ni-extending （拟）连续模(i=1,2,…,n)，则M 是τ-N-extending（拟）连续模.