一类由微分算子定义的具有复阶的亚纯函数类的Fekete-Szegö 问题

宋园

（滁州职业技术学院 基础部，安徽 滁州 239000）

1 引言及预备知识

S*(β)表 示∑中 满 足Re{- zf′(z)f(z)}＞β(z∈ U*,0≤β＜1)的 全 体 函 数 类，C*(β)表 示∑中 满 足Re{- 1- zf′(z)f′(z)}＞β(z∈ U*,0≤β＜1)的全体函数类，S*(β)和C*(β)称为β 级亚纯星象函数与β 级亚纯凸象函数.

对于任意的 b, c∈ℂ(c≠ 0,1,2,…)，Liu 和Srivastava[1]引入的亚纯函数上的Carlon-Shaffer 算子[2]定义如下：

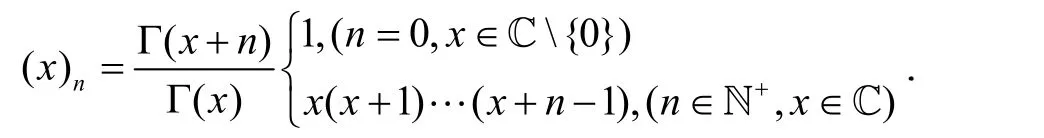
类似于Al-Oboudi[3-4]定义的算子，定义如下的微分算子：

如果 f(z)∈∑由式（1）给出，由式（2）、（3）、（4）得

当算子中的一些参数取特殊值时，就得到了我们熟知的算子，例如：

1）b=c=1时Al-Oboudi[5]研究了算子

2） n=1, μ=0时，Liu[1]研究了算子

3） b=c=μ=1时，Srivastava[6]研究了算子

令∑*(φ)表示满足下列条件的函数类：此函数类是由Silverman 等在文献[8]引入的. 很明显，当

2013 年，Aouf[9]研究了亚纯函数类的Fekete-Szegö 不等式.

定义 1设φ(z)是U 内具有正实部且满足 φ(0)=1, φ′(0)＞0的解析函数，它把区域U 映照到一个关于实轴对称且关于1 星型的像域上. 如果 f(z)∈∑，满足下列条件：

最近许多作者[10-11]研究了算子定义的解析函数类上的Fekete-Szegö 不等式，但很少有作者研究亚纯函数上的Fekete-Szegö 不等式，本文利用微分算子定义了一类亚纯函数并研究了其Fekete-Szegö 不等式，推广了已有的结果.

为得到结论，需要下面的引理：

引理1[12]设在U 内解析，且Rep(z)＞0，则

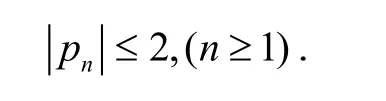
引理2[13]如果是U 内具有正实部的解析函数，则对任意的t∈ℂ，有等号在函数时成立.

引理3[14]如果 p(z)=1+ c1z+c2z2+c3z3+…是U 内具有正实部的解析函数，则对任意的t∈ℝ，有

同时，当0＜t＜1 时不等式可以改进为：

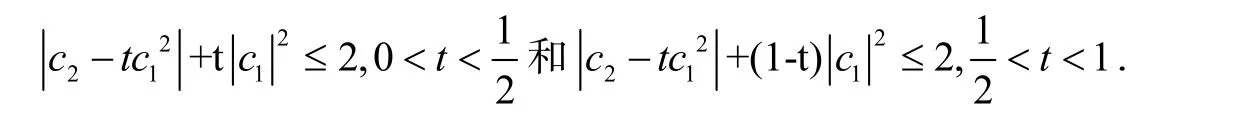
2 主要结果

定理1设则有

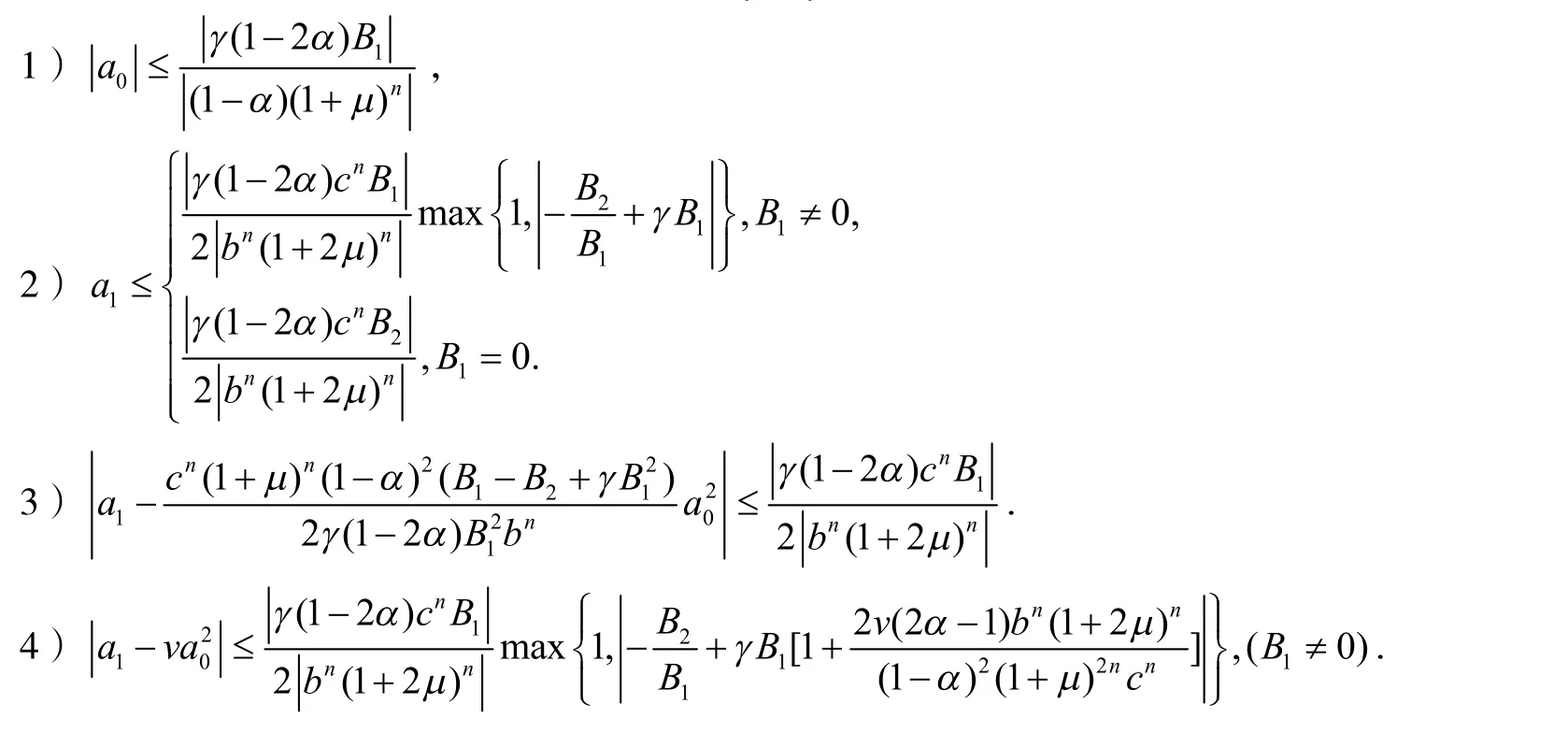
证明令

则

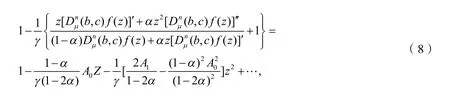
由式（5）得

令

则式（12）等价于

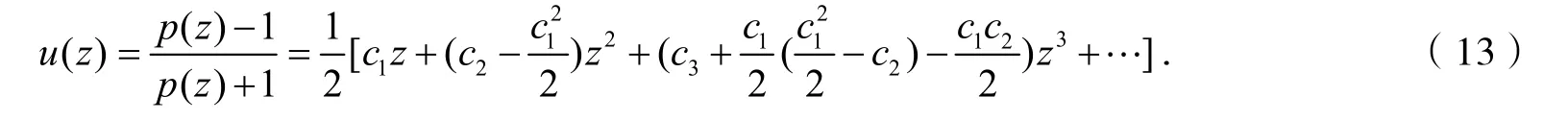
由式（11）、（13）得

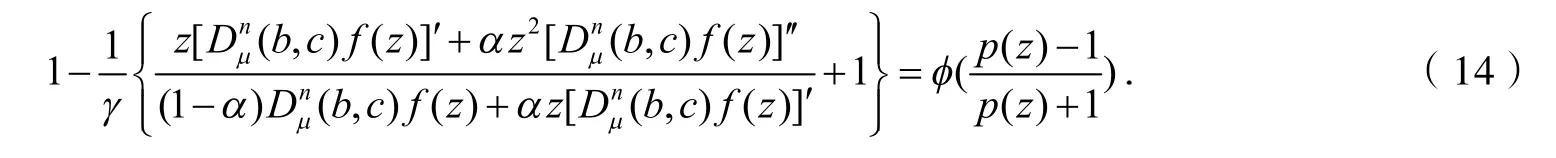
由式（13）、（6）得

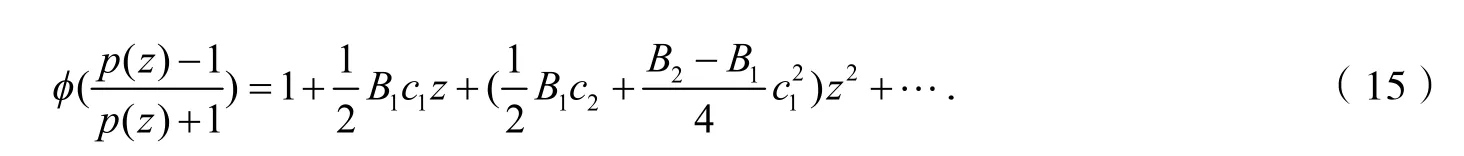
由式（8）、（9）、（10）、（15）比较z 和 z2的系数，得

由式（16）得

由式（18）及引理1 得

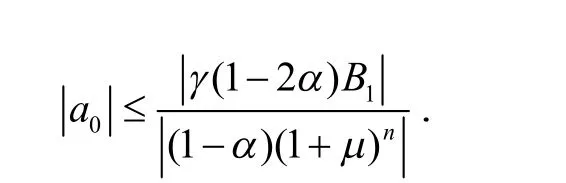
由式（17）和（18），得

由式（18）、（19）及引理1，得

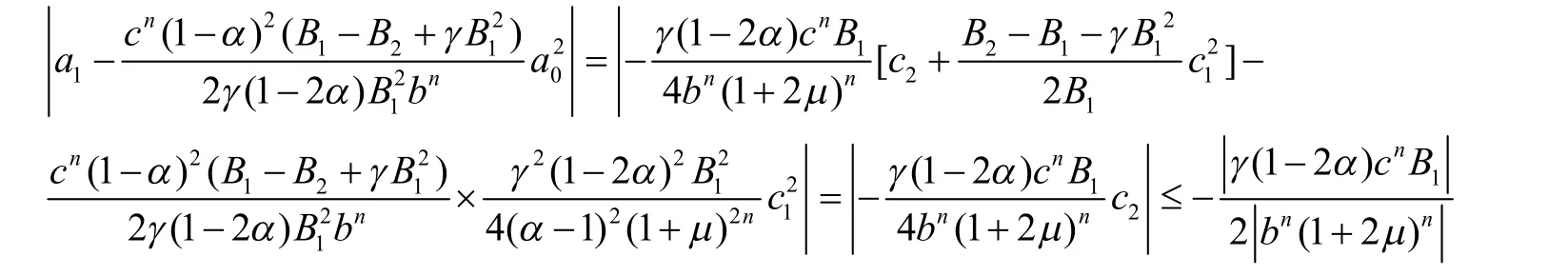
由式（18）、（19）及利用引理2，当 B1≠0 时，得

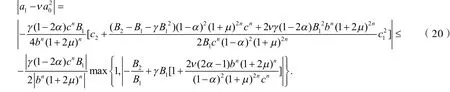
当 B1=0 时，由式（16）、（17）得则由引理1，得定理得证.

注释1令当γ=1时，定理1 的式（2）、（4）变为文献[9]中的定理1. 下面讨论μ∈ℝ 的情况.

定 理 2设如果 f(z)由式（1）给出，并且，则对任意的μ∈ℝ，有

证明由式（20）及引理3，可得定理2.

注释 2令 b=c, n=μ=0,(b,c)f(z)=f(z). 当γ=1时，定理 2 变为文献[9]中的定理 2. 若ν1＜ν＜ν2，根据引理3，定理2 可以被改进为：

定理3设由定理2 给出，且则

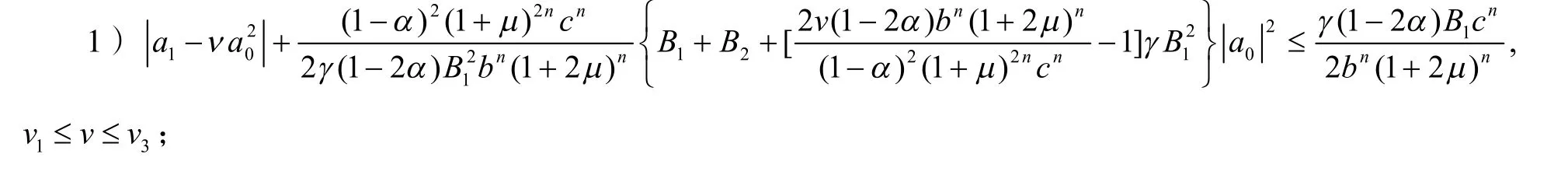
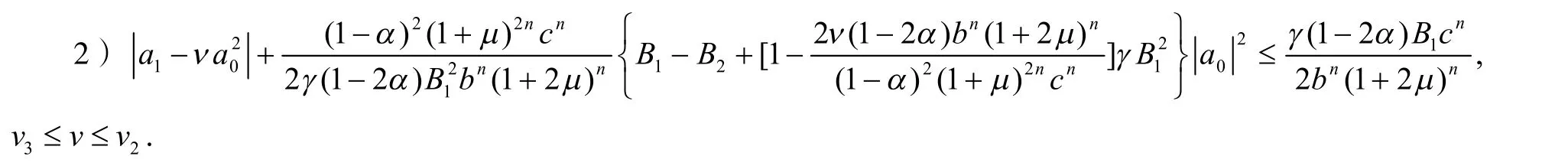
证明略.

注释3令当γ=1时，定理3 变为文献[9]中的定理3.