广义二元有向De Bruijn 图的限制弧连通度
2020-09-14黄艳平欧见平
黄艳平,欧见平
(五邑大学 数学与计算科学学院,广东 江门 529020)
1 引言及预备知识
令G 是Moor-Shannon 通信网络模型的拓扑结构图[1]. 图G 边(信道)以相同的概率p 独立发生故障,其中0<p<1 ,图G 的可靠性(即它保持连通的可能性)可以用以下的可靠多项式表达:
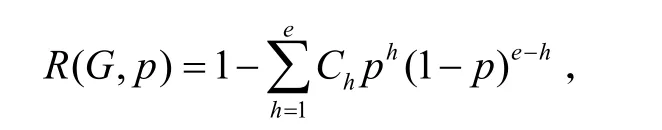
其中,Ch表示阶数为h 的边割的数量,e 表示图G 的边数. Prowan 指出要确定所有的系数Ch是一个NP 困难问题[2],传统的方法主要通过图的连通度来优化和近似估计网络的可靠性,后来人们提出了图的限制边连通度这一更加精确的工具[3-4].
定义1限制边割是将连通图G 分割成阶数至少为2 的连通分支的边割,连通图G 的最小限制边割所含的边数称为此图的限制边连通度.
本文中,用 λ2(G)表示一个图G 的限制边连通度. 有向图的相关定义如下:
定义2限制弧割是将有向连通图D 分割成阶数至少为2 的双向连通分支的弧割,图D 的最小限制弧割的边数称为它的限制弧连通度.
对有向图G 的任意子集X 或V(G)的任意子集X ,记G-X 为从G 中去掉X 中的顶点后得到的图,G-{w}简写为G-w . 记图G 的两个不相邻的子图或V(G)的两个不相邻的子集为X 和Y ,用(X ,Y) 表示从X 到Y 的弧集,记[X,Y]=(X,Y)∪(Y,X). 令是 有向图 G的顶点集},其中,X=V(G)- X . 对于阶数至少是4 且它的基础简单图不是星的连通有向图,有 λ2(G)≤ξ(G)[3].当网络的信道的发生故障的概率p 充分小时,在具有相同节点和信道的情况下,具有更大的限制边连通度和更少的最小限制边割的网络,则其局部可靠性更高[5-6]. 因此,优化限制边连通度和弧连通度对于设计具有更高可靠性的网络具有重大意义. 对于这个问题的研究已经有许多的进展,详情参见文献[6]. De Bruijn 图、广义De Bruijn 图和d 元连续图都是有名的网络拓扑图[7-10]. 广义的有向二元De Bruijn 图 BG(2, n)的顶点集为 V(G)={0,1,2,…, n-1},(x, y)是它的弧当且仅当 y≡2 x+α(mod n),其中,α∈{0,1}. 本文确定了 BG(2, n)的弧连通度,结果表明:当n≥7时 BG(2, n)是极大限制弧连通.
2 弧连通性
对于满足条件1≤d≤n- 1,1≤q≤n- 1和1≤r≤n- 1的非负整数 d,n, q, r,d 元连续有向图有n 个顶点,每个顶点分别用模n 的余数标记,存在从i 到j 的弧当且仅当 j≡qi+r+k(mod n),其中k∈{0,1,2,…, d-1}[7,8,11].
引理1[7]令d≥2,gcd(q, n)d,则 G(d,n, q, r)的链连通度至少为d- 1. 而且当q ≠±1 时,d- 1条使 G(d,n, q, r)不连通的弧必来自同一个顶点或去到同一个顶点.
引理2在 G(d,n, 2,0)中,只有顶点0 和n- 1有环.
证明令x 是 G(d,n, 2,0)的一个顶点. 如果x 有环,则 x≡2x+k(mod n),其中 k∈{0,1}. 因此,x +k ≡0(mod n). 如果k=0,有唯一解x=0;如果k=1,有唯一解x=n- 1. 证毕.
引理3令是 BG(2, n)的弧割且如果n≥4,则S≥2.
证明注意到 BG(2, n)=G(2, n, 2,0). 因为每一个顶点的出度与入度都是2,所以令G′是一个二部图,其具有顶点集{0,1,2, …, n-1}∪{0′, 1′, 2′, …,(n-1)′},其中i′j 是G′的边当且仅当(i, j)是 BG(2, n)从i 到j 的弧.
首先,我们证明:G′是圈. 只需证明:对任意两个连续的顶点v 和 v+ 1(mod n),G '有顶点u′,使得(u′, v)和(u′, v+1)都是它的边,或者说,BG(2, n)有顶点u,使得(u,v)和(u,v+1)是它的弧. 因为gcd(2, n)=1,所以,v ≡2x(mod n)有唯一的解x=u. 我们将G′作在图 1 中. 值得注意的是,属于{0,1,2,…, n-1}的顶点在圈 G '中连续排列,而且,在这个序列中依次插入点其中,k′插在2k 和2 k+1 之间,插在2 k+1 和2(k +1)之间,这里,此结构性质是以下推理的基础.

图1 BG 对应的图G′
如果A 是连通的,由G′ 的结构性质可知,X 中的点是连续的,记 X={i,i+1, i+2,…, j}. 令则2 x≡1(mod n). 因为n≥4,所以3≤x≤n- 2. 由条件得到因此,{i+x, i+1+x, j- x, j- 1- x}∩ X=Ø. 因为2(i+x)≡ 2i +1(mod n),如果2i+1∉ X,则(i,2i +1(mod n))是从X 到的弧;否则,(i +x,2(i +x))=(i+x, 2i+1)(mod n)是从到X 的弧. 因此,点对{i, i+x}是导出一条X 与之间的一条弧. 类似的,{ i +1, i+1+x}也导出X 与之间的一条弧.
对于点对{j ,j- x},如果2 j∉X,则(j ,2j(mod n))是从X 到的弧;如果2 j∈ X,则2(j- x)+ 1≡2j∈ X ,因此{j-x, 2 j}导出X 与之间的一条弧. 无论哪种情况,{j ,j- x}都导出X 与之间的弧. 类似的,{ j-1,j- 1- x}对应X 与之间的弧. 因为这些点对分别对应X 和之间的4 条不同的弧,所以,X 与之间至少有4 条弧. 因此,当A 连通时引理成立. 如果A 不连通,则G′至少包含4 个连通分支. 因此,引理也成立. 证毕.
引理4令是 BG(2, n)的弧割,且如果n≥4,则
证明根据引理3,我们只需要考虑gcd(2, n)=2 的情形. 对n 进行归纳证明. 当4≤n≤6 ,引理是成立的,所以假设n≥8. 在这种情况下,将 BG(2, n)的点集划分个子集其中在每一子集中,所有的顶点都有相同的外邻点. 令H 是如下定义的有向图,它的顶点是是H 的弧 当且 仅 当(i, x)∈E( BG(2 ,n)),其 中,易见,H 与同构. 图H 的每一条弧都对应 BG(2, n)的两条弧,且只有有环.
情形1.在这种情形下,每一个顶点都贡献了两条X 与之间的弧(因为中的点都有两个相同的外领点). 如果H 至少有两个这样的顶点则如果H 中只含有一个这样的顶点,则(因为). 因此,这表明
情形2.XH=Ø 或不失一般性假设 XH=Ø. 注意到,如果中有一个顶点属于X ,则所以,这个点贡献了两条X 与之间的弧. 因为这些点至少贡献了6 条弧给因此证毕.
定理1当n≥4时,BG(2, n)是极大弧连通的,即 λ2=2.
证明令是 BG(2, n)的一个最小限制弧割,其中如 果则如果顶点0 与n- 1相邻,则有 n- 1≡2 × 0+k(mod n),其中k∈{0,1}. 但是,由于n≥4,这种情况是不可能的. 类似地,(n-1,0)也不是一条弧. 由弧(0,1)的出度为2 可得:ξ(BG(2, n))=2. 因此,在这种情况下有如果根据引理3 得,因此,证毕.
