单位根原假设下的持久性变点检验
2020-09-14秦瑞兵王文华
秦瑞兵,王文华
(山西大学 数学科学学院,山西 太原 030006)
0 引言
在过去二十多年中,越来越多的证据表明,经济和金融时间序列呈现出持久性变化,特别是通货膨胀率序列、短期利率、财政赤字和实际产出。由于序列的平稳性决定着数据建模方法的不同,持久性变点问题在实际应用中有较大的价值,因此吸引了较多研究者的兴趣。Kim等[1-2]提出了比率统计量来检验持久性变点问题。Busetti和Taylor[3]应用比率检验进一步研究了原假设是序列具有确定性趋势函数时持久性变点检验问题。Han等[4],Chen等[5]则运用比率方法讨论了方差无穷厚尾序列持久性变点的检验和估计问题。Chen和Tian[6]基于核回归残差提出比率统计量对非参数回归模型在固定和随机设计情形下的方差变化进行了监测。Yang和Jin[7]则讨论了新息为厚尾情形的持久性变点检验问题。Chen[8]通过滑动核加权方差比率统计量来监测方差无穷序列的持久性变点。Kejriwal[9]基于序贯检验给出了一种持久性变点个数的估计。
上述这些研究都是在原假设为平稳过程下,采用比率方法对持久性变点问题做了分析,而诸多宏观经济数据大多为单位根过程。当过程为单位根过程时,以上结果会出现经验水平扭曲的问题,因此Banerjee等[10]和Leybourne等[11]均采用DF型比率统计量对原假设为单位根过程的持久性变点问题进行了分析。Leybourne等[12]进一步分析了上述DF型比率统计量在含有持久性变点的备择假设下的渐近性质。但文献[12]的模拟表明,该DF型检验统计量不能较好地控制经验水平,为此本文采用回归残差比率的方法来检验在原假设为单位根过程的持久性变点问题。数值模拟结果表明,与文献[12]相比,本文检验能很好地控制犯第一类错误的概率,较大地改善了经验水平的扭曲现象,在有限样本下有较好的经验势,并且当原假设为平稳过程,本文方法的经验水平也较文献[12]有所改进。
1 主要结果
考虑时间序列模型
(1)
其中ρ1,ρ2≤1是未知参数,k*=[Tτ*]是未知变点,[Tτ*]表示不超过Tτ*的最大整数,随机项ut满足以下的假设条件:
假设1
(1)E(u)=0;
(2)E|u|γ+ε<∞,γ>2;
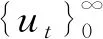
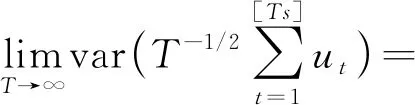
基于(1)式的数据生成过程,原假设H0:随机过程{yt}在整个样本区间上是一个单位根过程,即ρ1=ρ2=1;备择假设为H01:随机过程{yt}在时刻[Tτ*]从平稳过程变化到单位根过程,即ρ1<1,ρ2=1,或者备择假设为H10:随机过程{yt}在时刻[Tτ*]从单位根过程变化到平稳过程,即ρ1=1,ρ2<1。
针对上述假设检验问题,定义
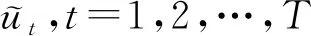
定义下面的比率检验统计量
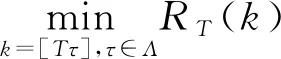
定理1 在假设1成立的条件下,在原假设H0下,有
其中“⟹”表示弱收敛,
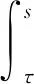

其中
当原假设成立时,由假设1可知,对于
及
其中W(r)是维纳过程,并且由Chan和Wei[13]的泛函中心极限定理和连续映照定理得
T-3/2S1,[Ts](k)=
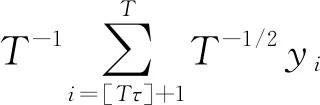
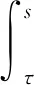
从而
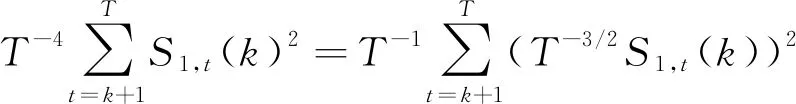
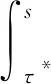
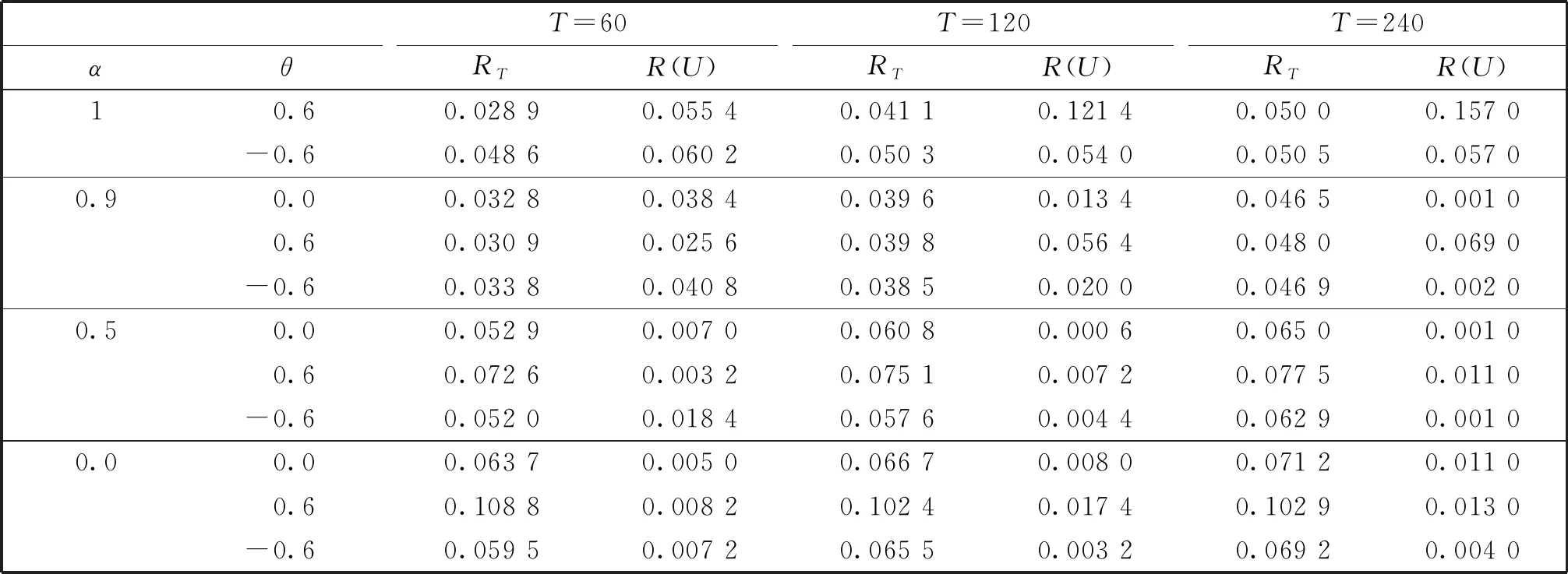
同理对于0 T-3/2S0,[Ts](k)= 因此 故由连续映照定理得 证毕。 定理2 在假设1成立的条件下,在备择假设H01下,有 其中“⟹”表示弱收敛, 证明当备择假设成立时,可能的变点位置存在两种情形:第一种情形是位于真实变点位置k*之前,即0 1) 对于第一种情形0 对于统计量的分子部分,当τ≤s<1时, (2) 并且由连续映照定理得,τ*≤r<1, -W(τ*)}dr≡σuψ3(τ,s), (3) 则 从而可得 2) 对于第二种情形k*=[Tτ*] 根据(2)式和(3)式的证明易得出,τ*≤r≤τ, 0 从而 最后综合第一种情形和第二种情形的结果,可以得到 证毕。 注:定理2表明该统计量将以速度T2发散到无穷大,且其势函数与真实变点位置有关。 本节通过数值模拟分析本文检验方法的有限样本性质,并将新方法的经验水平和势与文献[11]提出的R统计量进行了比较。为模拟本文统计量RT的临界值,先生成T个独立同分布的正态随机数,由泛函中心极限定理可以获得维纳过程的一次实现,再应用随机积分的定义得到极限分布的一个观测值,重复观测10 000次得到经验分位数。表1列出了不同样本量下经10 000次循环得到的临界值。 采用如下模型 yt=αyt-1+εt-θεt-1,t=1,2,…,T, 并设参数α=(1, 0.9, 0.5, 0.0),θ=(0, 0.6, -0.6)生成模拟数据。分别取样本量为60,120和240,在5%检验水平下模拟经验水平。表2给出了RT统计量在不同参数组合下经5 000次循环得到的经验水平,并与文献[12]的方法进行了比较。从结果可以看出:(1)在单位根原假设下,文献[12]的R统计量经验水平扭曲较大,尤其是当θ=0.6时,经验水平随着样本量的增加有逐渐增大的趋势,这使得在区分序列是服从单位根还是存在变点时更容易拒绝单位根原假设。和文献[12]相比,本文统计量的经验水平随着样本量的逐渐增大而逐渐接近于设定的检验水平,尤其当样本容量为T=240时能很好地控制经验水平,说明本文的统计量能较为准确地区分序列中是否存在持久性变点的情况。(2)对于平稳性原假设,文中统计量的经验水平仍然更为接近预先设定的检验水平,因此,即便检测序列是平稳的,但只要没有持久性变点,本文的检验也不会拒绝无变点的原假设。 表1 临界值 表2 经验水平 采用数据生成过程 设参数α=(0.9, 0.5, 0.0),τ*=(0.3, 0.5, 0.7)。分别取样本容量为T=60,120,240,在5%检验水平下做模拟,得到经验势。表3给出了文中统计量在不同参数组合下经5 000次循环得到的经验势函数。由表可见:(1)变点位置越靠后时经验势最高,说明变点位置较靠后时更容易检测出变点的存在。(2)随着样本量的增加,经验势函数在增加。(3)与Leybourne等[11]的R统计量相比,本文统计量总体上有更高的经验势。 基于回归残差,本文应用比率统计量研究原假设为单位根过程的持久性变点检验问题,在原假设下得到渐近分布,同时得到备择假设下的一致性。数值模拟结果表明,本文方法能很好地控制经验水平,在备择假设下较靠后的变点都有很好的检验效果,甚至在平稳原假设下经验水平也能较好地接近设定的检验水平,因此不会拒绝无变点原假设。此外,本文假设为AR(1)模型,应用BN分解定理,可将本文结论推广到一般线性过程。
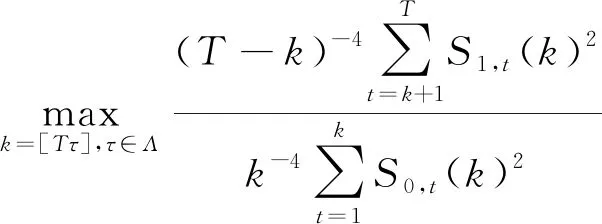

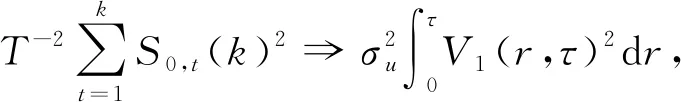
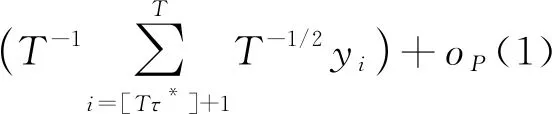

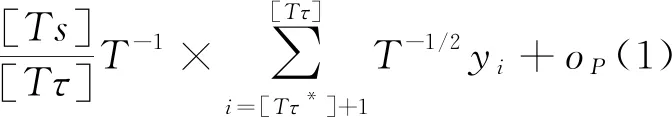



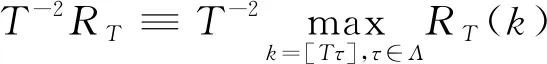
2 数值模拟

3 结论
