基于激光散斑的实时立体匹配算法及其应用

潘创 刘乙奇 黄道平

(华南理工大学 自动化科学与工程学院，广东 广州 510640)

双目立体视觉旨在模仿人的双眼，根据目标在左右两幅图像中的位置偏差(即视差值)恢复目标的三维信息。随着社会的不断进步和需求的不断提高，双目立体视觉也随之成为了当前研究的热点和难点问题，数十年来大批学者对这一领域进行了深入的研究，取得了大量的成果。立体匹配是双目视觉的关键步骤，匹配的精度和速度制约着双目视觉系统的应用和发展。对于给定的两幅图像，因为相机的安装位置不同，同一个目标在两幅图像中的位置并不相同，立体匹配就是确定同一个目标在两幅图像中的位置的过程。目前，立体匹配算法可分为局部匹配算法和全局匹配算法[1]。局部匹配算法考虑目标点局部邻域内的信息，匹配速度快，但精度较低；全局匹配算法通过建立一个能量函数，将立体匹配转化为能量函数的最小化问题，虽然匹配精度高，但计算复杂，实时性差，难以应用。因此，高效、准确的立体匹配算法仍然是一个很有价值的研究方向。

立体匹配大致可分为匹配代价计算、代价聚合、视差值计算和视差值精炼4个步骤[1]，绝大部分立体匹配算法包含这4个步骤或其中几个步骤。计算匹配代价是立体匹配的第一步，匹配代价的好坏对匹配精度有重要的影响。灰度/颜色差是最常用的匹配代价，这种匹配代价计算简单，速度快，但对噪声敏感，鲁棒性差。为了提高鲁棒性，学者们提出了很多不同的匹配代价计算方法，如基于Rank变换或Census变换[2]、互相关(NCC)[3]、互信息的匹配代价[4]、BT算法[5]等，这些方法属于单一的匹配代价计算方法，很难适用所有问题。文献[6- 7]将基于灰度/颜色、梯度、Census变换的匹配代价计算方法结合在一起，提高了匹配精度。文献[8- 12]使用深度学习方法，提取图像区域的高级特征用于计算匹配代价，这些特征鲁棒性好，能有效地减小相机拍照环境变化带来的不利影响。张展[13]定义了图像的内外相似度，根据内外相似度计算匹配代价，可减少误匹配点。王旭初等[14]提出了融合多尺度局部特征和深度特征的双目立体匹配算法，提高了算法对遮挡区域的适应能力。

一般来说，单个像素点的匹配代价很容易受到干扰，匹配精度不高。局部匹配算法假设一个局部邻域内，所有像素点有相同或相似的视差值，通过代价聚合，将周围像素点的匹配代价融合在一起，从而提高匹配精度。但此假设在物体的边缘位置以及倾斜平面、曲面等位置并不成立，使得最终的匹配精度不高。均值滤波是最简单的代价聚合方法，可以用于匹配精度要求不高的场合。高质量的代价聚合算法需要自适应调整滤波窗口的尺寸、形状、权重等。Yoon等[15]提出了一种自适应聚合算法，该算法的匹配精度高，匹配效果甚至可以媲美全局算法，但随着滤波窗口尺寸的增大，计算量会急剧增加，因此，出现了一些近似的算法[16- 18]，以期减少计算量，但这些近似方法会同时降低匹配精度。Hosni等[19]用导向滤波器[20]聚合匹配代价，提高了边缘位置的匹配精度，是当时匹配精度最高的代价聚合算法。局部匹配算法只考虑滤波窗口内代价信息，当目标物体纹理较弱时，聚合效果差，难以满足要求。为解决弱纹理问题，Yang[21]提出了一种基于最小生成树(MST)的非局部匹配算法，聚合匹配代价计算方法简单，速度快，但对于重复性纹理效果不好。Choi等[22]设计了一组导向滤波器和最小生成树滤波器，对于每个像素点，根据该像素点局部邻域内的信息自动选择合适的滤波器和滤波器参数。与局部匹配算法不同，全局匹配算法构造了一个能量函数，将匹配问题转化成一个能量函数最小化的问题，常用的优化方法有置信度传播(BP)[23]、图割(GC)[24]、加权树(TWR)[25]等。全局算法考虑了整幅图像的信息，匹配精度比局部匹配算法高，但计算复杂，运算时间长，极大地限制了全局匹配算法的应用。

完成代价聚合后，绝大多数匹配算法都采用“赢者通吃”(WTA)方法计算视差值，但得到的视差图仍有很多匹配错误的点，需要对视差图做进一步的校正和优化，如左右一致性检验、亚像素插值、置信度检验等，提高匹配精度。

结合物流行业的需求和特点，本文利用激光散斑增加包裹表面的纹理信息，以解决弱纹理区域“一配多”的现象，提高弱纹理区域的匹配精度。为提高匹配精度，根据激光散斑的特点，本文设计了基于梯度方向的匹配代价函数；在代价聚合过程中，将导向滤波器和半全局匹配(SGM)[4]算法串联使用，以提高算法适应倾斜平面的能力。散斑虽然能增加物体表面的纹理信息，但物体表面自身的纹理信息被过滤掉了，使得匹配算法在物体边缘位置的匹配精度不高，因此，在代价聚合之后，本文设计了相应的置信度函数，对可靠性低的视差值进行校正，以提高算法在边缘位置的匹配精度。

1 散斑立体匹配算法

弱纹理现象是物体表面有很多灰度/颜色相近的区域，在这些区域，左图中目标点在右图中存在多个对应点，对于不同的视差值，匹配代价相似，估计得到的视差值可信度不高。为了提高弱纹理区域的匹配精度，本文在物体表面投射散斑，人为地给物体表面增加纹理。散斑是激光干涉产生的随机斑点，在物体表面不同的位置，散斑的形状不同，可提高弱纹理区域不同位置的区分度。为了消除物体表面纹理信息对匹配效果的影响，本文使用红外散斑和红外相机。基于激光散斑的立体匹配算法流程图如图1所示。

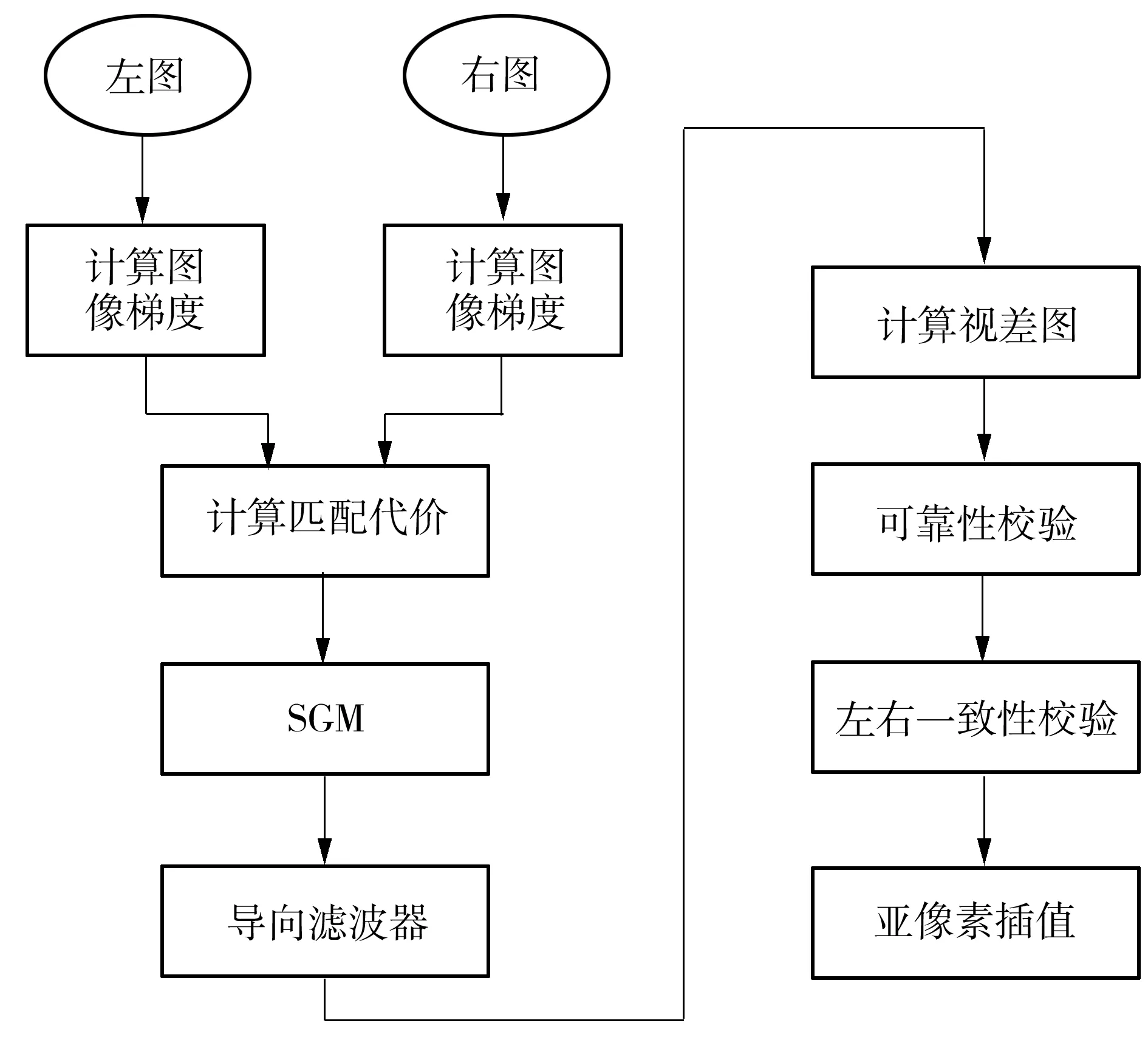
图1 基于激光散斑的立体匹配算法流程图

1.1 匹配代价计算

散斑投射到物体表面，带来了丰富的纹理信息，梯度信息也更为丰富，因此本文使用梯度计算匹配代价。尽管使用红外相机可滤掉可见光，但阳光中的红外成分仍然对散斑的亮度有影响，梯度大小因此也受到影响。相比于梯度大小，梯度方向受光照的影响小，因此本文使用梯度方向来计算匹配代价，即

(1)

式中，θgd,L、θgd,R分别是左图和右图的梯度方向角，p是左图中的点，pd是p在右图中视差为d的匹配点。

在时域对图像做卷积可以很容易得到每个像素的梯度，但梯度方向的计算比较耗时。两个向量夹角的余弦值可以通过向量的內积获得，计算简单，因此本文使用梯度夹角的余弦值来计算匹配代价。在双目视觉中，由于左右两个相机的拍摄位置不同，同一个目标点在左右两幅图像中的灰度/颜色会发生变化，好的代价函数要能够抑制这种变化。通常，为了消除明显的错误匹配，大多数匹配代价函数都会使用截断函数(如BT等)。余弦函数能很好地满足这两个需求。

1.2 代价聚合

采用式(1)计算匹配代价时仅仅考虑了像素点自身的梯度，容易受到干扰，造成大量的误匹配。代价聚合假设一个局部邻域内的像素点有相同或相似的视差值，将邻域内所有像素点的匹配代价聚合起来，可以抑制噪声的影响，减少误匹配。均值滤波是最简单的聚合方法，但在物体的边缘聚合效果差，可应用于匹配精度要求不高的场合。导向滤波器[20]能够保存物体的边缘信息，匹配精度高，计算时间受邻域尺寸的影响小，能够满足实时性的要求。本文使用导向滤波器进行代价聚合，即

(2)

εU)-1(Ik-μs)]

(3)

式中：R为参考图，因要计算左图的视差图，因此使用左图作为参考图；Ip、Ik分别为参考图在p、k点的颜色值；s为包含p、k点的窗口ws的中心，窗口大小为w×w；μs、σs分别为窗口ws内所有像素点颜色值的均值和方差；U为单位矩阵；ε为平滑参数;Cs(k,d)为使用SGM算法聚合后的匹配代价。

导向滤波器在聚合匹配代价时，对窗口邻域内不同像素的匹配代价赋予不同的权重，p、k点的颜色/灰度值接近时赋予较大的权重。在边缘位置，如果p、k点属于不同物体，颜色/灰度值差别大，则赋予的权重小。因此导向滤波器可以保留图像的边缘信息。然而，对于曲面和斜面，同一物体表面的像素点灰度值/颜色接近，但是视差值不同，邻域窗口的尺寸越大，这种差别越大，导向滤波器的效果越差。为了弥补这一不足，本文在导向滤波器的前端增加了一个SGM[4]的代价聚合，与全局匹配算法类似，半全局匹配算法首先定义一个能量函数E(d)，将求视差值的问题转化成一个能量函数最小化的问题：

(4)

式中：Np为p的邻域；P1、P2为惩罚因子，且P2>P1；T(·)为条件函数，当条件为真时函数值为1，否则为0。式(4)的第一项为数据项，代表每个像素点的匹配代价；第二项和第三项为平滑项，使相邻像素的视差值尽可能相同，小的惩罚因子P1使得能量函数能够适应曲面或斜面带来的影响。能量函数(4)的最小化是一个NP完全问题，常用的近似方法如BP、 GC等方法的计算量非常大，难以满足实时性要求。SGM将能量函数的优化问题转化成多个一维动态规划，即

(5)

Lr(p,d)=C(p,d)+min(Lr(p,d),

Lr(p-r,d-1)+P1,Lr(p-r,d+1)+P1,

(6)

式中，r为路径数，文献[4]建议使用16条路径。本文中SGM是匹配代价聚合中的一个步骤，只使用4条路径，从而减少计算量。

1.3 视差值计算

匹配代价聚合后，对于每个像素点，使用WTA方法计算最优视差值，即

(7)

为了提高匹配精度，本文还需要计算右图的视差图，计算方法与左图的相同。得到右图的视差图后可以进行左右一致性校验，检测遮挡和误匹配，提高边缘位置的匹配精度。

1.4 视差图后处理

使用聚合后的匹配代价计算的视差值仍然会存在很多匹配错误点，需要做进一步的处理来提高匹配精度。

(8)

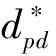
(9)

则对视差值进行插值，即

(10)

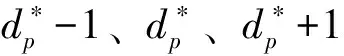
1.5 算法复杂度分析

为了使算法满足实际应用中的实时性要求，本文使用梯度方向角的差值来计算匹配代价，因为直接使用梯度方向计算量会比较大，故文中使用梯度角的余弦值代替，对每个像素点只需进行两次(x方向和y方向)减法、两次加法即可得到梯度，归一化之后对每个待匹配点进行一次乘法和减法即可得到匹配代价，计算复杂度为O(Nd)，其中N为像素点的个数，d为视差值的范围。在代价聚合时，本文将导向滤波器和SGM算法串联起来，导向滤波器通过串联的均值滤波以及滤波窗口内的方差即可达到双边滤波器的效果，其计算复杂度为O(N)。导向滤波器计算量的详细分析见参考文献[20]。半全局匹配SGM算法通过将多路径的动态优化过程分解成多个单路径的优化过程，极大地减少了计算量，计算复杂度为O(Nd)，具体分析见参考文献[4]。本文使用的SGM算法的复杂度为O(Nd)，而且可以通过并行计算进行加速，因此可以达到较好的实时性。

2 实验结果分析与讨论

2.1 实验结果分析

本文使用激光散斑给物体表面增加纹理，可以提高匹配算法对弱纹理区域的处理能力。目前立体匹配的公共数据集中没有带散斑的验证图像，本文使用自行拍摄的图像来验证算法的有效性，算法中参数设定如下：{w,ε,P1,P2,}={19,0.01,0.3,0.6,0.2}。实验中使用130万像素的相机，物体的高度变化在50～1 000 mm，图像处理器(GPU)加速之后，测量时间大约为0.7 s，基本达到实时测量的要求。

在匹配之前，首先对左右图像进行校正，使得左右两个相机的图像平面共面行对准，即左右两个相机的图像平面在同一个平面上，并且同一个目标点在左右两个相机的投影点行坐标相同，这样匹配算法只需要在一个水平直线上寻找匹配点，大大减少计算量。本文使用Bougeut方法对左右图像进行校正。这种方法同时旋转左右图像，使得目标点的投影畸变最小。图像校正之后利用匹配算法得到视差图。

图2(a)所示是待匹配的图像(将一个测量尺放在测试台面上，散斑投射在物体表面和测量台面)，代价聚合之后得到的视差图如图2(b)所示。由于工作台面以外的位置几乎看不到散斑，因此很难正确估计这些位置的视差值，视差值的可信度低，而且由于遮挡的问题，测量尺左侧部分的视差值估计也不准确。对视差图进行后处理之后的视差图见图2(c)，从图中可以看出，经过置信度检验后，测量台面以外的区域的视差值都被置0，而台面和物体的视差值很好地被保留了下来。为了进一步检验匹配效果，本文将原图(绿色)和估计得到的视差图(红色)叠加显示，如图2(d)所示，原图为绿色，视差图为红色，重叠的部分为黄色，将对比图局部放大，可以看到测量尺视差图左侧边缘位置与原图边缘位置基本重合，验证了本文算法能很好地适应物体边缘带来的视差不连续问题。

为了定量评价本文提出的算法，利用得到的视差图重构物体的三维坐标，计算物体的尺寸，对比物体的实际尺寸与测量尺寸，通过测量精度衡量算法的性能。实验中选择了多个不同尺寸的物体，以不同姿态放置在台面的不同位置进行15次测量。

图2 本文算法的实验结果Fig.2 Experimental results of the proposed algorithm

图3 倾斜平面的视差图Fig.3 Disparity map of slant plane

通过双目相机测量物体的实际尺寸时，还需要对相机进行标定和校正。本文采用棋盘格标定相机的内外参数，在工作区域内，将棋盘格摆放在不同的位置并以不同的姿态拍摄校正图像，使用张正友标定法[26]进行标定。本文使用红外相机拍摄图像，在标定过程中，如果安装环境中有自然光，只需调大相机的曝光时间，即可得到清晰的标定图像；如果相机安装在自然光很弱或者没有自然光的地方，则使用红外光源进行补光，完成相机标定。标定完成后，根据相机的内外参数及视差图重构物体的三维信息，获得物体的三维尺寸。

实验中，使用卷尺在物体的不同位置测量3次，以最大值为物体的真实尺寸；利用视差图重构出的三维尺寸，本文用最大外接矩形的尺寸表示测量值。不同物体的实测结果如表1所示。从表中可以看出：深度方向最大测量误差比较小，测量误差在±3%以内，说明本文算法能比较准确地估计出物体的视差值；立体匹配中的遮挡问题使得很难准确估计物体的边缘位置，导致台面方向的测量误差(X、Y轴误差)相对深度方向大了很多，达到±5%左右；相对于凳子、测量板等物体，纸箱材质比较软，容易发生形变，导致的测量误差也会更大一些。

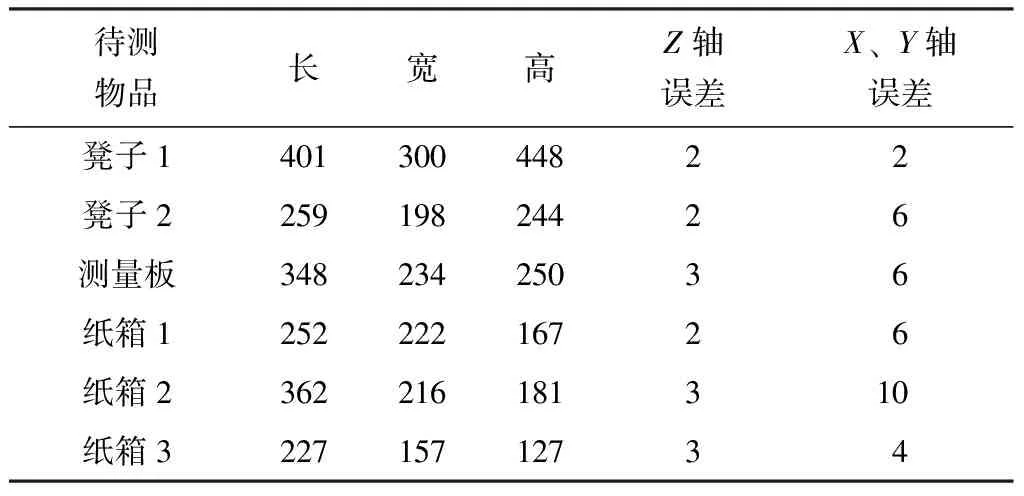
表1 不同物体的实测结果Table 1 Measured results of different objects mm

2.2 实验结果讨论

本文利用激光散斑增加物体表面的纹理，可以有效降低算法的复杂度，散斑纹理简单，因此简单的匹配代价计算方法就可以取得比较好的效果，与基于灰度/颜色差、梯度的匹配代价相比，基于梯度方向的匹配代价在遮挡区域的可靠性更高。但散斑也会带来一些不利因素，如本文使用红外激光散斑和红外相机，会滤除物体本身的纹理信息，增加了遮挡区域的匹配难度。一般情况下，散斑投射器安装在物体正上方，由于遮挡问题，物体边缘位置没有散斑，如图4所示，箱子上侧边缘和右侧边缘没有散斑，增加了边缘位置的匹配难度。另外，如果箱子放置在测量台面的边缘位置，相机会拍到箱子的侧面，侧面散斑效果差，也会降低匹配精度。

图4 散斑效果不理想的图像Fig.4 Image with low quality speckles

在实际测量中还发现一些其他问题，例如物体放置在测量台面中央时测量结果更准确，垂直于视差方向的尺寸测量比较准确，而平行于视差方向的尺寸由于遮挡导致测量结果偏大。这些问题将在未来做进一步的研究。

3 结论

本文通过激光散斑增加物体表面的纹理信息，提高了匹配精度，特别是对于弱纹理区域。根据散斑带来的丰富纹理信息，本文使用梯度方向计算匹配代价，有效减小了光照变化带来的不利影响，提高了匹配精度。代价聚合时，为了更好适应物体边缘及斜面带来的影响，本文融合了导向滤波器和SGM算法，提高了算法在这些区域的匹配精度。最后根据聚合后的匹配代价，本文提出了一种可靠性检验方法，有效地减少了遮挡带来的错误匹配。本文根据相机的内外参数重构物体的三维信息，利用测量精度衡量算法的性能。在实验过程中，对于尺寸不易发生形变的物体，测量精度可以在±3%以内；对于材质较软、容易发生形变的物体，测量精度也可以达到±5%；在ThinkPadX250平台上运行，测量时间大约0.7 s。本文提出的算法已经在某物流公司调试，基本满足客户的需求，预计可以带来可观的经济效益。