高中数学习题课的选题策略研究

芮雪妮

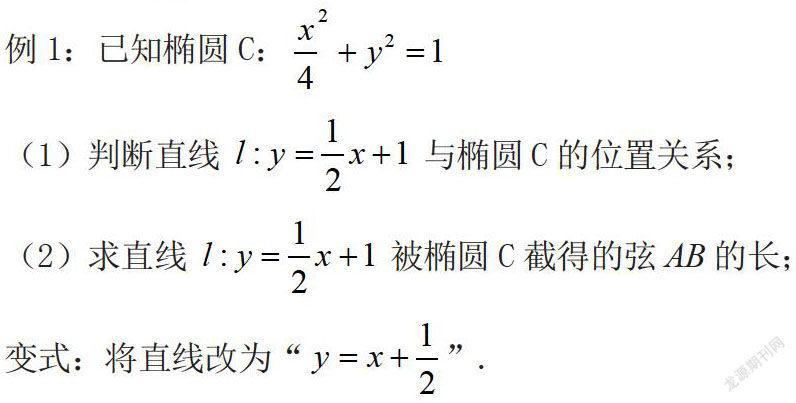
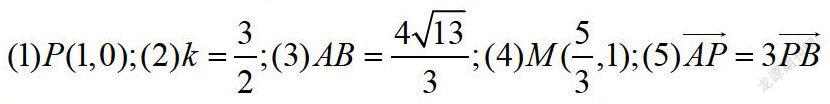
摘 要：习题课，被定义为“学生在教师面对面的指导下，对指定题目进行解题作业的一种教学形式”。这种教学形式在数学教学中尤为重要。它能够帮助学生更好地了解我们学习的知识点应该怎么用，用在哪儿，从而总结经验，提高解题效率。要上好一节习题课要做到课前精心准备，课堂精彩讲授，课后跟踪反馈。而本文将结合本人教学经历与见闻，着重谈一谈习题课课前准备过程中的选题策略，希望对广大数学教师有所帮助。

关键词：数学习题课;主题明确;典型性;递进原则;巩固性原則

数学教学中，教师常常会花一整节课去研究习题，这些习题旨在训练学生学会运用所学知识，从而帮助学生更加深层次的理解新知，并达到能利用知识解决一类问题的程度，像这样的课通常称为习题课。

习题课在数学教学中是非常有必要的。数学是一门基础学科，它作为工具，是一切科学的基础，所以我们要会用数学知识解决问题。而当下，许多学生都有这样的一个困境，听知识点一听就会，但做题一做就懵，自己也说不明白是哪里不懂，很难从题目中提取到关键信息，也无法迅速将已有的认知和问题准确联系起来，导致做题常常会走偏，甚至都无从下笔，这种现象在高中特别常见。而要解决这样的问题，就需要教师通过习题教学使学生形成解决一类问题的方式方法，或者说是掌握解决一类问题的“套路”，从而培养学生应用知识去分析问题、解决问题的能力。

正因为习题课十分必要，所以备课阶段“如何选题”“选什么题”就显得尤为重要。选择合适的题目，能够让学生在充分的练习中掌握方法。那么本文就将以选题问题作为切入点，结合笔者课堂教学经验，探讨习题课备课阶段选题的几项原则。

一、整节课主题要明确

数学教学中有这样一类老师，他们很辛苦，面对茫茫题海，他们无法抉择，生怕学生会错过任何一道题。一节习题课，他们可能会拿出四五道，甚至更多道“好题”，这些题目包含的方法多种多样，都很精彩。但解决完后呢？不能说所有学生都毫无所得，但对于相当一部分同学，尤其是基础稍薄弱，解题能力本就欠缺的同学来说，他们一节课也就会做这几道题了，换一个情境，该不会的还是不会。

我认为一节习题课要有一个主线：这节课你想让学生学什么？是想让学生掌握一类问题的解法;又或是让学生在训练中规范书写;再或是让学生在习题教学中感受数学思想，如以算代证思想、数形结合思想……而选题自然也要符合主线，不能走题，东一榔头西一棒，让学生摸不着头脑。既然是课，就要有所得，新授课得的是知识，习题课得的是方法。

二、切入题选择要具有典型性

确定好主题后，就要根据主题选择适当的例题，所谓适当，就是要典型，尤其是切入题，也就是首道例题。

在我们选择切入题时，教师应避免以下问题出现：

（1）题目综合性太强。希望一道题能包含多种思想，既能体现本节课主题，又能包含其他知识。自认为选题很完美，能让孩子学到很多，殊不知冲淡了主题。教师很可能需花大量时间在复习旧知上，但对于基础薄弱的孩子来说，短暂的复习并没有什么用。并且对于你想让他掌握的方法他也无心去学了。

（2）计算量过大。运算量大无疑就是难度加大，学生在大量运算中，关注点会发生偏离，忘了题目本身想让我们得到的思想方法，这是毫无必要的。尤其作为首道例题，一上来就给学生一个下马威，下面就很难进行了。

（3）解题过程绕弯太多。题目不难，但过程太绕，同样也会耗费学生大量精力，不适合课堂讲解，也是教师给自己找“麻烦”。

综上所述，我们所选择的切入题需要能够直接反映主题，它可以是一类数学题的代表，或是体现一类数学思想的代表。题海无边，当我们掌握了方法，无疑是乘上了一条能在题海中自由游行的船，让学生事半功倍，真正学会应用知识。同时，切入题的过程、计算都不需要太过复杂，主要是让学生掌握方法，而不是为难学生。

下面是本人在“直线与椭圆位置关系”教学中选择的切入题，以及选题分析。

本节课主题是探讨直线与椭圆位置关系，并且学会应用代数法解决位置关系相关问题，尤其是相交问题。针对这样的主题，我设计了切入题，它包含三个小题。

第（1）小题，旨在教会学生判断直线椭圆位置关系的一般方法——联立求。

三、例题间须符合递进原则

一节习题课不只有一道例题，例题间，笔者认为：应遵循递进原则，层层深入，由浅入深。我们备一节习题课其实就像写一篇文章，要有一条逻辑线，符合主题的情况下，题与题之间也需要关联，且层层递进，能让学生在掌握上一题的基础上，自然而然、顺理成章地过渡到下一题的解题思路中去。

例如上文提到的“直线与椭圆位置关系”一课中，我选择的例2是：

这道题较例1难度有所提升，已知弦长求直线，是一个典型的含参问题。但是方法是类似的，通过联立、设而不求，韦达定理，用参数表示出弦长，构造等式，求出参数b。通过这样一个递进，学生能够更加深层次的理解弦长公式。同时这样的含参问题，或者说是待定系数求直线的方法正是解析几何常见的求解方程方法，这也与之前学习的内容巧妙的结合起来了。

紧接着告诉学生，其实不只是求弦长，联立后利用韦达定理其实是直线与圆锥曲线问题的通法，过渡到下一道例题。

这道题中要求直线方程，可以待定系数，设直线斜率，接下来还是固定套路求解。这里完全可以让学生探讨出思路后展示求解过程，充分体现出学生的主观能动性。完成讲解后，再提问：“这道题是否还有其他解法呢？”事实上根据这道题“中点”条件的特殊性，我们还可以采用点差法求解，充分体现出“一题多解”在数学题中的应用，并进行总结思考：什么时候可以用点差法呢？培养学生发散思维。

也就是说所谓递进原则，是由浅入深，由单一知识到综合应用，由多题一解的深刻性走向一题多解的发散性的过程。这样的过程也符合教育心理学的要求，顺应学生的心理发展，更利于学生接受。

四、课后反馈题符合巩固性原则

在课堂上处理习题的时间是有限的，一节课四十五分钟，能将思想方法总结到位已实属不易，要想真正掌握，还离不开课后习题的选择。而课后的反馈题必须符合巩固性原则。巩固性原则是教学原则之一，要求学生所学的知识、技能达到牢固和熟练的程度，能够在需要的时候及时地、准确地再现出来。课后反馈题就是让我们巩固，从而真正掌握的一个过程，所以题目要能很好地反映这节课的重点，而不是一堆题型大锅炖。

曾有幸听过一节关于“直线与抛物线”的习题课。

课上例题：已知抛物线y2=3x的焦点为F，过点P作直线l交抛物线于A、B两点，线段AB中点为M，

课上老师将（1）（2）作为条件，可以推出（3）（4）（5），并让同学思考了：可否选择（2）（3），推出（1）（4）（5）？最后得出结论，实际上只要知道任两个条件都可以推出其他结论。课后反馈题目是让学生尝试选择不同的选项作为已知条件，自己编题证明。充分的发挥了学生的主观能动性。

这节课给了我很多启发，学生课后练习如果仅仅是机械性的重复，甚至是大量重复，就很难做到灵活变通。而课上时间有限，课下同学之间交流探讨的时间是很长的，不妨在可行的情况下，通过这样开放性的题目让学生巩固的同时，积极思考，合作交流，相信对学生掌握方法会很有价值。最后反馈练习中教师可以根据学生层次差异设置一两道“选做题”。尊重学生之间的个体差异，拓展学生的视野，增强学生的学习兴趣。

习题课的教学值得探讨和深思的还有很多很多，本文也仅能通过短短篇幅简略地表达我的一些思考。真正在教学中，要想让学生一节习题课上的有价值，不仅仅要重视选题，选完题如何针对不同层次学生去讲？如何将学生讲明白？……还需要更多的实践总结。总之，我们数学教师要在充分理解数学课程标准的基础上，将培养学生核心素养作为出发点，研究每一堂课，包括习题课。要知道，在实际数学教学过程中，习题课所占比重是非常大的。要努力克服传统习题课的弊端，要使劳动有价值。“题海无边，回头是岸”，我们要多思考，多研究，提高教学质量。

参考文献

[1]韋宏，张桂玉，黄美玲.数学习题课教学的弊端与创新[J].智库时代，2019，No.201（33）：221-222.

[2]刘梨凤.初中数学习题课变式教学的几点建议[J].新智慧，2019，（04）：108.

[3]王登，乔世红.习题课教学策略及注意事项[J].新课程（下），2019，No.471（01）：126.

[4]李银耀.新课改条件下如何上好数学习题课[J].考试周刊，2010，（30）：14-15.

[5]任云岗.数学习题课教学的有效性探析[J].读与写（教育教学刊），2010，v.7（01）：172.

[6]张景中，张奠宙.数学习题教学研究[M].上海：教育出版社.2010