基于WEA优化神经网络的桥梁车载识别

陈修辉，赵恒博，邱 宁

(青岛理工大学 琴岛学院，山东 青岛 266106)

桥梁在现代交通中的重要性不言而喻，而桥梁的健康监测是桥梁规划设计、安全性评估、耐久性估测、日常性维护等的重要依据[1]。桥梁健康监测中极为重要的一个内容便是桥梁的车载识别，它是健康监测过程中必不可少的环节。由桥梁的应变、挠度等响应来识别桥梁车载的方法已有很多种，包括时域法、频时域法、拟合法、智能方法等。ZHU X Q等采用时域法识别桥梁动载[2]。Law S S等采用频时域法识别桥梁动载[3]。李忠献等分别采用梁格法和BP神经网络识别桥梁动载[4-5]。张渔勇等采用样条函数识别桥梁多轴车载[6]。WU S Q等采用随机有限元模型识别桥梁动载[7]。王蕾等采用荷载形函数识别大跨桥梁动载[8]。陈修辉等采用神经网络识别悬索桥动载[9]。陶兴旺等采用神经网络识别斜拉桥车载[10]。智能方法是近年来最为热点的方法之一，该方法的关键是确定神经网络结构，而神经网络结构中最为重要的环节就是网络参数的给出。但在寻优网络参数过程中，往往会出现鲁棒性差、收敛速度慢、易陷入局部早熟等缺陷。针对这些缺陷，本文在基本的灰狼优化算法基础上提出头狼效应算法，以此优化神经网络参数，并用于桥梁车载的识别，数值模拟结果证明该方法具有很好的识别能力。

1 基于神经网络的桥梁车载识别

基于神经网络进行桥梁车载识别是利用神经网络的自适应模式识别技术进行识别，其中的关键是神经网络结构确定。神经网络结构的确定主要包括三个方面：拓扑结构、样本选取与处置、网络参数，其中最难确定的方面是网络参数。本文中神经网络的拓扑结构选用3层网络，假设输入层单元数为i，则隐含层单元数选为2i+1，输出层单元数由输出向量维数确定。以车载作用下的桥梁响应作为神经网络的输入向量，以车载大小等作为神经网络的输出向量，组成样本，构建样本库，且对样本进行归一化处置。神经网络的参数则由本文提出的头狼效应算法确定。

2 头狼效应算法

灰狼优化算法[11-12](Grey Wolf Optimization, GWO)是由Mirjalili S等于2014年提出的一种新型的智能优化算法，它模拟了自然界中灰狼的围捕猎物行为和等级制度，主要包括跟随、围捕、攻击等过程。该算法具有参数少、原理简单、全局搜索能力强等特点，因此在工控系统入侵检测[13]、物流配送路径规划[14]等众多问题中得到广泛应用。但基本的灰狼优化算法存在着容易陷入局部早熟、后期收敛速度慢，尤其对高维复杂问题优化精度不够高等问题。为解决此类问题，本文提出一种在基本的灰狼优化算法基础之上改进而来的头狼效应算法(Wolf Effect Algorithm, WEA)。

头狼效应具有很显著的生物学意义。狼喜欢集体行动，而狼群中必有个头狼，它是狼群中最优秀的一个，集中了狼的最优秀品质，是狼群的核心，具有绝对的领导地位。当狼群遇到困难或需要捕食时，头狼会指挥狼群、分配狼群进行行动，从而取得胜利。当由多支狼群组成更大的狼群时，则在多个头狼之中必有一个头狼的头，即狼王。大的狼群在狼王的带领下，呼啸山野，出没草原，所到之处，披靡无敌，这就是头狼效应。

在基本的灰狼优化算法(GWO)中，先找到当前适应度值最优的三个解，并把这三个解分别称之为第一最优解记为α狼、第二最优解记为β狼，第三最优解记为δ狼，剩余的狼记为ω狼。每个ω狼都会评估自己与三个最优狼之间的距离，跟随它们围捕猎物并最终攻击猎物。ω狼在跟随、围捕猎物时，需要同时跟随α狼、β狼和δ狼，根据这三个最优狼的位置更新自身的位置，跟随速度即算法中的收敛速度必然较慢。但若单纯的跟随最优狼即α狼，又可能出现跟随偏差陷入局部而无法跳出即陷入局部早熟的情况。为更好的利用最优狼的信息，同时又加快收敛速度，故而提出头狼效应算法(WEA)。

首先构筑一大的狼群，而整个大的狼群由S个小的子狼群组成，子狼群之间彼此独立。在每个子狼群中，根据每个狼的适应度值大小，选取适应度值最优的狼称之为头狼记为αi狼(i=1,2,3,…,S)，剩余的狼记为ωi狼(i=1,2,3,…,S)。在ωi狼中，适应度值最差的1/8狼个体直接淘汰，并用随机产生的狼个体替代，既保证了每个子狼群中狼群规模的稳定，又保证了子狼群中狼个体的多样性。其余的狼个体均跟随头狼进行位置的更新，实现对猎物的围捕，围捕行动可采用如下公式表示：

Xi(t+1)=Xαi(t)-Ai·Di

(1)

Ai=2airi1-ai

具体地说，尽管一线教师普遍十分重视课例，包括教学观摩与教学研究，但是，这方面的活动往往又满足于如何能由相关课例、特别是优秀教师的课例获得某些可资直接借鉴特别是简单模仿的经验或教学设计，即如某一特殊情境的创设，某些特殊教学工具的开发等．另外，就自身教学工作的总结与反思而言，往往也只是一种“就事论事”“亡羊补牢”的工作，即只是集中于教学中的某些细节，特别是不足之处，如教学中某个问题的设计可以如何改进，学生在这一内容的学习过程中为什么出现某种错误等．正因为此，尽管此类工作确实有益于教学的改进，但却很难说具有更普遍的作用，包括如何能够通过此类活动更有效地促进自已的专业成长．

(2)

(3)

Di=|CiXαi(t)-Xi(t)|

(4)

Ci=2ri2

(5)

其中，i=1,2,3,…,S；Xi(t)表示第i个子狼群中第t代狼个体的位置；Xαi(t)表示第i个子狼群中第t代头狼的位置；Ai、Di、Ci表示第i个子狼群的收敛系数；ri1、ri2表示第i个子狼群中在[0,1]区间内的随机数；Timax表示第i个子狼群的最大迭代次数。每个子狼群分别单独实现对猎物的围捕。待S个子狼群均完成对猎物的围捕后，即每个子狼群均达到最大迭代次数，便可得到S个最为优秀的头狼。由这S个子狼群的头狼再组成一新的更高一级层面的高层狼群。根据高层狼群中S个头狼适应度值的大小，选取适应度值最优的头狼称之为狼王记为α狼，其余的头狼均跟随狼王进行位置的更新，实现对猎物的围捕，此时的围捕行动仍采用类似前述公式(1)～(5)表示。最后，狼群体跟随头狼，头狼再跟随狼王完成对猎物的围捕、攻击，从而实现对函数的逼近，此即为头狼效应算法(WEA)。

头狼效应算法(WEA)的步骤如下：

步骤1 设置参数：子狼群个数S，每个子狼群的狼个体数N，最大迭代次数Tmax，狼个体的维度d，狼个体搜索空间上、下界Ub、Lb。

步骤2 初始化：狼个体位置X，随机数r1、r2。

步骤3 子狼群按适应度值优选出头狼，其余狼个体按公式1～5完成位置更新。

步骤5 高层狼群按适应度值选出狼王，头狼按公式1～5完成位置更新。

步骤6 判断高层狼群是否达到最大迭代次数或狼王是否满足终止条件；若是，则输出狼王作为最优解；若否，则返回步骤5。

为考察头狼效应算法(WEA)的有效性能，选取5个典型的测试函数进行数值对比实验，选取的5个典型测试函数如表1所示：

表1 测试函数

借助5个测试函数，对头狼效应算法(WEA)与灰狼优化算法(GWO)进行比较，算法中的参数设置均相同，最大迭代次数均为500代，每个测试函数的维度数均取为30。为避免算法初始化等对结果可能造成的偶然性，每种算法均独立运算20次，并取最优结果的平均值。两种算法的对比结果如表2所示。对比结果表明，与灰狼优化算法(GWO)相比头狼效应算法(WEA)确实具有更好的寻优能力。

表2 测试函数对比结果

3 车载识别的数值模拟

模拟实验的运行环境为Intel Core i3-9100处理器，运行内存为8Gb，Windows10 64位操作系统。实验中所用的软件分别为ANSYS13.0和MATLAB7.0。桥梁的响应由ANSYS13.0数值计算得出，头狼效应算法的网络参数优化以及神经网络的车载识别均由MATLAB7.0软件实现。

将桥梁结构视为两端自由两端简支的正交异性板模型，将桥梁结构上的车辆轮载视为固定距离的四个时变集中力，且恰好沿正交异性板从左向右匀速直线运动，如图1所示。板的相关参数分别为：长a=45m，宽b=15m，高h=0.2m，弹性模量Ex=41GPa、Ey=29GPa，密度ρ=3000kg/m3，泊松比μ=0.33。其中，Ex、Ey分别表示板在x、y方向的弹性模量。假设四个时变集中力分别为(单位为N)：

图1 车载沿正交异性板运动时的示意图

f1=3000(1-0.1sin(20πt))

f2=3000(1+0.1sin(20πt))

f3=3500(1+0.1sin(20πt))

f4=3500(1-0.1sin(20πt))

从左向右看，f1和f2分别代表车辆前轮右边和左边的轮载，f3和f4分别代表车辆后轮右边和左边的轮载，车辆的轴距为d1=2700mm，轮距为d2=1500mm，运行速度为v=30m/s，车辆行驶路线为右轮距板右边距离为D=6.75m。故，对四个时变力而言，

在正交异性板模型上，选取坐标分别为(11.25,5)，(11.25,10)，(22.5,5)，(22.5,10)，(33.75,5)，(33.75,10)的六个点。以此六点作为响应数据采样点采样板的挠度响应，采样的频率为100Hz，并用ANSYS数值计算得到的挠度响应代替实测的挠度响应。将数值计算的挠度响应作为神经网络的输入向量，将代表车载的时变力作为神经网络的输出向量，组建构成测试用样本库，以待后用。

再假设车辆轮载分别为：

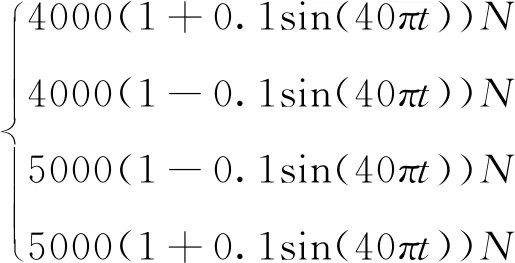
各力代表的轮载属性与前述均相同。同样的六个采样点，同样的采样频率，将相应的数据信息组建构成训练用样本，用以训练神经网络，确定神经网络结构。

神经网络模型选用最简单的BP神经网络，该神经网络输入层单元数为6，隐含层单元数为13，输出层单元数为4，输入层与隐含层之间选用S型传递函数，隐含层与输出层之间选用线性型传递函数，神经网络参数共(6×13+13+4×13+4=147)147个。分别应用灰狼优化算法(GWO)和本文提出的头狼效应算法(WEA)优化神经网络的参数，训练神经网络。在两算法中，狼个体的维数均应为147，最大迭代次数均为300代。其中，灰狼优化算法(GWO)中，狼群的狼个体数为1600个；头狼效应算法(WEA)中，子狼群个数为40个，每个子狼群的狼个体数为40个。对于训练完成的神经网络，将测试用样本带入其中，即可得到车辆轮载的识别结果，如图2～图5所示。

图3 车载左前轮识别图

图4 车载右后轮识别图

图5 车载左后轮识别图

4 结论

由识别结果的图2～图5可知，相对灰狼优化算法(GWO)，利用头狼效应算法(WEA)优化神经网络参数，其识别结果要好很多，可以得到更好的识别精度，为智能健康监测系统的建立奠定理论基础。虽然已经得到较好的识别精度，但本文所选用的神经网络数据均为计算机模拟得到，对于工程实际桥梁的车辆轮载识别还需进一步研究。